Высшая проба 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дан выпуклый многогранник. Разделим длину каждого ребра на сумму длин остальных ребер и вычислим сумму полученных дробей.
Докажите, что полученная сумма меньше
Источники:
Подсказка 1
В плоскости мы умеем давать оценки на какие-то суммы длин. Но сейчас мы работаем в пространстве, значит, нужно найти плоскости!
Подсказка 2
Рассмотрите многоугольники, в которые входит конкретное ребро. Какие оценки на длину этого ребра можно в них сделать?
Подсказка 3
Воспользуйтесь неравенством многоугольника для каждого ребра!
Подсказка 4
Для каждого ребра имеется как минимум два непересекающихся набора других рёбер, длины которых в сумме больше, чем длина этого ребра. Тогда можно сделать оценку на длину каждого ребра многогранника!
Подсказка 5
Длина ребра многогранника всегда меньше, чем L/3, где L — сумма длин рёбер многогранника.
Обозначим за длины ребер многогранника, а за
— сумму длин всех ребер многогранника. Каждое ребро многогранника
входит в две грани, которые являются многоугольниками. Отсюда следует, что для каждого ребра имеется как минимум два
непересекающихся набора других ребер, длины которых в сумме больше, чем длина этого ребра (по неравенству многоугольника). Это
значит, что длина каждого ребра многогранника всегда меньше, чем
а значит, сумма длин всех ребер, кроме одного, всегда больше,
чем
Теперь запишем сумму дробей из условия и заменим в каждой дроби знаменатель на
— от этого сумма строго увеличится,
но станет равной
Ошибка.
Попробуйте повторить позже
Многочлен со старшим коэффициентом
имеет только целые коэффициенты, среди которых есть отрицательные. Обязательно ли
многочлен
имеет хотя бы один отрицательный коэффициент?
Источники:
Подсказка 1
Это задача — конструктив. Значит, ответ — необязательно, и нужно лишь привести пример многочлена.
Подсказка 2
Попробуйте реализовать следующую идею. Придумайте приведенный многочлен с одним отрицательным коэффициентом такой, что его куб и квадрат имеют только положительные коэффициенты. Тогда и 2025 степень тоже будет только с положительными.
Подсказка 3
Вероятно, вы попытались придумать такой многочлен 1, 2, 3 степени и потерпели неудачу. Как насчёт того, чтобы попробовать придумать многочлен 4 степени?
Покажем несколько примеров приведенных многочленов с целыми коэффициентами, среди которых есть отрицательные, у которых -я
степень не имеет отрицательных коэффициентов.
Пример 1. Рассмотрим многочлен
где — достаточно большое натуральное число (на самом деле, достаточно взять
Проверим, что
и
имеют
только положительные коэффициенты:
Теперь положим Этот многочлен приведённый, имеет только целые коэффициенты и один отрицательный. Покажем,
что
и
тоже имеют только неотрицательные коэффициенты:
Единственный отрицательный коэффициент в этой сумме есть только у при
он равен
но коэффициент при
у
равен
поэтому вся сумма не имеет отрицательных коэффициентов.
Единственный отрицательный коэффициент в этой сумме есть только у при
и он равен
но коэффициент при
уже в
равен
поэтому вся сумма гарантированно не имеет отрицательных коэффициентов.
Поэтому и
не имеют отрицательных коэффициентов, а значит, и
для всех больших
не имеет
отрицательных коэффициентов, так как любое число, большее
представимо в виде суммы двоек и троек.
Идея этого примера такова: рассмотрим многочлен Его любая степень имеет положительные коэффициенты (нет
нулевых). “Пошевелив” (на данный момент нулевой) коэффициент при
в отрицательную сторону мы получим многочлен, коэффициенты
степеней которого «мало» отличаются от коэффициентов тех же степеней многочлена
так как коэффициенты его степеней
являются непрерывными функциями от параметра
поэтому при малом
степени многочлена
будут иметь только положительные коэффициенты. На основе этого легко построить приведенный
целочисленный многочлен, у которого все степени имеют только положительные коэффициенты. Аналогично подходит многочлен
и его шевеления
для всех
при
тогда
дает нам нужный пример многочлена имеющий произвольную степень
______________________________________________________________________________________________________________________________________________________
Пример 2. Рассмотрим
Тогда многочлены и
тоже имеют только положительные коэффициенты, а значит, и для всех
многочлен
будет иметь только положительные коэффициенты. Аналогичные примеры можно построить для любой степени, не меньшей
(почти все коэффициенты равны
В этом примере минимальная степень
многочлена равна
______________________________________________________________________________________________________________________________________________________
Пример 3. Пусть Рассмотрим
(все коэффициенты, кроме одного, равны Тогда
и
не имеют отрицательных коэффициентов, а значит, и для всех
многочлен
не будет иметь отрицательных коэффициентов. В этом примере модули коэффициентов не превосходят
______________________________________________________________________________________________________________________________________________________
Замечание 1. Данные примеры показывают, что для любого существует приведённый целочисленный многочлен степени
с
отрицательным коэффициентом, старшие степени которого не имеют отрицательных коэффициентов. Можно доказать, что если
квадратичный или кубический многочлен имеет отрицательные коэффициенты, то его степени тоже будут иметь отрицательные
коэффициенты.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание 2. Для всякого можно построить целочисленный приведенный многочлен
степени которого вплоть до
имеют отрицательные коэффициенты, а начиная с
не имеют отрицательных коэффициентов.
Не обязательно
Ошибка.
Попробуйте повторить позже
Дан шестиугольник в котором
Докажите, что
Источники:
Подсказка 1
Вспомним условие на сумму углов в n-угольнике. Чем нам это может помочь? Для каких углов получается выразить величины?
Подсказка 2
Обратим внимание на четырёхугольник, образованный точками A, B, D, E. Какие свойства есть у вписанного четырёхугольника? Что ещё можно сказать про этот четырёхугольник?
Подсказка 3
Попробуем применить симметрию относительно середины отрезков BD и AE – какие новые точки и фигуры при этом получаются?
Подсказка 4
Рассмотрим полученные после отражения точки и параллелограммы. Какие стороны оказываются параллельны, а какие равны по длине? Можно ли использовать равенство углов и расстояний до прямой, чтобы сделать вывод о равенстве боковых сторон и параллельности оснований новой фигуры?
Подсказка 5
Вспомним, что средняя линия трапеции меньше её диагонали. Как это поможет доказать, что равенство возможно только в вырожденном случае?
Так как сумма любого -угольника равна
то сумма углов любого шестиугольника, не обязательно выпуклого, равна
Поэтому из условия
следует, что
что, в свою очередь, влечет равенство треугольников
и
по двум сторонам и углу между ними. Так как углы
и
равны, а
четырехугольник
— вписанный. Хорды
и
его описанной окружности равны, поэтому
является равнобокой
трапецией.
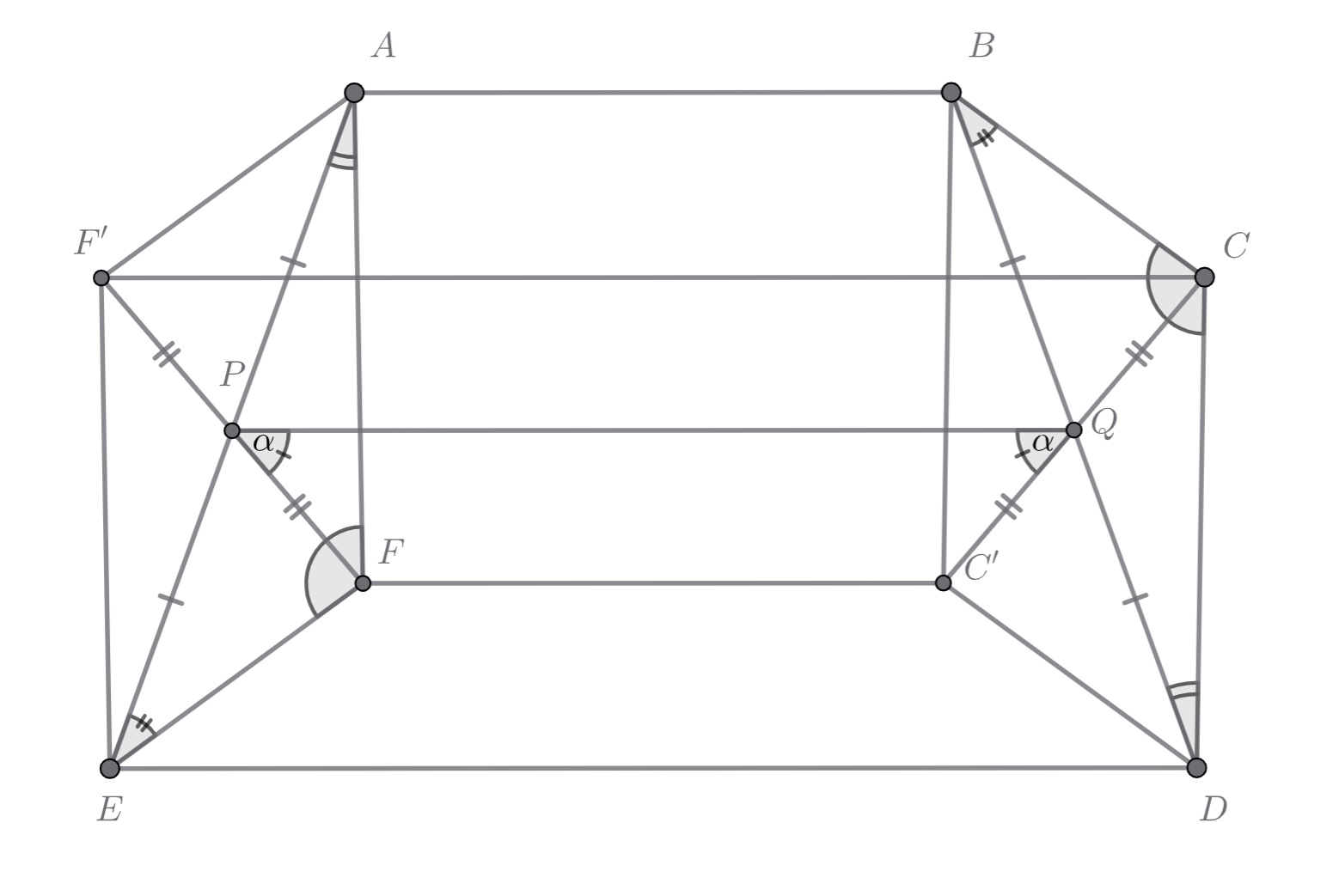
Пусть, без ограничения общности, Отразим точки
и
относительно середин
и
отрезков
и
соответственно, получим точки
и
Параллелограммы
и
равны, поэтому
Отсюда делаем вывод, что Расстояние от точки
до прямой
равно
что равно
расстоянию от точки
до прямой
На то же расстояние удалены точки
и
от прямой
поэтому четырехугольник
является равнобокой трапецией с основаниями
и
параллельными прямой
(и, соответственно,
и
).
Кроме того, отрезок
является общей средней линией для трапеций
и
и его длина равна
Но в
отрезок
является диагональю, которая всегда длиннее, чем средняя линия, если трапеция невырождена.
Равенство
возможно только если
и
обе попали на прямую
и
является вырожденной
трапецией.
Ошибка.
Попробуйте повторить позже
В комплекте для сборки игрушечного поезда есть один локомотив (который всегда расположен спереди), одинаковых красных вагонов и
одинаковых желтых вагонов. Назовем поезд длинным, если в нем есть хотя бы
вагонов (не считая локомотива). Сколько различных
длинных поездов можно собрать, используя этот комплект? (Ответ должен быть дан в замкнутом виде: в ответе не должно быть сумм с
переменным числом слагаемых, многоточий и т.д.)
Источники:
Подсказка 1
Сначала хотим найти количество всевозможных поездов, которые можем собрать. Так как длины поездов могут быть различны, удобно рассматривать каждую отдельно. Также, так как количество красных и жёлтых вагонов различно, хотим не рассматривать отдельные случаи (для больших длин, например, когда есть верхняя граница для красных вагонов). В этом случае удобно для каждой длины зафиксировать количество вагонов какого-то одного цвета, а потом выбрать другой цвет. Как это можно обобщить на сумму всех случаев?
Подсказка 2
В общем виде, для длины x, и, допустим, количества красных вагонов y, получаем, что количество поездов будет равно C из x по y (так как вагоны считаются одинаковыми, и нас интересует только расположение цветов). Теперь зафиксируем количество красных вагонов и просуммируем по всевозможным длинам поезда. Получаем какую-то неприятную сумму "цешек", которую, однако, можно упростить, если применить тождество Паскаля. Как нам это помогло?
Подсказка 3
Получаем телескопичесекю сумму, где остается только один биномиальный коэффициент. А теперь вспомним, что нам необходимо просуммировать эти результаты для всевозможного количества красных вагонов. Снова сводим к телескопической сумме. Что дальше?
Подсказка 4
Теперь остается только посчитать количество поездов, в которых менее n вагонов, чтобы вычесть его из общего количества поездов. Здесь задача проще: каждого цвета по количеству вагонов хватает для того, чтобы заполнить поезд любой длины, так что можно не так утруждаться. Как легко посчитать?
Подсказка 5
Можем просто считать, что для каждой позиции имеем 2 варианта: красный или жёлтый. Суммируем по всевозможным длинам (от 0 до n не включительно), вычитаем из ранее найденного и получаем ответ.
Посчитаем количество всех поездов, которые можно собрать в данном наборе, и потом вычтем количество поездов, в которых не более
вагонов.
Зафиксируем число
и посчитаем, сколько всего поездов с ровно
красными вагонами. Жёлтых вагонов может быть от
до
и для каждого числа
жёлтых вагонов от
до
мы выбираем
мест в строке длины
Таким образом, искомое
количество поездов с
красными вагонами равно сумме
Докажем, что эта сумма равна
Распишем каждое слагаемое, пользуясь следующим тождеством Паскаля:
Мы получим:
В каждой скобке вычитаемое равно уменьшаемому из предыдущей скобки. Нетронутым останется лишь уменьшаемое в последней скобке,
равное — это и есть искомый результат сложения.
Заметим, что в силу симметрии биномиальных коэффициентов этот результат можно переписать как
Теперь нужно сложить эти числа по всем от
до
Получим сумму
которая суммируется аналогичным образом через тождество Паскаля, и результат этого суммирования равен
Мы посчитали количество всех поездов. Осталось лишь вычесть количество поездов, в которых не более вагонов, но для каждого
количество поездов длины
очевидно равно
а всего в сумме таких поездов
Таким образом, длинных поездов
Ошибка.
Попробуйте повторить позже
Саша и Гоша поставили фишек в клетки доски
и по очереди ходят. Саша своим ходом может взять две фишки, стоящие
в левом верхнем и правом нижнем углу некоторого клетчатого прямоугольника (со сторонами больше
и поместить их по одной в две
другие угловые клетки того же прямоугольника. Гоша своим ходом может передвинуть любую фишку либо вправо вниз, либо влево вверх
по диагонали на любое число клеток. Они заканчивают ходить, когда кто-то не может сделать ход. Могут ли они ходить
бесконечно?
Источники:
Подсказка 1
Очень часто в задачах с процессом и вопросами "возможно ли? могут ли?" помогает идея зацепиться за величину, которая либо не меняется, либо меняется, но очень незначительно. Давайте внимательно посмотрим на их ходы и посмотрим, относительно каких клеток некоторых параметр не изменяется или увеличивается.
Подсказка 2
Рассмотрите диагонали, параллельные побочной.
Подсказка 3
Докажите, что общее количество фишек на каждой из указанных диагоналей либо не меняется, либо строго увеличивается.
Запишем в клетки доски положительные целые числа
так: число
записано в каждой клетке
й диагонали, параллельной главной диагонали, идущей слева сверху вправо вниз (ниже приведен пример для доски
Сопоставим каждой конфигурации фишек целочисленную величину которая равна сумме чисел в клетках, занятых фишками. Тогда
не меняется при действиях Гоши. Пусть последовательность
быстро растет как функция от
например,
Покажем, что в
этом случае
строго увеличивается с каждым действием Саши.
Пусть Саша выбрал прямоугольник, у которого левая верхняя и правая нижняя клетки имели числа и
Заметим, что в нашей
расстановке для всякого числа
числа, находящиеся строго ниже и левее него, имеют большие номера. Поэтому после хода Саши числа
изменятся с
и
на
и
, где
— высота выбранного прямоугольника, измеренная в клетках
Тогда
Значит, станет строго больше. При этом
все время остается целочисленным. Так как
ограничено сверху (как минимум, оно
меньше, чем
игра не может продолжаться бесконечно.
Не могут
Ошибка.
Попробуйте повторить позже
При каких существует такой набор из
прямоугольников, что из них можно собрать прямоугольник (без пустот и наложений), а
из любого меньшего их подмножества, состоящего из хотя бы двух прямоугольников, — нельзя?
Источники:
Подсказка 1
Попробуйте определить некоторое разбиение (в дальнейшем будем называть его спиральным) клетчатого прямоугольника [(n+1)/2]×[(n+1)/2].
Подсказка 2
Нарисуем спираль, начиная двигаться из угла вдоль короткой стороны прямоугольника, если они не равны. Затем расположим в центре спирали квадратик 1×1, за ним — прямоугольник 1×2, а затем будем накрывать все непокрытые клетки частично покрытого отрезка спирали прямоугольником ширины 1 и соответствующей длины. Что еще нужно сделать в этом разбиении?
Подсказка 3
Нужно построить спиральное разбиение клетчатого прямоугольника со столбцами и строками неравной ширины.
Подсказка 4
Определим ширину столбца i как wᵢ = (n+1)ⁱ⁻¹, а ширину строки j как hⱼ = C ⋅ (n+1)ʲ⁻¹, где С = (n+1)ⁿ⁺³. Теперь разбейте неравномерный клетчатый прямоугольник на меньшие. Какие прямоугольники можно из них сложить?
Подсказка 5
Посчитайте суммарную площадь малых прямоугольников.
Подсказка 6
Что, если в прямоугольнике, сложенном из малых прямоугольников, два прямоугольника ориентированы по-разному?
Подсказка 7
Можно получить противоречие с величиной его площади.
Подсказка 8
Должно получиться, что если некоторый прямоугольник сложен из малых, то все малые прямоугольники в нем ориентированы одинаково.
Подсказка 9
Оцените для любого i количества прямоугольников ширины не более wᵢ и высоты не более hᵢ.
Подсказка 10
Предположим, что мы сложили из подмножества малых прямоугольников некоторый прямоугольник. Заметим, что верхняя сторона этого прямоугольника состоит из сторон малых прямоугольников. Как тогда можно представить ее длину? А длину высоты?
Подсказка 11
Пусть некоторая горизонтальная прямая пересекает прямоугольник и не содержит сторон малых прямоугольников. Чему тогда равна суммарная ширина всех малых прямоугольников, которые пересекает эта прямая?
Подсказка 12
Вычислите, сколько четырёхугольников ширины wᵢ пересекает любая такая прямая.
Подсказка 13
Сколько тогда из них можно сложить прямоугольников, и какого они будут размера?
Подсказка 14
Получится, что мы можем собрать из подмножества малых прямоугольников прямоугольник побольше тогда и только тогда, когда они лежат на пересечении некоторых строк и столбцов исходного клетчатого прямоугольника.
Подсказка 15
Постройте спиральное разбиение для исходного прямоугольника. Предположим, что из некоторого подмножества A прямоугольников спирального разбиения, состоящего из хотя бы двух прямоугольников, можно собрать прямоугольник. Попробуйте рассмотреть прямоугольники разбиения.
Подсказка 16
Назовем прямоугольник, содержащий внешний конец спирали, ключевым, а прямоугольник, расположенный на внутреннем конце спирали, — центральным. Пусть ключевой прямоугольник оказался вертикальным (все его клетки лежат в одном столбце). Также предположим, что он не входит в А. Что можно сказать о следующем за ним прямоугольнике?
Подсказка 17
Докажите, что если ключевой прямоугольник не входит в А, то следующий за ним тоже не входит.
Подсказка 18
Предположим, что ключевой прямоугольник входит в А. Что, если центральный прямоугольник также будет входить в А?
Подсказка 19
Тогда в множество А входят все прямоугольники, содержащие клетку на пересечении строк, содержащих клетки ключевого прямоугольника, и столбца, в котором лежит центральный прямоугольник.
Подсказка 20
Пусть центральный прямоугольник не входит в А. Что можно сказать о прямоугольниках, содержащих клетку на пересечении строк, содержащих клетки ключевого прямоугольника, и столбца, в котором лежит центральный прямоугольник?
Для начала определим разбиение клетчатого прямоугольника
которое в дальнейшем будем называть спиральным. Нарисуем спираль, начиная двигаться из угла вдоль короткой стороны
прямоугольника, если они не равны. Затем расположим в центре спирали квадратик за ним — прямоугольник
а затем будем
накрывать все непокрытые клетки частично покрытого отрезка спирали прямоугольником ширины 1 и соответствующей
длины.
Для того, чтобы получить искомое разбиение, построим спиральное разбиение клетчатого прямоугольника со столбцами и строками
неравной ширины. Положим ширину столбца равной
а ширину строки равной
где
Далее разобьем неравномерный клетчатый прямоугольник на
прямоугольников (назовем их ) по линиям сетки. Выясним, какие прямоугольники можно сложить из подмножества множества
малых прямоугольников.
Заметим, что суммарная площадь малых прямоугольников равна
Заметим также, что если в прямоугольнике, сложенном из малых прямоугольников, два прямоугольника ориентированы
по-разному, обе его стороны имеют длину не менее а значит, его площадь будет не меньше
что, как мы увидели выше,
невозможно.
Тогда, если некоторый прямоугольник сложен из малых, все малые прямоугольники в нем ориентированы одинаково.
_________________________________________________________________________________________________________________________________________________________________________________
Утверждение 1. Пусть даны некоторые целые неотрицательные числа, не превышающие
Тогда если
то для всех
Предположим, что для некоторых различных наборов и
оказалось, что
Пусть — наибольшее число, при котором
Не умаляя общности положим, что Тогда
_________________________________________________________________________________________________________________________________________________________________________________
Утверждение 2. Пусть даны некоторые целые неотрицательные числа, не превышающие
Тогда если
то для всех
Доказывается аналогично утверждению 1.
_________________________________________________________________________________________________________________________________________________________________________________
По построению для любого малых прямоугольников ширины
не больше
а малых прямоугольников высоты не более
Предположим, что мы сложили из подмножества малых прямоугольников некоторый прямоугольник. Заметим, что верхняя сторона этого прямоугольника состоит из сторон малых прямоугольников, а значит, ее длина представима в виде
где — целые неотрицательные числа, не превышающие
Аналогично, высота прямоугольника представима в виде
где — целые неотрицательные числа, не превышающие
Пусть некоторая горизонтальная прямая пересекает прямоугольник и не содержит сторон малых прямоугольников. Тогда суммарная ширина всех малых прямоугольников, которые пересекает эта прямая, равна
Из утверждения 1 следует, что любая такая прямая пересекает ровно прямоугольников ширины
Значит, из всех
прямоугольников ширины
можно сложить
прямоугольников размера
Из утверждения 2 следует, что для каждого такого прямоугольника нам нужно использовать малых прямоугольников
высоты
Получается, для построения нашего прямоугольника нам понадобится не менее
малых прямоугольников
размера
С другой стороны, все малые прямоугольники различны, а значит, все
и
равны либо 0, либо
1.
Получается, что мы можем собрать из подмножества малых прямоугольников прямоугольник побольше тогда и только тогда, когда они лежат на пересечении некоторых строк и столбцов исходного клетчатого прямоугольника.
Построим спиральное разбиение для исходного прямоугольника. Предположим, что из некоторого подмножества прямоугольников
спирального разбиения, состоящего из хотя бы двух прямоугольников, можно собрать прямоугольник.
Назовем прямоугольник, содержащий внешний конец спирали, ключевым, а прямоугольник, расположенный на внутреннем конце спирали, — центральным. Не умаляя общности, предположим, что ключевой прямоугольник оказался вертикальным, то есть, все его клетки лежат в одном столбце.
Предположим, что ключевой прямоугольник не входит в Тогда следующий за ним по спирали прямоугольник тоже не входит в
иначе он будет единственным прямоугольником в
так как он содержит малый прямоугольник из столбца, все остальные клетки
которого заняты ключевым прямоугольником. По этой же причине мы сможем поочередно исключить все остальные прямоугольники из
Теперь предположим, что ключевой прямоугольник входит в Если центральный прямоугольник входит в
в него входят и все
прямоугольники, содержащие клетку на пересечении строк, содержащих клетки ключевого прямоугольника, и столбца, в котором лежит
центральный прямоугольник. Тогда в
входят прямоугольники из всех столбцов прямоугольника и всех строк, кроме, быть может, одной
(не пересекающейся с ключевым прямоугольником). Нетрудно заметить, что тогда все прямоугольники должны входить в подмножество
Наконец, если центральный прямоугольник не входит в ни один прямоугольник, содержащий клетку на пересечении строк,
содержащих клетки ключевого прямоугольника, и столбца, в котором лежит центральный прямоугольник, не может содержаться в
Из
этого следует, что ни один прямоугольник, кроме ключевого, не может входить в
Получается, состоит из всех прямоугольников разбиения, что и требовалось.
При всех
Ошибка.
Попробуйте повторить позже
Даны многочлены и
оба степени
со старшими коэффициентами
У каждого из них ровно
различных целых корней.
Известно, что все корни многочлена
четны, а все корни многочлена
нечетны. Докажите, что у многочлена
не
может быть целых корней.
Источники:
Подсказка 1
Как можно преобразовать многочлены, зная их корни?
Подсказка 2
Например, x² + 3x + 2 = (x + 2)(x + 1).
Подсказка 3
Подставьте вместо x некоторое число k. Каким оно может быть?
Подсказка 4
Что, если k — чётно?
Подсказка 5
Воспользуйтесь тем, что корни P(x) — чётные, а корни Q(x) — нечётные. Может ли их сумма обращаться в 0?
Пусть чётные числа — корни многочлена
а нечётные числа
— корни многочлена
Тогда:
Подставим в целое число
Возможны два случая:
чётно и
нечётно. В первом случае
чётно как произведение чётных чисел, а
нечётно как произведение нечётных чисел, поэтому, нечётно.
Аналогично в случае нечётного тогда
нечётно как произведение нечётных чисел, а
чётно как произведение чётных чисел,
и
опять нечётно. Таким образом,
нечётно при любом целом
и поэтому не может быть равно нулю, т.к. ноль —
четное число. Значит,
не имеет целых корней.
Ошибка.
Попробуйте повторить позже
Дана двусторонняя линейка без делений. Этот инструмент позволяет делать две операции:
1) провести прямую через две данные точки;
2) провести прямую, параллельную данной, на расстоянии 1 от нее.
Постройте с ее помощью (и не используя никакие другие инструменты) правильный треугольник.
Источники:
Подсказка 1
Попробуйте получить равносторонний треугольник из иных фигур.
Подсказка 2
Мы можем строить параллельные прямые, какие фигуры они могут нам дать?
Подсказка 3
Рассмотрите пересечение двух пар параллельных прямых.
Подсказка 4
Они образуют параллелограмм, а чему будут равны его высоты, если между параллельными прямыми расстояние равно единице?
Подсказка 5
Как раз единице высоты и будут равны. А чем тогда является наш параллелограмм?
Подсказка 6
Это ромб! Рассмотрите его диагонали.
Подсказка 7
Они пересекаются под прямым углом. Как можно тогда использовать вершины ромба? Попробуйте структурировать плоскость.
Подсказка 8
Проводя прямые, параллельные данным, мы построим клетчатую сетку из квадратов со стороной 1.
Подсказка 9
Осталось лишь подобрать точки, которые могут быть вершинами правильного треугольника, и провести через них прямые.
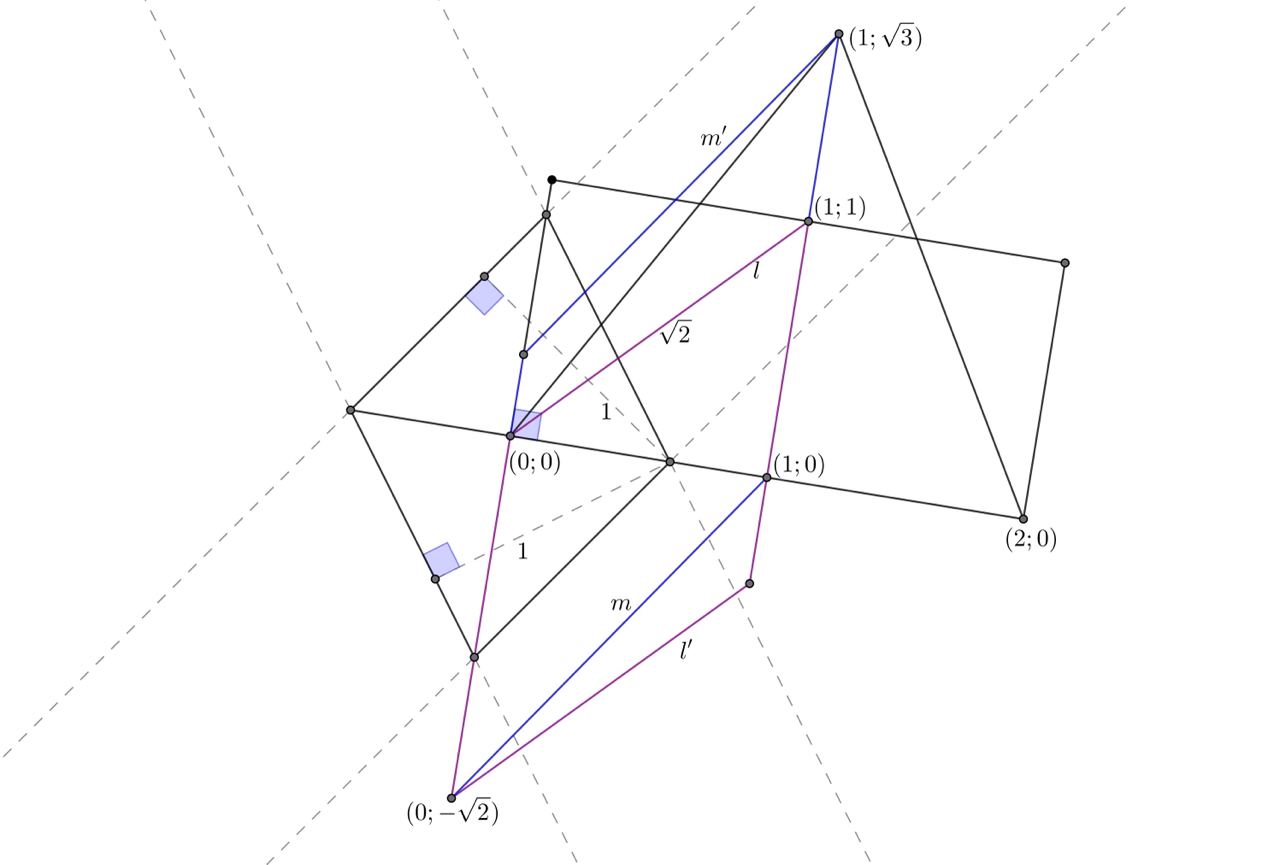
Для начала построим две пары параллельных прямых. На их пересечении образуется параллелограмм с одинаковыми высотами, равными
а значит, являющийся ромбом. Проведем его диагонали, как известно, являющиеся перпендикулярными. Заметим, что с помощью двух
этих перпендикулярных прямых и построения параллельных прямых на расстоянии
мы можем построить клетчатую сетку любого
конечного размера, состоящую из квадратиков со стороной
Введем систему координат с центром в одном из узлов сетки и с осями, параллельными сторонам клеток. Проведем прямую через
точки
и
Теперь проведем снизу от нее параллельную прямую
на расстоянии
Заметим, что на пересечении
пар прямых
и
образуется ромб со стороной длины
а значит,
проходит через точку
Теперь проведем прямую через пару точек
и
а также параллельную ей прямую
на расстоянии
сверху от нее.
На пересечении пар прямых
и
образуется ромб со стороной длины
а значит,
проходит через
точку
Осталось лишь соединить точки и
чтобы получить искомый равносторонний треугольник.
Ошибка.
Попробуйте повторить позже
На плоскости отмечено 8 точек, никакие три из которых не лежат на одной прямой. Между каждыми двумя проведен либо красный, либо синий отрезок. Красные отрезки не имеют общих точек, кроме, возможно, отмеченных точек. Обязательно ли найдется треугольник с вершинами в отмеченных точках, все стороны которого синие?
Источники:
Подсказка 1
Нам надо либо предъявить данный треугольник для любого возможного типа графа, либо придумать антипример. Что проще?
Подсказка 2
Конечно же, второй вариант. А как удобнее будет строить такой граф?
Подсказка 3
Попробуйте разделить точки на несколько уровней/групп. Хотелось бы как-то сократить перебор возможных вершин синего треугольника...
Подсказка 4
Пусть точки каждого уровня будут связаны между собой только красными отрезками, значит, если синий треугольник существует, то его вершины лежат на разных уровнях.
Пример
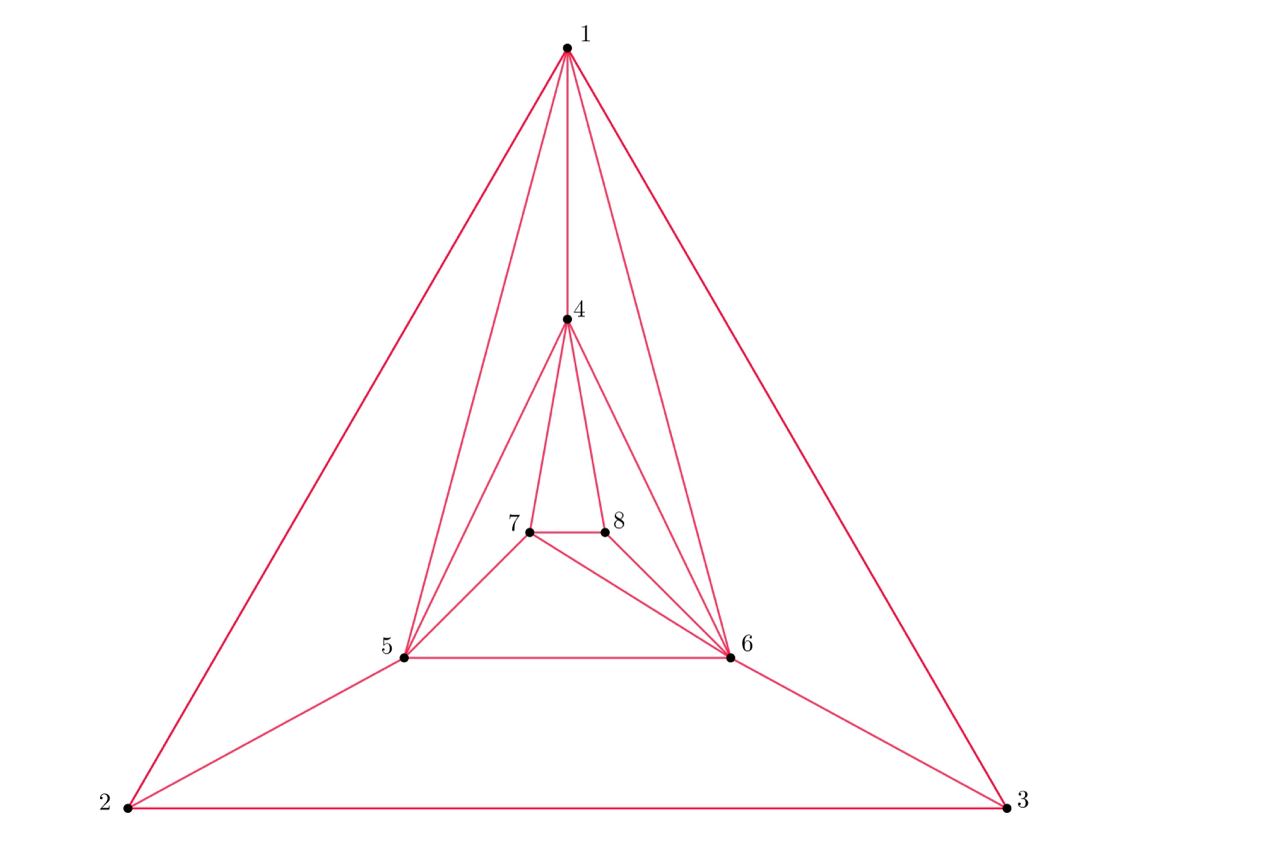
Рассмотрим набор точек, изображенных на иллюстрации. Для простоты восприятия проведем только красные отрезки.
Докажем, что синего треугольника не найдется. Для этого разделим точки на три уровня: точки
и
будут принадлежать
внешнему уровню, точки
и
— среднему, а
и
— внутреннему. Заметим, что на каждом уровне все точки соединены
между собой красными отрезками, а значит, если синий треугольник существует, все его вершины находятся на разных
уровнях.
Вершина соединена со всеми вершинами среднего уровня, а значит, не может быть вершиной синего треугольника. Аналогично,
вершина
соединена со всеми вершинами внешнего уровня, а значит, не может быть вершиной синего треугольника. Тогда вершина
соединена со всеми вершинами среднего уровня, кроме
и не может быть вершиной синего треугольника. Значит, ни одна
вершина внутреннего уровня не является вершиной треугольника с синими сторонами, а значит, такого треугольника не
найдется.
_________________________________________________________________________________________________________________________________________________________________________________
Пример
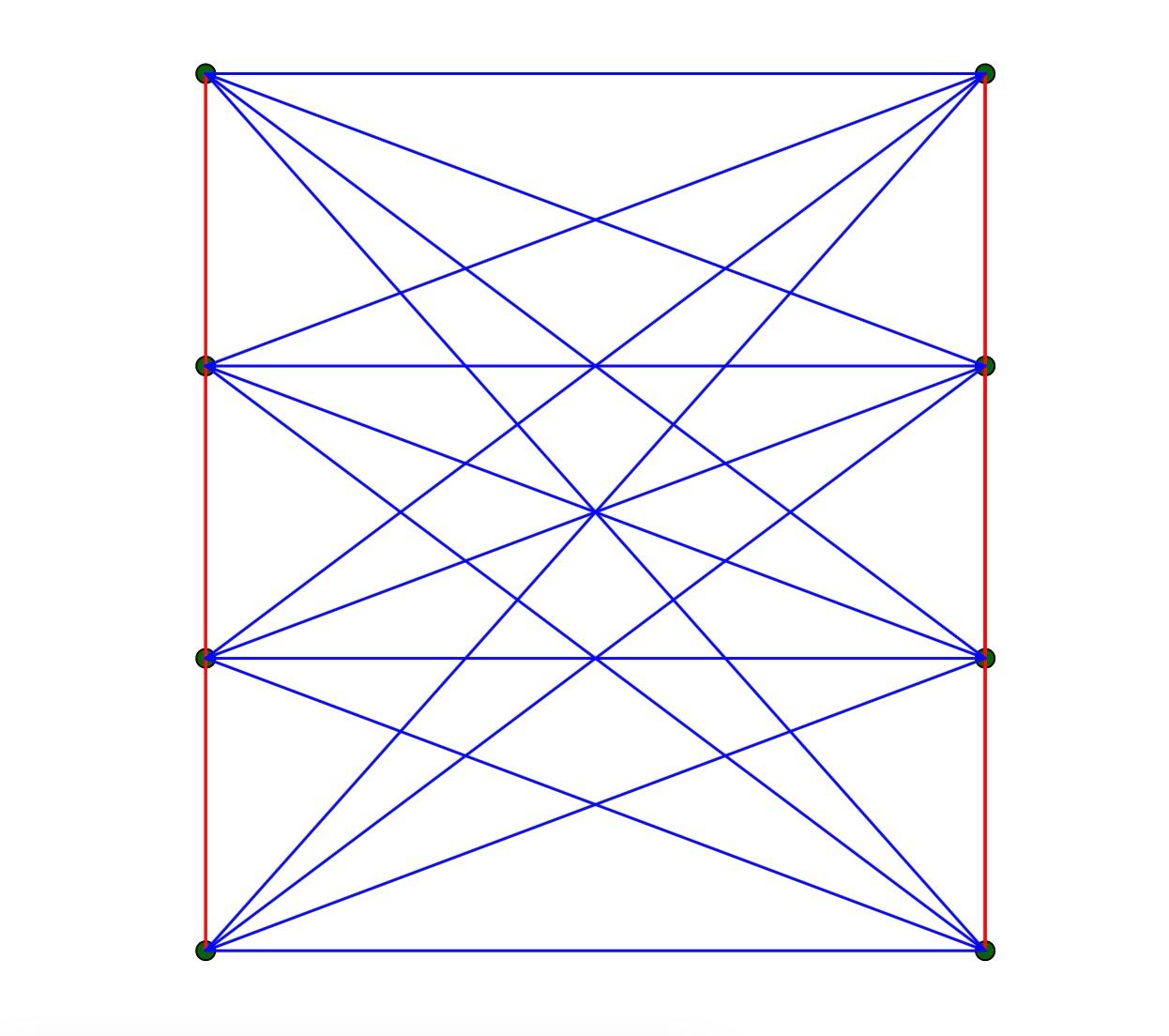
Возьмем два графа с красными ребрами. Тогда синие отрезки образуют граф
то есть двудольный граф, в
котором могут быть только циклы четной длины, а треугольник — это цикл нечётной длины, следовательно треугольников
нет.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Если точек или более, то синий треугольник обязательно найдется. Другими словами, граф, дополнительный к
планарному на
и более вершинах, всегда содержит граф-треугольник в качестве подграфа.
Не обязательно
Ошибка.
Попробуйте повторить позже
Разрежьте фигуру, составленную из одинаковых равносторонних треугольников (см. рисунок), на три (не обязательно равные) части и сложите из них равносторонний треугольник.
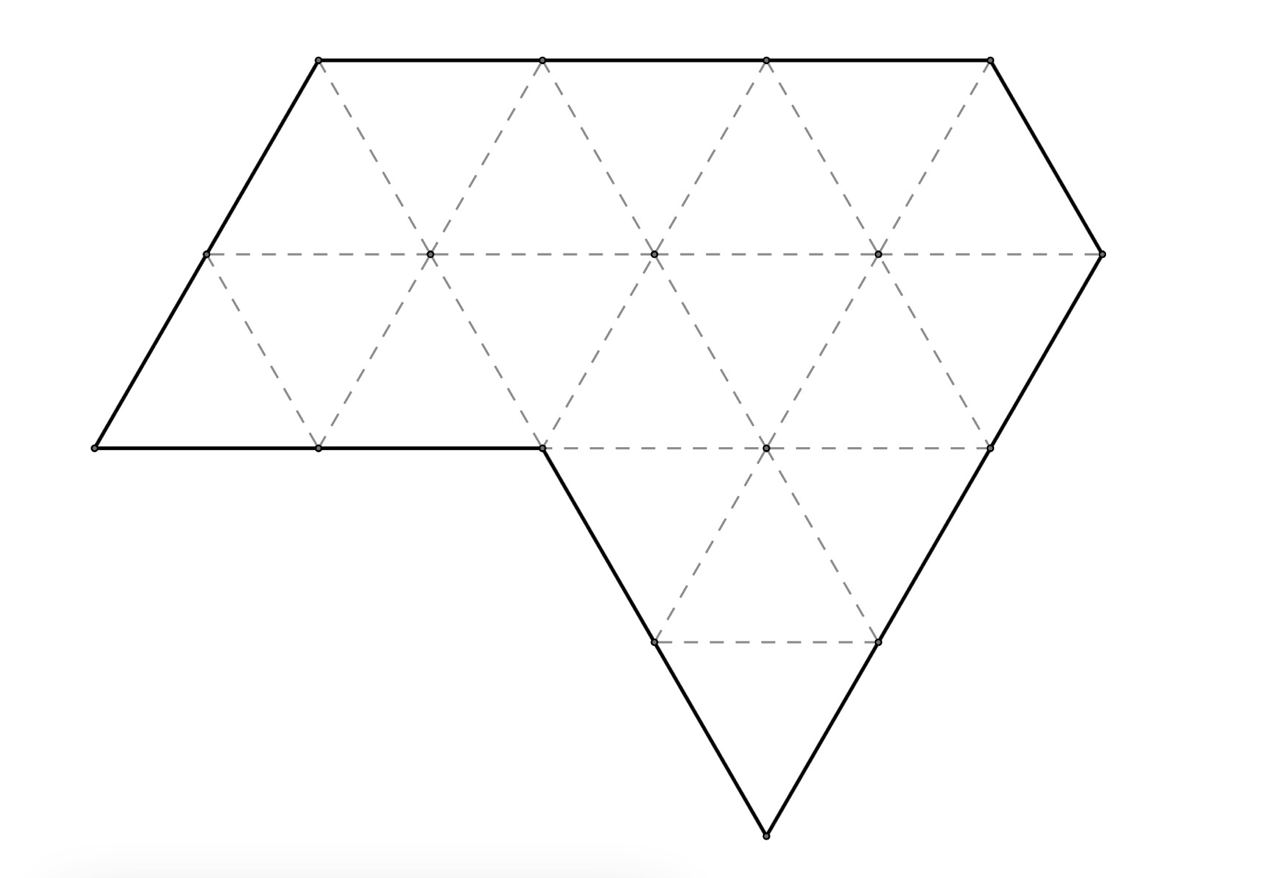
Источники:
Подсказка 1
В задаче два этапа — поиск разбиения и доказательство того, что оно подходит. Начнем с первого. Как стоит подойти к поиску частей для нашего треугольника?
Подсказка 2
А что, если "прикладывать" к картинке треугольник?
Подсказка 3
Его стороны и будут линиями разреза. Фигуры, которые окажутся внутри треугольника, мы не будем перемещать, а теми, что остались снаружи, надо будет заполнить пустые области.
Подсказка 4
Попробуйте сделать так, чтобы фигуры снаружи треугольника были равны некоторым пустым областям внутри треугольника.
Подсказка 5
Например, можно разрезать фигуру по прямым CB и BK.
Подсказка 6
Рассмотрите точку пересечения прямых FD и BK.
Подсказка 7
Докажите, что на прямой, содержащей эту точку и точку G, будет лежать одна из сторон треугольника.
Подсказка 8
Перейдите к счёту углов.
Решение представлено на рисунке.
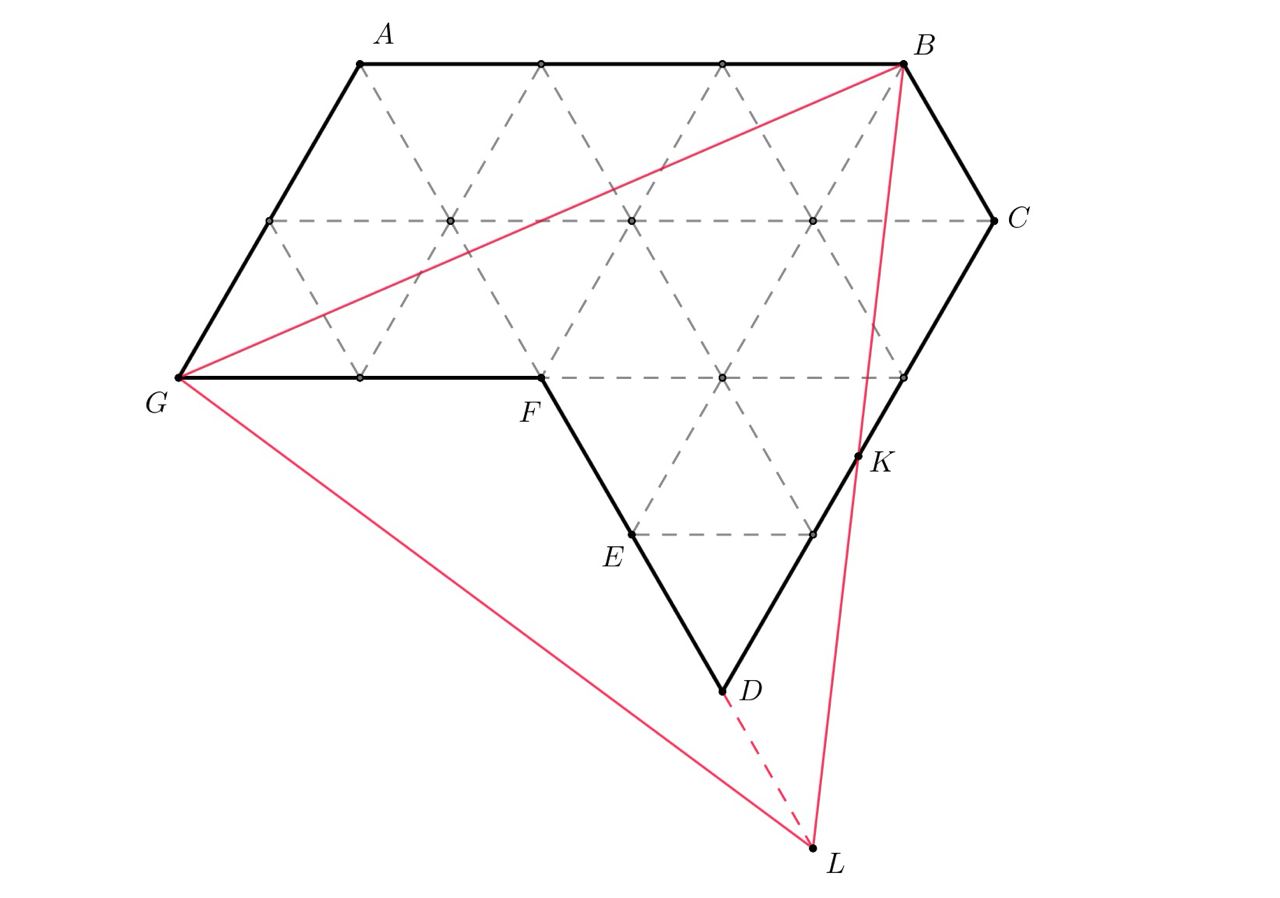
Покажем, что это действительно требуемое разрезание. Изначально был семиугольник Точка
получена отражением
точки
относительно точки
— середины стороны
в результате чего получен треугольник
равный треугольнику
При этом,
откуда следует, что треугольники
и
равны по двум сторонам (
и
) и углу
между ними
Таким образом, треугольники и
совместятся после разрезания и указанного перекладывания. Получится равносторонний
треугольник
длины сторон которого равны длине большей диагонали параллелограмма со сторонами
и
и тупым углом
Ошибка.
Попробуйте повторить позже
По кругу стоит несколько коробок. В одной из них 2025 камней, а остальные пусты. Разрешается взять два камня (возможно, из разных коробок) и переложить один в соседнюю коробку по часовой стрелке, а другой — в соседнюю против часовой стрелки. Через некоторое время все камни оказались в одной и той же коробке, соседней с начальной. Докажите, что один из камней побывал во всех коробках.
Источники:
Подсказка 1
Занумеруем коробки от 0 до n-1. Скажем, что сначала камни были в нулевой коробке, а в конце — в первой.
Подсказка 2
А как именно мы будем вычислять номер коробки, в которой будет находиться камень, при перекладывании?
Подсказка 3
Если мы переложим камень по часовой стрелке из коробки k, то он окажется в коробке (k + 1) mod n. А давайте избавимся от взятия остатков.
Подсказка 4
Можно задать это отдельно: скажем, что у нас есть бесконечное количество кувшинов, в самом начале в кувшине с номером 0 будет 2025 шаров. При перекладывании камня i из коробки с номером k в коробку (k + 1) mod n, мы также переложим шар с номером i из кувшина k' в кувшин k' + 1.
Подсказка 5
В каких кувшинах окажутся шары в конце?
Подсказка 6
Их номера будут сравнимы с 1 по модулю n. А что можно сказать про сумму их номеров?
Подсказка 7
А как мы перекладываем камни?
Подсказка 8
Сумма номеров кувшинов всегда будет равно 0, при том за каждое перекладывание одно из слагаемых увеличивается на 1, а другое — уменьшается на 1. В кувшинах с какими номерами могут находиться шары в конце?
Подсказка 9
В кувшине с номером 0 не может быть шаров. Пусть шар с номером i оказался в кувшине с отрицательным номером. Посмотрите на остатки.
Подсказка 10
Как может меняться номер кувшина для i-го шара за одно перекладывание?
Занумеруем камни от до
Занумеруем коробки от
до
по или против часовой стрелки так, чтобы все камни в начале были
в
-й коробке, а в конце оказались в
-й.
Расставим бесконечное количество кувшинов в ряд (у каждого кувшина будет номер целое число). Положим в кувшин с нулевым
номером шаров, занумерованных от
до
Каждый ход, когда камень с номером
перекладывают из коробки номер
в
коробку номер
будем перекладывать шар номер
из кувшина
где он находился на момент перекладывания камня, в
кувшин номер
Аналогично, когда камень с номером перекладывают из коробки номер
в коробку номер
будем
перекладывать шар номер
из кувшина
где он находился на момент перекладывания камня, в кувшин номер
Таким образом, одновременно с перекладыванием двух камней мы будем перекладывать два шара. Заметим, что остаток по
модулю
от номера кувшина, в котором находится
-й шар, будет всегда равен номеру коробки, в котором находится
-й
камень.
Обозначим номер кувшина, в котором находится -й шар в данный момент, за
Мы только что выяснили, что тогда номер
коробки, в котором находится
-й камень, равен
Теперь ясно, что в конце все шары оказались в кувшинах, номера которых
сравнимы с
по модулю
Заметим, что сумма
в любой момент времени равна нулю: в начале она равна нулю, так как все шары были в кувшине с номером и каждый ход одно из
слагаемых увеличивается на
а другое — уменьшается.
Поскольку ни один из шаров в конце не находится в кувшине номер один из шаров, допустим
-й, оказался в конце в кувшине с
отрицательным номером. Поскольку этот номер сравним с
по модулю
номер кувшина
-го шара в конце концов оказался меньше
либо равен
Итого, номер кувшина -го шара каждый ход менялся не более, чем на
и в конце стал меньше либо равен
Но это значит, что
остатки от деления на
номера кувшина
-го шара пробежали все возможные значения от
(в начале) до
То есть номер
коробки
-го камня пробежал все возможные значения от
до
что и требовалось.
Ошибка.
Попробуйте повторить позже
Существует ли функция определенная на всей числовой прямой, такая, что для любого
выполнено равенство
Источники:
Подсказка 1
Хм, функция от функции... При подстановке каких-то иксов мы не получим ничего интересного, ведь нам не сильно помогает знание, например, f(f(0))=-1. Тогда какие ещё интересные точки можно попробовать поискать?
Подсказка 2
Давайте найдём неподвижные точки функции g(x)=f(f(x)), то есть решим уравнение g(x)=x.
Подсказка 3
Используя знание о неподвижных точках g(x), найдём неподвижные точки g(g(x)).
Подсказка 4
Попробуем найти g(g(f(1))). Распишем каждую g(x) как f(f(x)), а потом обратно соберём f(f(...)) в g(..), но в другом порядке. Что интересного можно сказать про единицу?
Подсказка 5
Предыдущее выражение можно преобразовать в f(g(g(1))), а единица — одна из неподвижных точек g(g(x)), значит, это просто f(1). Как это использовать?
Подсказка 6
Ага, получается g(g(f(1)))=f(1), значит, f(1) — неподвижная точка g(g(x)). Но мы ранее их находили, следовательно, мы теперь точно знаем, какие значения может принимать f(1).
Подсказка 7
Давайте посмотрим, чему может быть равно f(1), и в каждом случае поищем противоречие.
Подсказка 8
Скорее всего, оно будет связано с переходом в преобразованиях g(x)=f(f(x)), ведь мы знаем f(1) по рассматриваемому случаю и умеем напрямую считать g(x), потому что она задана в явном виде.
Предположим, что такая функция существует. Положим
Заметим, что
Также заметим, что
Два корня этого уравнения мы уже знаем, так как
Отсюда
Значит,
Заметим, что
Отсюда
Проверим все случаи:
1)
2)
3)
В любом случае приходим к противоречию, а значит, искомой функции не существует.
Не существует
Ошибка.
Попробуйте повторить позже
Многие учащиеся математического кружка остаются в нём преподавать после выпуска. Будем говорить, что Ваня является последователем Саши, если Ваня учился у Саши или если Ваня учился у ученика Саши, ученика ученика Саши и так далее. Преподаватель кружка называется народным, если у него есть последователи, и не менее половины из них — победители международной олимпиады IMO. Известно, что всего в кружке училось 100 победителей IMO. Какое наибольшее количество народных преподавателей может быть в этом кружке, если у каждого человека не более одного учителя и никто не является собственным последователем?
Источники:
Подсказка 1
У нас есть люди, причём некоторые из них связаны каким-то отношением... Всё это очень похоже на граф! Рассмотрим ориентированный граф, где вершины — это ученики и преподаватели кружка, а ребра ведут от учителя к его ученику. Каким будет этот граф?
Подсказка 2
Верно, это будет набор непересекающихся деревьев! Рассмотрим какого-нибудь народного учителя, не являющегося последователем другого народного учителя. Если среди его последователей k победителей IMO, то сколько среди них может быть народных учителей?
Подсказка 3
Общее число последователей не может быть больше 2k+1, значит, учителей среди них не больше 2k. Получается, в одном таком поддереве количество народных учителей не более, чем удвоенное количество победителей IMO. А верна ли эта оценка для всего графа?
Рассмотрим ориентированный граф, где вершины ученики и преподаватели кружка, а ребра ведут от учителя к его ученику. По условию
этот граф — лес. Оценка. Выберем какого-нибудь народного учителя который не является последователем другого народного учителя.
Пусть у вершины
последователей победителей IMO. Тогда не победителей IMO, у
не более чем
так как
— народный. А,
значит, всего вершин в поддереве
не более
из которых только
учителей могут будут народными, так хотя бы один человек
никого не учил. Осталось заметить, что поддеревья соответствующие разным выбранным народным учителям, не пересекаются. Поэтому
число народных преподавателей кружка не больше чем удвоенное число победителей IMO. Получили оценку на
Пример. Возьмём
ориентированный путь из
вершины. Победители IMO — это
нижних учеников. Тогда все преподаватели, кроме самого нижнего в
этом пути — народные.
Ошибка.
Попробуйте повторить позже
Окружность описана около треугольника
Биссектриса
пересекает
в точке
Докажите, что длина проекции
отрезка
на прямую
больше длины отрезка
Источники:
Подсказка 1
Какую еще проекцию можно рассмотреть?
Подсказка 2
Пусть точки K и M — проекции S на AB и BC соответственно. Будем считать без потери общности AB > AC. Что можно сказать о точках K и M?
Подсказка 3
Например, точка M будет являться серединой BC.
Подсказка 4
Попробуйте заметить точки, лежащие на окружности.
Подсказка 5
Это точки K, M, B, S. Рассмотрите треугольник AKL. Как он связан с вопросом задачи?
Подсказка 6
Какой вывод можно будет сделать, если мы докажем, что ∠ALK — тупой?
Подсказка 7
Тогда AK > AL! Попробуйте оценить сумму ∠LAK + ∠AKL.
Подсказка 8
При получении неравенства Вам может пригодиться взаимное расположение точек L и M.
Длины проекции на и на
совпадают, поэтому без потери общности
Пусть точки
— проекции
на
и
соответственно. Заметим, что точка
— попала на отрезок
а
— середина
а, значит, лежит на
Так же, точки
лежат на одной окружности.
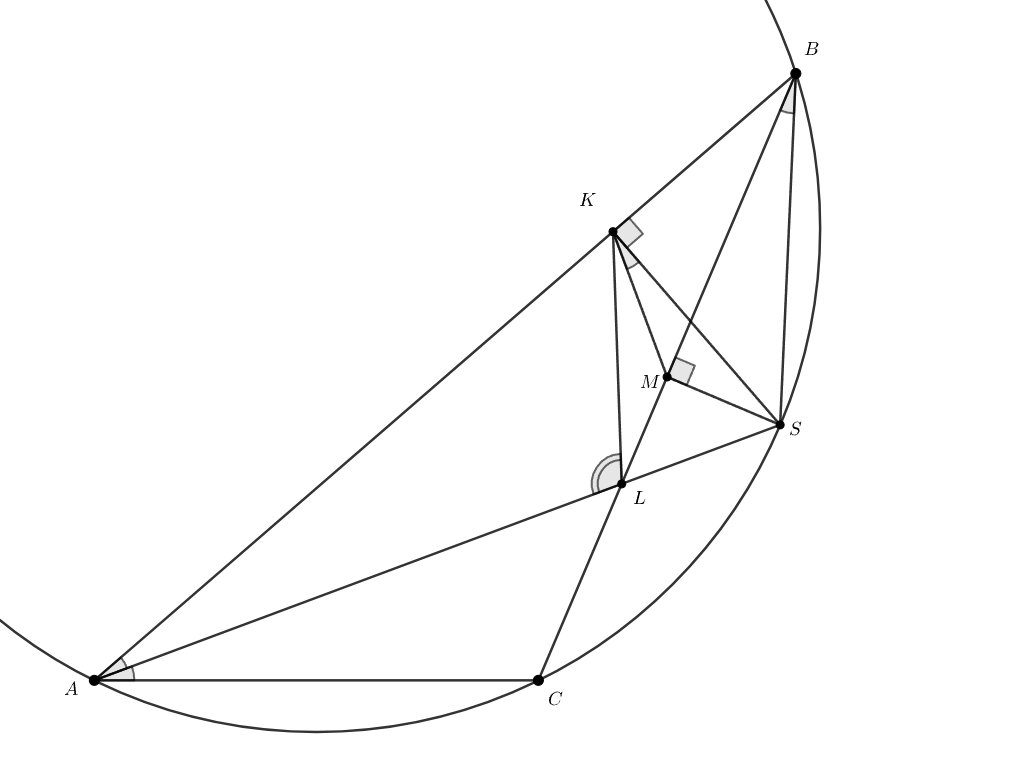
Докажем, что в угол
тупой, из этого сразу будет следовать, что
Для этого оценим
Пользуемся описанной окружностью треугольника и вписанностью
В последнем неравенстве воспользовались расположением точек и
Это неравенство даёт нам
а из этого
следует, что
— тупой.



