Высшая проба 2025
Ошибка.
Попробуйте повторить позже
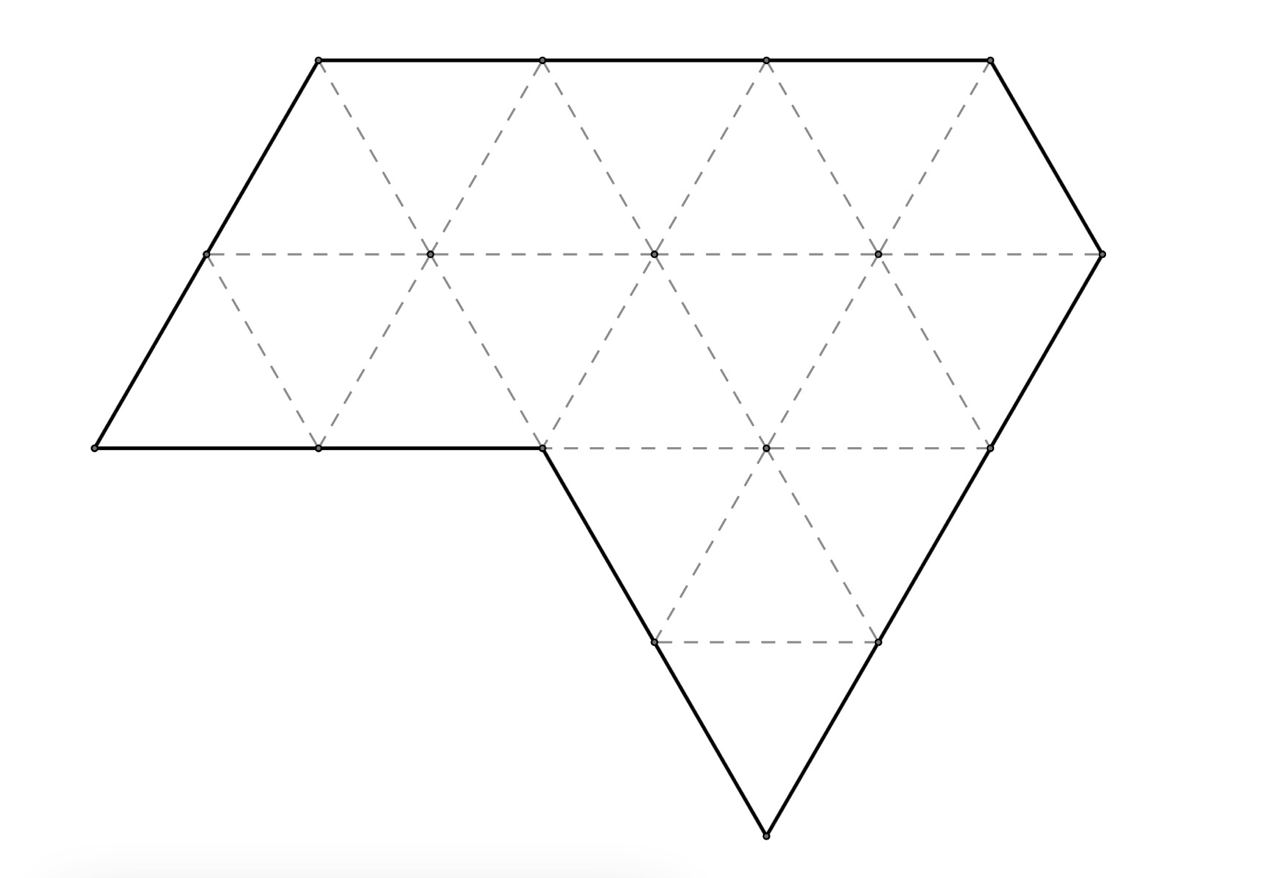
Разрежьте фигуру, составленную из одинаковых равносторонних треугольников (см. рисунок), на три (не обязательно равные) части и сложите из них равносторонний треугольник.
Источники:
Подсказка 1
В задаче два этапа — поиск разбиения и доказательство того, что оно подходит. Начнем с первого. Как стоит подойти к поиску частей для нашего треугольника?
Подсказка 2
А что, если "прикладывать" к картинке треугольник?
Подсказка 3
Его стороны и будут линиями разреза. Фигуры, которые окажутся внутри треугольника, мы не будем перемещать, а теми, что остались снаружи, надо будет заполнить пустые области.
Подсказка 4
Попробуйте сделать так, чтобы фигуры снаружи треугольника были равны некоторым пустым областям внутри треугольника.
Подсказка 5
Например, можно разрезать фигуру по прямым CB и BK.
Подсказка 6
Рассмотрите точку пересечения прямых FD и BK.
Подсказка 7
Докажите, что на прямой, содержащей эту точку и точку G, будет лежать одна из сторон треугольника.
Подсказка 8
Перейдите к счёту углов.
Решение представлено на рисунке.
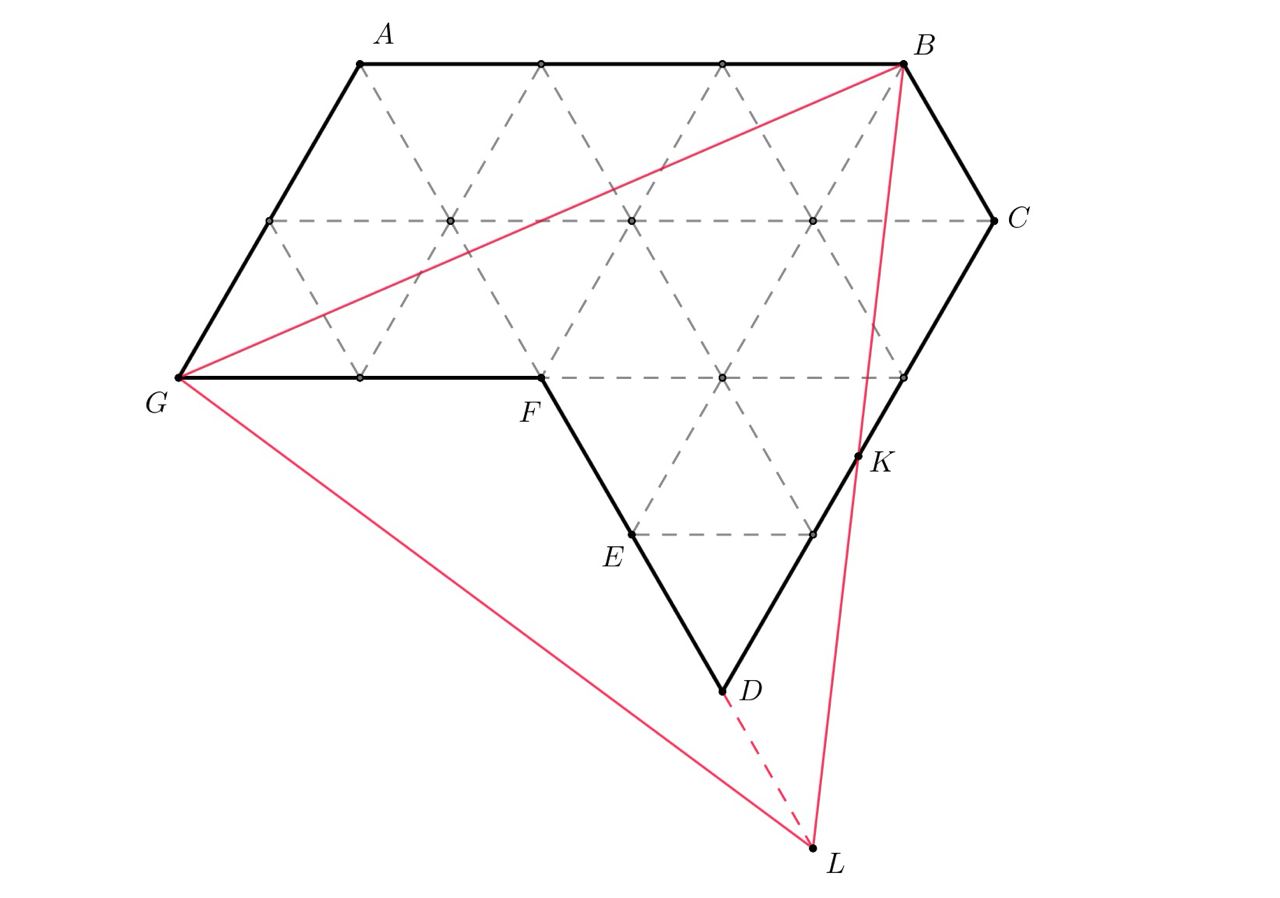
Покажем, что это действительно требуемое разрезание. Изначально был семиугольник Точка
получена отражением
точки
относительно точки
— середины стороны
в результате чего получен треугольник
равный треугольнику
При этом,
откуда следует, что треугольники
и
равны по двум сторонам (
и
) и углу
между ними
Таким образом, треугольники и
совместятся после разрезания и указанного перекладывания. Получится равносторонний
треугольник
длины сторон которого равны длине большей диагонали параллелограмма со сторонами
и
и тупым углом
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




