Регион 2025
Ошибка.
Попробуйте повторить позже
В треугольнике с углом
при вершине
медианы
и
пересекаются в точке
Прямая, проходящая через точку
и параллельная
пересекает описанную окружность треугольника
в точках
и
Найдите сумму углов
и
Источники:
Подсказка 1:
На рисунке имеется много параллельных прямых. Значит, можно попереносить отношения. Не забывайте, в каком отношении центр тяжести делит медианы.
Подсказка 2:
Первая подсказка намекала на то, что надо найти, как сотносятся отрезки AN, NR и RB — как 3 : 1 : 2. Теперь, используя это, попробуйте как-то поработать с окружностью.
Подсказка 3:
Поработать нужно даже не с окружностью, а со степенью точек относительно неё. Обратите внимание на точку пересечения PQ и AB (обозначим её через R).
Подсказка 4:
Пусть NR = x, RB = 2x, AN = 3x. Наверное, вы записали, что RP • RQ = RN • RA = 4x². Быть может, в выражении 4x² можно разглядеть что-то другое помимо RN • RA?
Подсказка 5:
На самом деле 4x² = BR². Это позволит некоторым образом удачно перекинуть углы и что-то понять про прямые BP и BQ в угле ABC.
Подсказка 6:
Итак, вы поняли, что BP и BQ — изогонали в угле ABC, аналогично можно сказать про прямые CQ и CR в угле ACB. Теперь осталось лишь выразить требуемую сумму углов через угол BAC.
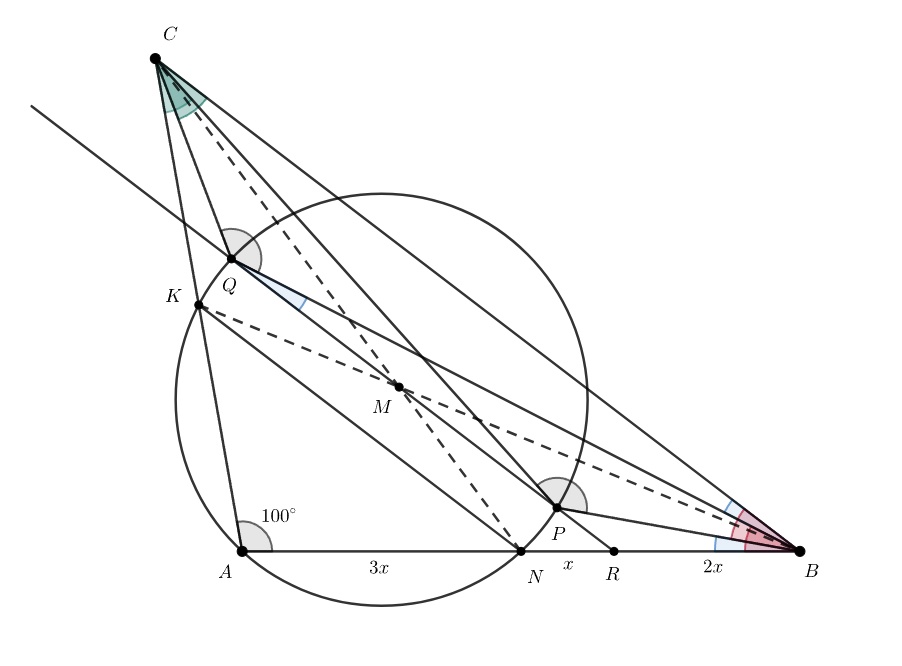
Обозначим через точку пересечения прямой
с отрезком
Заметим, что
— средняя линия треугольника
поэтому
Значит, по теореме Фалеса
последнее равенство следует из того, что — точка пересечения медиан треугольника
Обозначим Тогда
Поскольку четырёхугольник
вписанный,
имеем
Следовательно, прямая касается описанной окружности треугольника
поэтому
а тогда и
Рассуждая аналогично, получаем, что
Значит,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




