Регион 2025

Сначала приведём стратегию за Соню. Пока она не получила больше 299 монет, перед её ходом на доске остаётся хотя бы 101 монета. Разобьем доску на 100 квадратов Получается, что какие-то две монеты лежат в одном и том же квадрате Если эти две монеты соседние по стороне, то Соня надвигает одну на другую, и получает ещё одну монету. Если они стоят по диагонали, то Соня сдвигает одну из них в столбец к другой (здесь и далее столбец имеет длину 2, строка — длину 200). Теперь, какой бы ход ни сделала Даша, эти две монетки всё ещё будут соседними по стороне (либо одна будет снята и уйдёт в доход Сони), значит, своим следующим ходом Соня сможет получить ещё одну монетку. Таким образом, Соня всегда сможет увеличивать свой выигрыш, пока он меньше 300.

Теперь покажем, как играть за Дашу, чтобы Соня не получила больше 300 монет. Пронумеруем столбцы числами от 1 до 200 по порядку, выберем в каждом нечётном столбце по одной монетке и мысленно покрасим их в красный цвет. Даше достаточно обеспечить, чтобы красные монетки всегда оставались на доске. Для этого, в свою очередь, достаточно, чтобы две красные монеты никогда не попадали в одну клетку, потому что когда в клетку попадают красная и не красная монеты, можно считать, что с доски снимается не красная.

Назовём расположение монет на доске стабильным, если по одной красной монете лежит в столбцах а ещё одна располагается в одном из двух последних столбцов 199, 200. Легко видеть, что после любого хода из стабильной позиции две красные монеты не окажутся в одной клетке. Даша будет играть так, чтобы после каждого её хода получалась стабильная позиция. Если после хода Сони позиция осталась стабильной, то Даша двигает сотую красную фишку между двумя последними столбцами, так же Даша поступит и своим первым ходом. Если же после хода Сони позиция перестала быть стабильной, то Соня подвинула одну из красных монет из некоторого столбца в соседний столбец. Тогда Даша своим ходом вернёт её в столбец Таким образом, на доске всегда останется хотя бы 100 монет, и Соня заработает не более трёхсот рублей.

Заметим, что

Пусть Заметим, что числа и взаимно просты. Предположим, что это не так, и оба этих числа делятся на простое число Тогда число

тоже делится на Тогда делится на а не кратно противоречие. Таким образом, произведение взаимно простых чисел и —– точный квадрат, тогда и каждое из них точный квадрат. Однако, число при даёт остаток 3 при делении на 4, поэтому оно точным квадратом быть не может. Остаётся разобрать случаи При получается решений нет. При мы получаем: что даёт единственное решение ,

Пусть , , , Тогда

Первое решение. Сложим первые два неравенства. Преобразуя, получаем неравенство:

Следовательно, Тогда аналогично для других двух переменных.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Не умаляя общности, предположим, что Тогда Добавив к обеим частям неравенства имеем:

откуда наибольшее из чисел Значит, и все числа меньше 1.

_________________________________________________________________________________________________________________________________________________________________________________

Третье решение. Из условия следует, что аналогично Также по неравенству о средних. Значит, аналогично и Не умаляя общности можно считать, что —– минимальное из чисел тогда откуда аналогично а тогда и

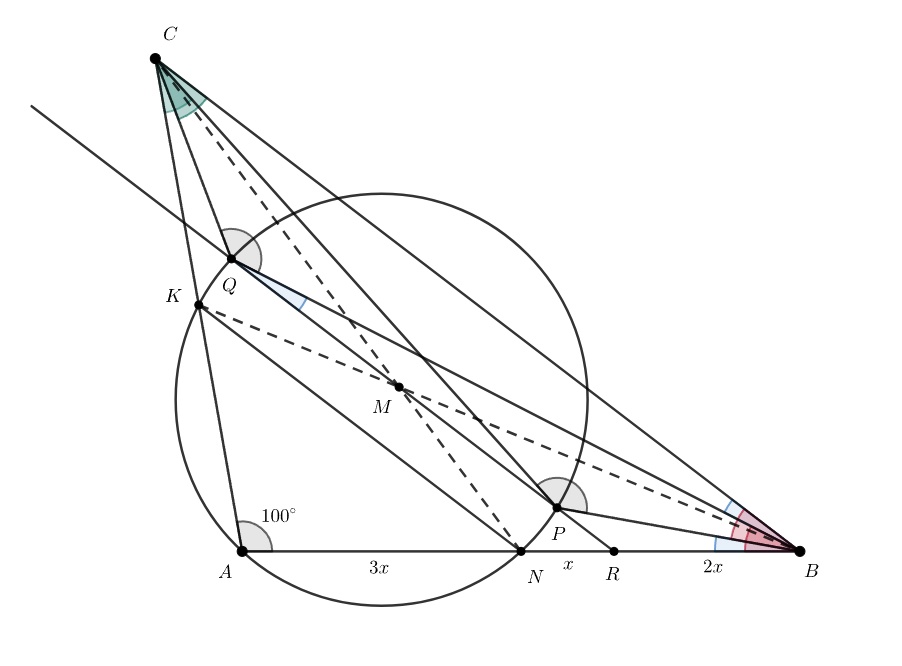
Обозначим через точку пересечения прямой с отрезком Заметим, что — средняя линия треугольника поэтому Значит, по теореме Фалеса

последнее равенство следует из того, что — точка пересечения медиан треугольника

Обозначим Тогда Поскольку четырёхугольник вписанный, имеем

Следовательно, прямая касается описанной окружности треугольника поэтому а тогда и Рассуждая аналогично, получаем, что Значит,

Полученная до разрезания конструкция состоит из 1024 отрезков нити, которые нить проходит поочерёдно слева направо и справа налево (пусть оба конца нити находятся слева). Тогда, если разрез проведён в см от левого края и в см от правого края, то длины полученных кусков нити равны и Поскольку этих длин всего две, то совпадает либо с либо с а наименьший кусок равен см. Значит, см или см, а общая длина нити, равная тогда может принимать значения см или см.

Первое решение. Назовём числа 0, 1, …, 49 маленькими, а остальные числа, которые могут появиться на табло, т.е. числа 50, 51, …, 99 — большими. Заметим, что после нажатия из маленького числа обязательно получается большое, а из большого числа — маленькое. Значит, после нечётного количества операций на табло будет гореть большое число.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Выстроим все целые числа от 0 до 99 в цепочку

Заметим, что если какое-то число горит на табло, то следующим числом может быть только соседнее число в цепочке. Но так как числа 0 и 25 стоят в цепочке на местах одной чётности, получить из числа 0 число 25 за нечётное количество шагов невозможно.

Обозначим общее число медведей через Тогда всего заплывов сделано не менее

С другой стороны, общее число заплывов равно количеству пар островов, то есть Таким образом,

откуда

и, следовательно,

Посчитаем, сколько медведей было в начале и в конце года на каждом из островов. В сумме получится не более потому что каждый медведь в начале и в конце года был на одном из островов. Поскольку

тогда по принципу Дирихле на каком-то острове в начале и в конце года в сумме было не более одного медведя.

Пусть в начале года на медведей не было, а в конце года там был ровно медведь. Тогда общее число заплывов, заканчивающихся на острове на больше общего числа заплывов, которые на острове начинаются. Таким образом, остров был начальной или конечной точкой для нечётного числа заплывов, но это количество должно равняться (по одному заплыву в каждую сторону для каждого из других островов), что чётно, – противоречие.

Аналогично выясняется, что наоборот тоже не бывает: если в начале года на острове был один медведь, а в конце года – ноль, то число заплывов, начинающихся на на больше числа заплывов, заканчивающихся на что снова даёт нечётное общее число заплывов, связанных с (но чётно).

Итого на острове и в начале, и в конце года медведей не было, что и требовалось.

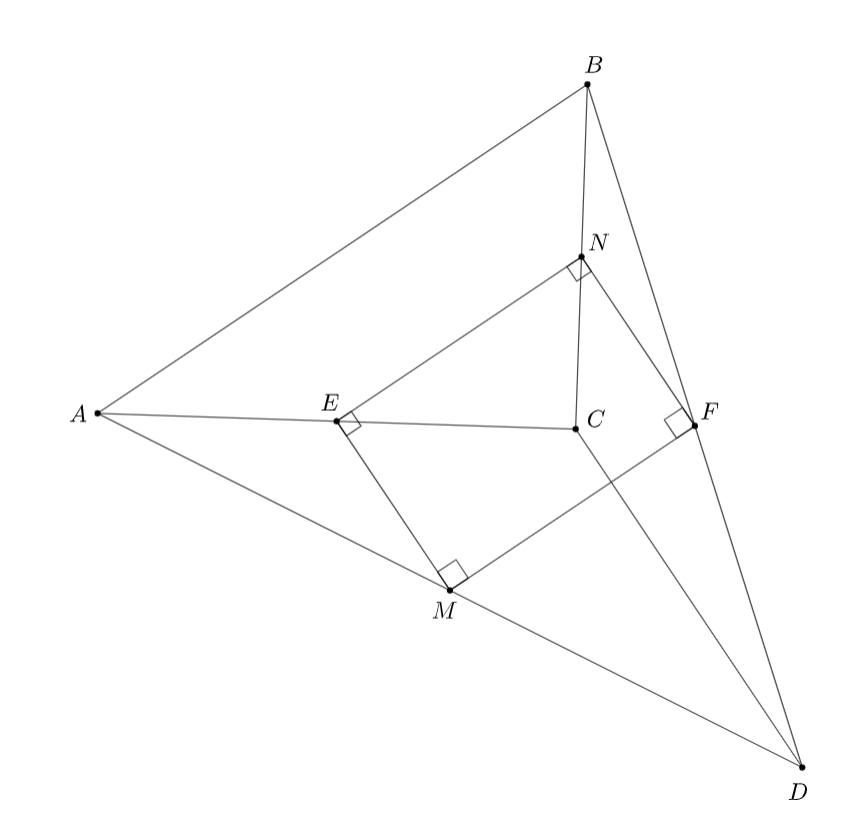
Обозначим через и середины отрезков и Тогда — средняя линия в треугольнике а — в треугольнике Следовательно, Аналогично Таким образом, точки лежат в одной плоскости, причём из условия следует, что — прямоугольник. Значит, равны его диагонали и

Заметим, что

по неравенству ломаной, остаётся вычесть из обеих частей.

Без ограничения общности можно считать, что многочленов с положительным старшим коэффициентом больше, чем с отрицательным (иначе домножим все многочлены на ). Тогда можно выбрать 100 многочленов …, с положительным старшим коэффициентом. Рассмотрим многочлены

где и Получается, что все многочлены тоже с положительными старшими коэффициентами. Значит, если они все не имеют корней, то

Но тогда

то есть многочлен

не имеет вещественных корней, противоречие.

Положим Покажем сначала, как выложить карточки так, чтобы больше 33 попарно не пересекающихся идеальных наборов не нашлось. Для удобства обозначим буквы в алфавитном порядке через через будем обозначать последовательность из карточек, на каждой из которых написана буква

Наш ряд будет состоять из 33 блоков выложенных друг за другом в этом порядке. Блок выглядит как:

(единственную карточку с буквой в этом блоке назовём особой). Ясно, что уже в -м блоке содержится идеальных наборов, у которых общей является только особая карточка. Докажем теперь, что в каждом идеальном наборе в полученном ряду есть особая карточка. Поскольку особых карточек всего 33, отсюда будет следовать, что из любых 34 идеальных наборов два обязательно пересекутся по какой-то особой карточке, то есть не может быть больше 33.

Действительно, предположим, что нашёлся идеальный набор, в котором нет особых карточек. Найдётся индекс такой, что буква этого набора встречается не правее блока (подходит хотя бы ); выберем наименьшее такое Если карточка нашего набора встречается левее то и также встречается в наборе левее то есть не правее это противоречит минимальности Значит, встречается именно в блоке то есть написана на особой карточке, что и требовалось.

Осталось показать, что попарно не пересекающихся идеальных наборов выбрать всегда можно. При обозначим через множество из идеальных наборов, не имеющих общих букв, кроме, возможно, (оно существует по условию). Мы выберем из каждого множества по набору так, чтобы в них не было общих карточек.

Для начала, если в каком-то множестве найдутся наборов, имеющих общую карточку (естественно, с буквой ), выделим такие наборов, выбросим из остальные наборы, а общую карточку назовём полезной для буквы Теперь мы будем по очереди выбирать набор из так, чтобы он не содержал полезных карточек для букв, отличных от и не пересекался с уже выбранными наборами.

Пусть наборы из уже выбраны. Если не существует полезной карточки с буквой то уже выбранные наборы содержат карточек с буквой каждая из которых встречается меньше раз в наборах в Выкинув эти наборы, будем считать, что карточки с в наборах из не содержатся в уже выбранных наборах (если полезная карточка с буквой есть, это уже выполнено), и в не меньше наборов.

Далее, выбранный набор содержит других карточек, каждая из которых содержится максимум в одном наборе из выкинув все эти наборы, оставим в как минимум наборов, не пересекающихся с уже выбранными. Среди этих наборов максимум содержат полезные карточки с буквами, отличными от выбрав любой набор, не содержащий такой карточки, мы завершим шаг.

После завершения 33-го шага мы получим 33 попарно не пересекающихся идеальных набора, что и требовалось.