Ломоносов 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
При каких значениях параметра 
уравнение
имеет на промежутке ![[−1;1]](/api/latex-service/v1/GetSession/268713/index-aa7433db96cbed6845c9fbea2457531f.svg)
единственное решение?
Источники:
Подсказка 1
А можно ли как-то преобразовать исходное равенство?
Подсказка 2
Попробуйте получить слева и справа одинаковые части.
Подсказка 3
Например, добавив и отняв справа а, можно получить 4ˣ - a.
Подсказка 4
В итоге имеем равенство вида |s| + |t| = s + t. Когда оно выполняется?
Подсказка 5
Раскрывая модули, можно получить неравенства для a и построить графики в координатах xOa. Не забудьте учесть, что нам нужно единственное решение на промежутке [-1;1]!
Наше уравнение может быть записано в виде
и, если к нему добавить условие попадания 
в промежуток ![[−1;1],](/api/latex-service/v1/GetSession/269206/index-4d690c14d5dbc127b6b9e9c3903dd47a.svg)
равносильно системе неравенств
Рассмотрим множество, которое задаётся этими неравенствами на плоскости с координатами 
и 
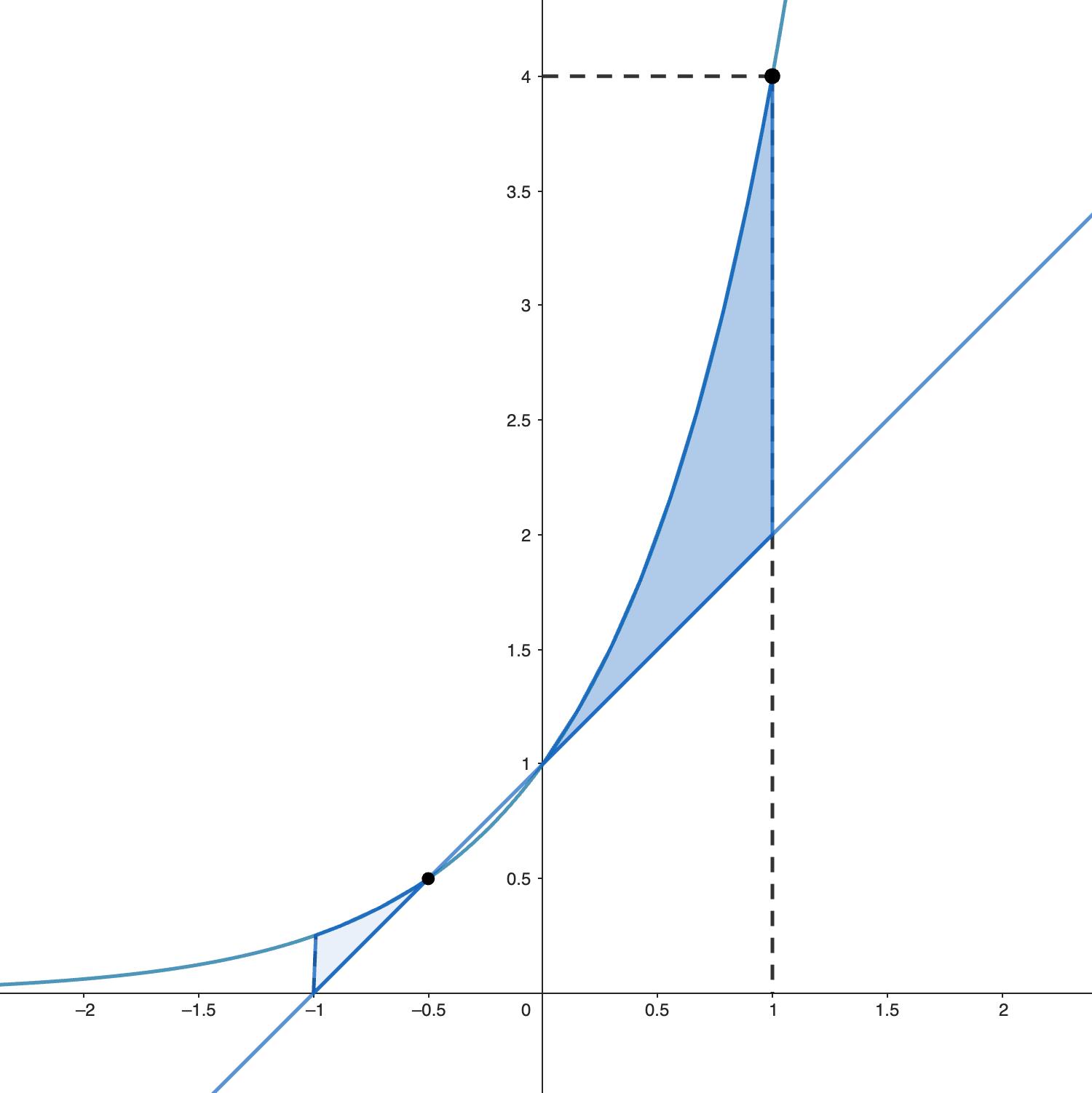
Графики функций 
и 
пересекаются в двух точках: 
и 
Функция 
выпукла вниз, поэтому при
![x ∈[−1;− 0.5]∪[0;1]](/api/latex-service/v1/GetSession/269206/index-1178ae9f89d3aa8c9f6646ca85bc619a.svg)
она больше функции 
а при ![x ∈[−0.5;0]](/api/latex-service/v1/GetSession/269206/index-fc3f1dec629fab14f59c6002fa927f4d.svg)
— меньше. Каждому 
соответствует одна горизонтальная
прямая на плоскости, и нас интересует, когда эта прямая пересекается с рассматриваемым множеством ровно в одной точке. Как видим, это
имеет место при следующих значениях параметра 
: 
(при этом 
); 
(при этом 
); 
(при этом 
); 
(при этом
).
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
