Тема Ломоносов - задания по годам

Ломоносов 2025

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ломоносов - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#125112Максимум баллов за задание: 7

Решите уравнение

∘ --2------- ∘-2------- ∘ -------2 ∘---√- ∘ --√-- 4x − 12x+ 9+ x − 6x+ 9+( −(x− 2)) = 3+ 8− 3− 8

Источники: Ломоносов - 2025, 11.1 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Для начала выпишем ограничения, а потом заметим, что под каждым корнем выделяются полные квадраты. Соответствующим образом преобразуем выражение.

Подсказка 2

Не забываем о том, что нужно навесить модули на подкоренные выражения после вынесения их из корня. Дальше выражение тривиально решается рассмотрением промежутков для подмодульных выражений.

Показать ответ и решение

Выделим полные квадраты при условии $x≤ 2:$

∘---2----------2- ∘ -2---------2- ∘-----√---- ∘ ---√----- (2x)− 2⋅2x⋅3+ 3 + x − 2⋅3⋅x+3 − x+ 2= 1 +2⋅ 2+2 − 1− 2 2+ 2

∘ ------- ∘ ------ ∘----√--- ∘ ---√---- (2x − 3)2+ (x− 3)2− x+ 2= (1+ 2)2 − (1 − 2)2

√- √ - |2x − 3|+|x− 3|− x+ 2= 1+ 2− ( 2− 1)

|2x− 3|+ |x− 3|= x.

То есть, с учётом ОДЗ, получаем, что $x∈[1.5;2].$

Ответ:

$[1.5;2]$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#125114Максимум баллов за задание: 7

Укажите наименьшее положительное значение $a,$ при котором неравенство

5− 1 x 2 x ≥ a+ sin2

не имеет ни одного решения $x >0.$

Источники: Ломоносов - 2025, 11.2 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Оставим только a в правой части и исследуем функцию в левой. Сначала рассмотрим каждое из слагаемых.

Подсказка 2

Нетрудно заметить, что первое слагаемое монотонно возрастает к 2^(5-(+0)), а sin(2^x) принимает любые значения из области значений и существует сколь угодно большой x, при котором -sin(2^x) = 1. Какой вывод можно сделать о максимальном значении функции?

Подсказка 3

Когда определили максимальное значение, легко найти минимальное а, которое больше этого значения и, соответственно, минимальное а, при котором неравенство не выполняется (обратим внимание на то, что слева максимальное значение первого слагаемого 2^(5-(+0)), а не 2⁵).

Показать ответ и решение

Рассмотрим функцию

5− 1 x f(x)= 2 x − sin2

Исследуем данную функцию. Имеем:

1.: $25− 1x$ — строго возрастающая к $25−0$ функция;
2.: $2x$ — неограниченно возрастающая функция, а, значит, найдутся сколько угодно большие $x,$ для которых выполняется равенство $sin 2x = −1.$

Тогда:

f(x)< 25+1 =33.

Значит, при $x> 0$ функция не принимает значений $a ≥33,$ а для любого $a< 33$ при некоторых достаточно больших $x> 0$ принимает значение, не меньшее $a.$

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 3#125176Максимум баллов за задание: 7

В окружность радиуса 3 вписан четырёхугольник, три стороны которого равны $3,3,3√2.$ Найдите максимально возможную площадь такого четырёхугольника.

Источники: Ломоносов - 2025, 11.3 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Сначала начертим сам четырёхугольник с окружностью, а потом соединим его вершины с центром окружности. Что мы можем сказать про получившиеся треугольники?

Подсказка 2

Нетрудно заметить, что два из них — равные правильные (со стороной 3), другой — прямоугольный с катетами 3 и гипотенузой 3√2. Их площади легко найти, так что разберёмся с оставшимся. Как можем найти его площадь (знаем как минимум две его стороны)?

Подсказка 3

Вспомним, что можно вычислить площадь прямоугольника через полупроизведение двух его сторон и синусу угла между ними. Так как все про остальные треугольники мы знаем, то и градусную меру этого центрального угла легко можем найти. Считаем оставшуюся площадь и складываем с площадями всех остальных треугольников, получая ответ.

Показать ответ и решение

Первое решение.

Решим задачу в общем случае. Обозначим четырехугольник $ABCD.$ Пусть $AB = BC = R,$ $√- CD = R 2.$ В такой конфигурации угол между сторонами $AB$ и $BC$ равен $∘ 120 .$ Угол $∘ ∠ADC = 60,$ как противолежащий.

$PIC$

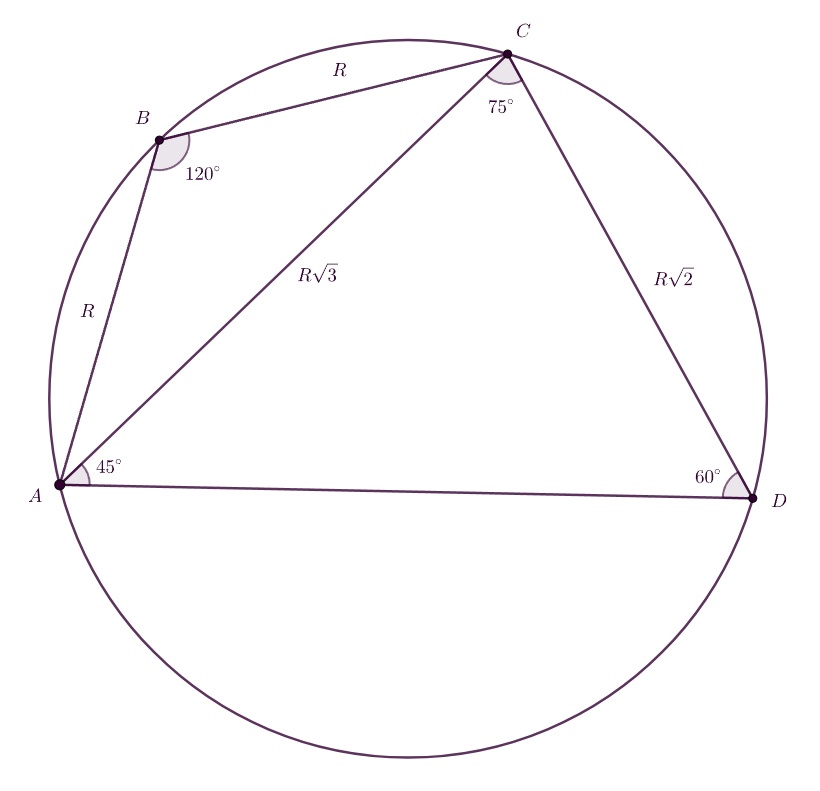
Диагональ $√- AC = R 3.$ Из теоремы синусов для треугольника $ACD$ следует, что угол $∠CAD$ равен $∘ 45$ (угол $∠CAD$ острый, т.к. иначе $∘ ∠CAD = 135,$ и сумма углов треугольника $ADC$ будет больше $∘ ∘ ∘ 60 +135 > 180$ ). Значит, угол $∠ACD$ равен $∘ 75.$ Площадь $S$ четырехугольника можно вычислить, как сумму площадей треугольников $ABC$ и $ADC.$

2√- SABC = R--3- 4

√- √ - √ - S = R2-6-⋅sin 75∘ = R2-6⋅cos15∘ = R2-3(1 +√3) ADC 2 2 4

R2√3 R2√3- √- 3R2 R2√3- S = -4--+ --4--(1+ 3)= -4- +--2--

Возможна другая конфигурация: $AB = CD =R,$ $√- BC =R 2.$ В этом случае четырехугольник — равнобочная трапеция с углом при основании $75∘.$

$PIC$

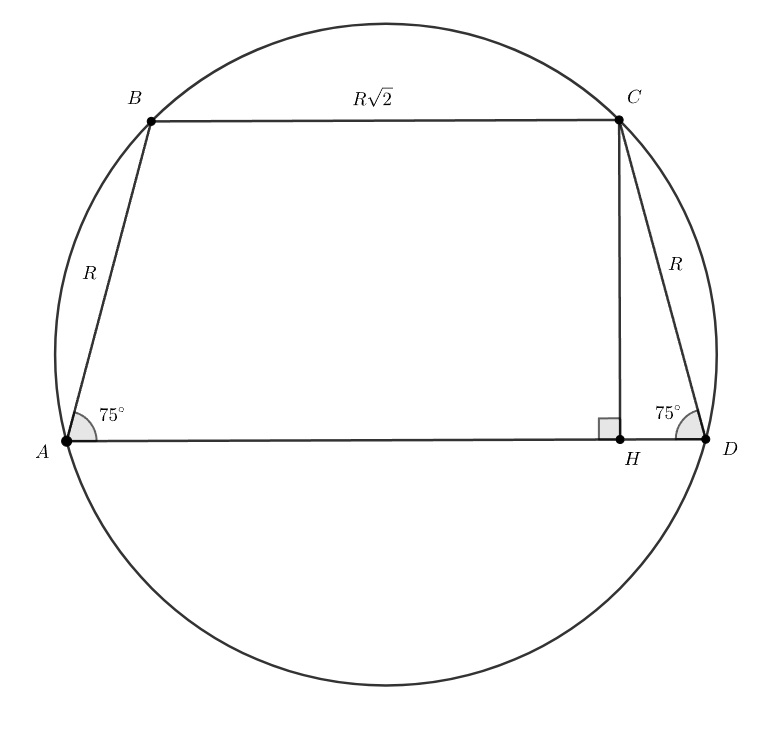
Тогда высота $CH = R sin75∘,$ и площадь трапеции равна

1 3R2 R2√3- S = 2(AD + BC)⋅CH = -4- +--2--

Оба варианта одинаковые, при подставновки $R= 3$ ответ равен

2 2√ - √- 3R-+ R---3= 27+ 9-3 4 2 4 2

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Соединим вершины четырехугольника с центром окружности.

$PIC$

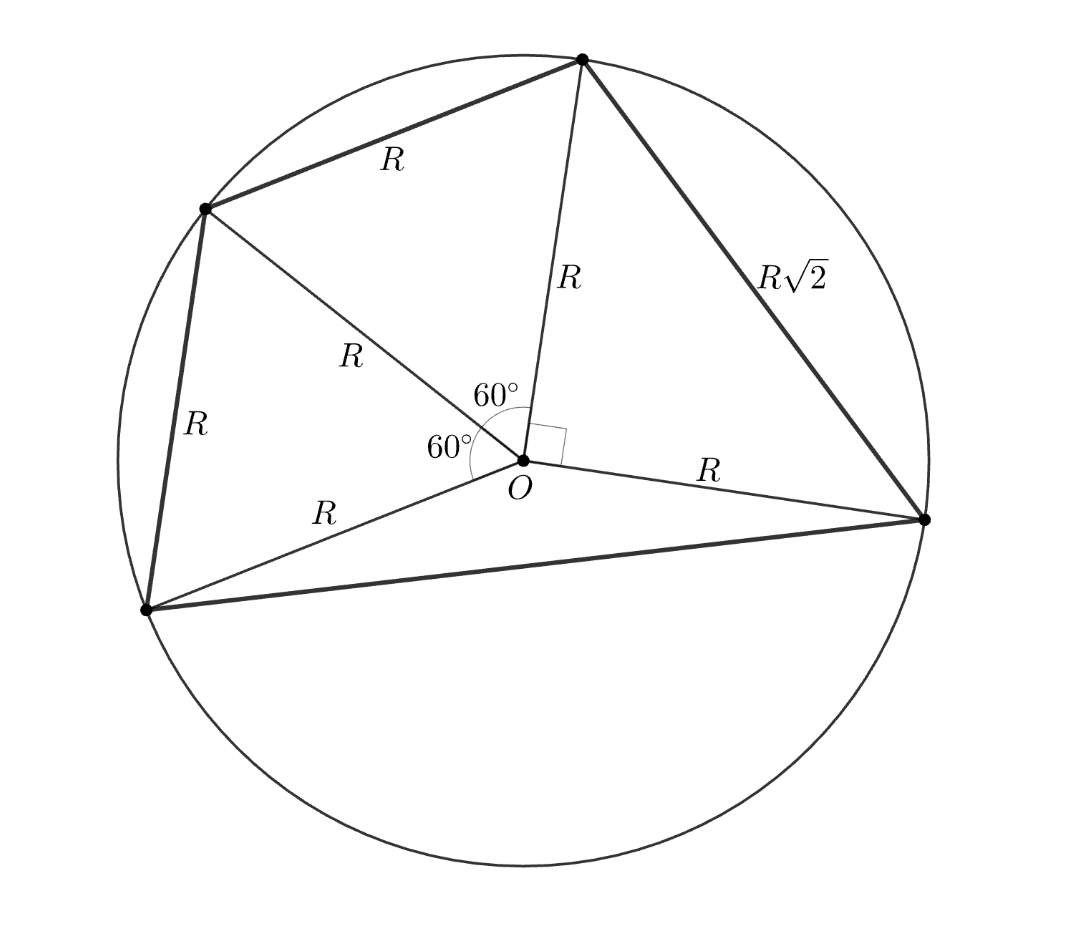
Получается, что четырехугольник составлен из двух правильных треугольников со стороной 3, площадь каждого $√ - 9--3 4 ;$ одного прямоугольного треугольника с катетами 3, 3 и гипотенузой $√- 3 2,$ площадь $92;$ одного равнобедренного треугольника со сторонами 3 и 3 и углом между ними $150∘,$ площадь равна

1⋅3⋅3⋅sin150∘ = 9 2 4

Суммарная площадь одинакова вне зависимости от того, в каком порядке они расположены, и равна

27 9√3 4-+ -2-

Ответ:

$27 9√3- 4 + 2$

Ошибка.
Попробуйте повторить позже

Задача 4#125177Максимум баллов за задание: 7

Найдите все решения уравнения

3 3 3 3 cos(πx)+ cos(2πx)− cos(4πx)=(cos(πx)+cos(2πx)− cos(4πx)),

принадлежащие отрезку $[0.3;1.6].$

Источники: Ломоносов - 2025, 11.4 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Хм, кажется будет полезно в этой задаче сделать замену. Давайте так и поступим! Заменим cos(πx) на a, cos(2πx) на b, -cos(4πx) на c. Теперь подумаем, когда такое равенство может выполняться.

Подсказка 2

Да, как бы ни было страшно, надо раскрыть скобки и привести подобные слагаемые. Затем полученное выражение легко разложится на множители! Действительно, уравнение имеет решение тогда и только тогда, когда какая-то из сумм(a + b, b + c, a + c) равна 0.

Подсказка 3

Не забудем формулу разности косинусов и решим каждое из получившихся уравнений, затем отберём корни, принадлежащие промежутку из условия.

Показать ответ и решение

Так как

3 3 3 3 2 2 2 2 2 2 (a +b+ c)− (a +b + c)= 3ab +3a c+3b a+3b c+3c a+ 3c b+ 6abc= 3(a+ b)(b+ c)(a+c),

то либо $cos(πx)+cos(2πx)= 0,$ либо $cos(2πx)− cos(4πx)= 0,$ либо $cos(πx)− cos(4πx)= 0.$

В первом случае

cos(2πx)=cos(π − πx)

⌊ 2πx =π − πx +2πk, k ∈ℤ ⌈ 2πx =πx − π +2πk, k ∈ℤ

⌊ 1 2k |⌈ x = 3 + 3-, k ∈ℤ x =− 1+ 2k, k∈ℤ

Во втором случае

cos(2πx)= cos(4πx)

⌊ ⌈ 4πx= 2πx+ 2πk, k∈ℤ 4πx= −2πx+ 2πk, k∈ ℤ

⌊ x= k, k∈ ℤ |⌈ k x= 3, k ∈ℤ

В третьем случае

cos(πx)= cos(4πx)

⌊ 4πx =πx +2πk, k ∈ℤ ⌈ 4πx =− πx+2πk, k ∈ℤ

⌊ 2k | x =-3 , k∈ ℤ |⌈ 2k x =-5 , k∈ ℤ

В указанный промежуток попадают корни

1 2 4 2 4 6 8 1,3,3, 3,5,5,5 ,5

Ответ:

$1, 1, 2, 4, 2, 4, 6, 8 3 3 3 5 5 5 5$

Ошибка.
Попробуйте повторить позже

Задача 5#125179Максимум баллов за задание: 7

Даны три функции

f(x)= (x +a )(x2+b x+ 6) , 1 1 ( 2 1 ) f2(x)= (x +a2)(x +b2x+ 8), f3(x)= (x +a3) x2+b3x+ 12

(здесь $a1,b1,a2,b2,a3,b3$ — положительные числа).

Для каждого действительного $x$ выполняется условие $f1(x)=f2(x) =f3(x).$ Найдите значение суммы $a1+ b1+a2+ b2+ a3 +b3.$

Источники: Ломоносов - 2025, 11.5 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Из того, что функции тождественные, можем получить определённые выводы. Посмотрим на первый множитель в каждой из функций. Какие корни в совокупности получаются из них?

Подсказка 2

Получаем, что у каждого из выражений корни -a₁, -a₂, -a₃. При этом, так как это максимально возможное число корней у многочленов третьей степени, то это единственные корни в каждом из выражений (причём они различны, подумайте, почему). Теперь хотим использовать теорему Виета со знанием этой информации в контексте вторых множителей.

Подсказка 3

Отсюда уже довольно просто находятся сначала а₁, а₂, а₃, а потом и b₁, b₂, b₃. Если столкнулись с проблемами на этапе применения теоремы Виета, то просто перемножьте все результаты, которые вы оттуда получили, и найдите сначала х₁ * х₂ * х₃.

Показать ответ и решение

Так как значения в каждой точке у функций совпадают, то $f =f = f . 1 2 3$ Тогда уравнение $f(x)= 0 1$ имеет отрицательные корни $x1 = −a1, x2 = −a2, x3 = −a3,$ и это три разных корня, так как если бы линейные множители в двух тождественно равных функциях были бы одинаковыми, то совпадали бы и квадратичные множители, а по условию задачи это не так.

Поэтому из теоремы Виета для каждого из квадратичных множителей следует:

x2 ⋅x3 =6, x1⋅x3 = 8, x1⋅x2 = 12

Перемножим три равенства, получим, что $(x x x)2 = (6⋅4)2, 1 2 3$ тогда из отрицательности корней следует, что $x xx = −24. 12 3$ Поэтому

−24 −24 −-24 x1 = 6 =−4, x2 = 8 = −3, x3 = 12 = −2.

Тогда $a1 =4, a2 = 3, a3 = 2,$ а по теореме Виета ищутся $b1 =3 +2= 5, b2 = 4+ 2= 6, b3 =4 +3= 7.$

Тогда ответ: $a1+ a2+ a3+b1+ b2 +b3 = 4+ 3+2 +5+ 6+ 7= 27.$

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 6#125181Максимум баллов за задание: 7

Газонная поливалка равномерно разбрызгивает вокруг себя воду в круге радиуса $4− 2√2.$ На границе этого круга расположена другая такая же поливалка. А ровно посередине между двумя поливалками находится вход в нору. Мышь, хозяйка норы, хочет вернуться домой, но не хочет сильно вымокнуть.

Найдите длину пути, на котором мышь намокнет меньше всего. Мышь может менять направление бега, но её скорость постоянна, и под душем двух поливалок мышь мокнет вдвое быстрее.

Источники: Ломоносов - 2025, 11.6 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте инвертируем путь мышки (т.е. представим, что мышка наоборот выбегает из норы). Очевидно, что ответ от этого никак не поменяется, а решать задачу будет проще. Хорошо, тогда часть своего пути мышь пробежит под двумя поливалками, а другую часть — только под одной.

Подсказка 2

Давайте попробуем чем-нибудь параметризировать траекторию, по которой бежит мышка. Ага! Мы можем задать траекторию бега мышки единственной точкой — точкой, в которой мышь выбегает из зоны двух поливалок. Назовём эту точку H. До (⋅) H мышке выгодней бежать по прямой, а дальше по радиусу одной из окружностей.

Подсказка 3

Пусть (⋅)A и (⋅)B — центры окружностей. Очевидно, что положение (⋅)H определяется углом ∠HAB, а также через этот угол и радиусы окружностей можно записать функцию, описывающую расстояние, которое пробежит мышка!

Подсказка 4

Запишем эту функцию, затем возьмём её производную и найдём локальный экстремум. Также не забываем, в каком диапазоне у нас может меняться ∠HAB! Проверим, что мы нашли именно минимум и найдём соответствующее ему расстояние.

Показать ответ и решение

Пусть радиус полива равен $R.$ В точках $A$ и $B$ расположены поливалки, нора находится в $O.$ Поменяем направление — пусть мышь выбегает из норы и стремится на сухую землю. Путь мыши может быть какой угодно формы, но, так или иначе, ей придётся покинуть область двойного полива — пусть это произойдёт в точке $H.$ Тогда оптимальный путь до точки $H$ — это отрезок $OH,$ а оптимальный путь от $H$ до сухой земли — это $HL,$ где $H$ лежит на радиусе $BL.$ Значит, кандидаты на оптимальный путь — ломаные вида $OHL$ и определяются они одним параметром — положением точки $H.$

$PIC$

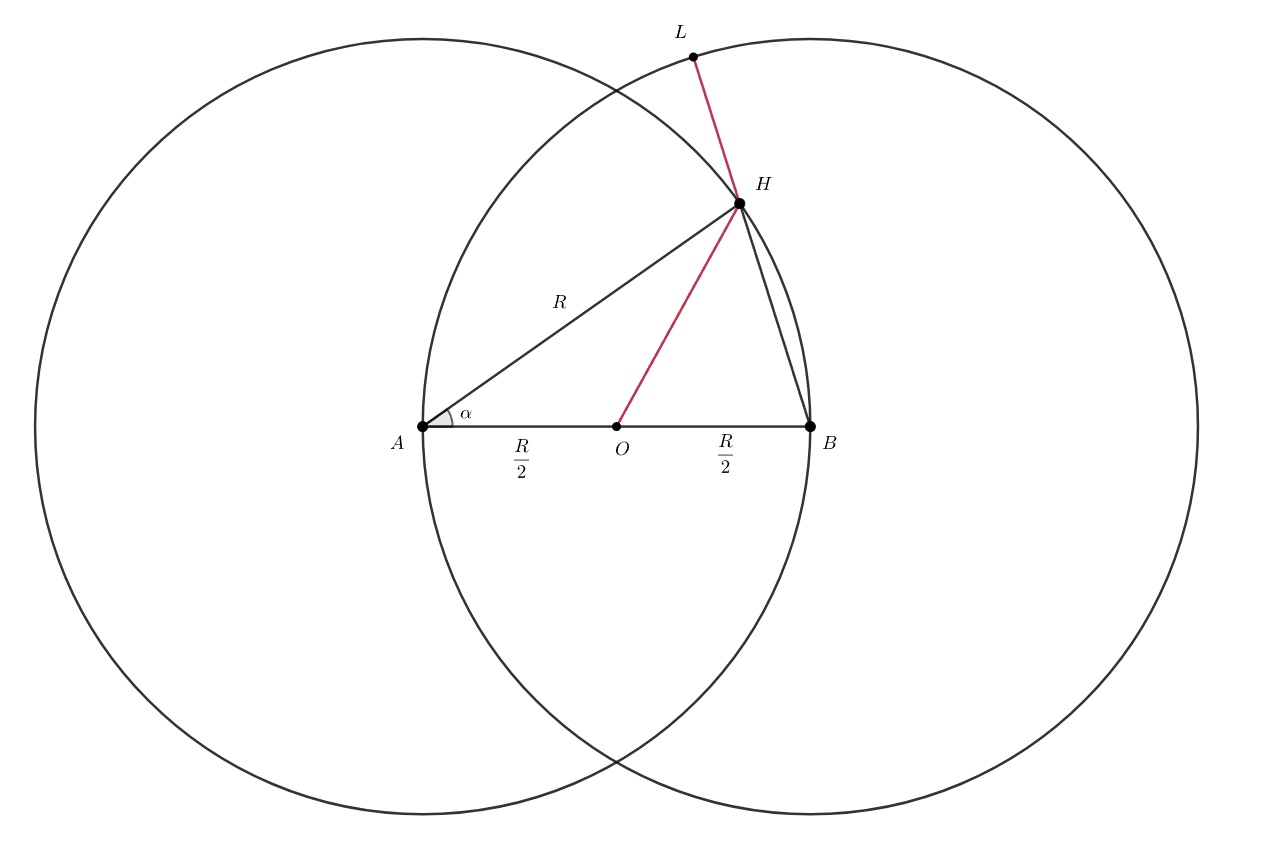
Мышь мокнет от каждой поливалки, поэтому нужно минимизировать сумму расстояний, пройденных под каждой поливалкой. Путь под поливалкой $A$ равен $|OH |,$ путь под поливалкой $B$ равен $|OH |+ |HL |,$ поэтому нужно найти минимально возможное значение $|OH|+ (|OH |+ |HL|)=2|OH|+ |HL |.$

Опишем положение $H$ через угол $∠HAB =α,$ где $α ∈[0,60∘].$

Тогда:

|AH|= R, |OA|= R- 2

По теореме косинусов:

∘ --------------- R2 |OH |= R2+ -4-− R2cosα

Далее, $|HL |= R− |BH |,$ а $|BH |$ найдём как основание равнобедренного треугольника с боковыми сторонами $R$ и известным углом между ними:

|HL |= R − 2R ⋅sinα 2

Значит:

( ∘ ------- ) 2|OH |+|HL|= f(α )=R 2 5− cosα +1− 2sin α-, где α∈ [0,π] 4 2 3

Нужно найти минимум функции $f(α),$ которая характеризует степень намокания — берём производную:

( ) α ′ | α sinα | R cos 2- ( ∘ 5------ α ) f (α)= R |(− cos2-+ ∘5-----|) = ∘-5------ − 4 − cosα+ 2sin2 4 − cosα 4 − cosα

Нулю может равняться только скобка (угол $α$ меняется в таких пределах, что $α cos2-$ в ноль не обращается). Решаем уравнение:

∘------- 2sinα-= 5− cosα 2 4

4sin2 α= 5 − cosα 2 4

2 − 2cosα= 5− cosα 4

cosα = 3 4

Если $cosα = 3, 4$ то $sin α-= √1- 2 2 2$

Значит, экстремум $f$ равен:

( √2) f(α)= R ⋅ 1+ 2--

На всякий случай проверим, точно ли это точка минимума. Если бы мышь взяла курс ровно наверх, то $f(α)$ приняла бы значение $√3 √ - 2R ⋅2--=R 3,$ что больше, чем $( √2) R ⋅ 1+ -2- .$ Если бы побежала направо — $f(α)$ равнялось бы $2R.$ Так что мы действительно нашли минимум.

Длина пути при этом равна:

( ∘------- ) ( ∘-- ) |OH |+|HL|= R 5 − cosα+ 1− 2sinα = R 1+ 1− √2- =R = 4− 2√2 4 2 2 2 2

Ответ:

$4− 2√2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#125184Максимум баллов за задание: 7

Первооткрыватель летел над джунглями на вертолёте и заметил забытый храм инков. Храм выстроен в форме правильной усечённой пирамиды с квадратными основаниями сторона нижнего основания равна 2048 и.е., сторона верхней площадки равна 486 и.е. (и.е. инкские единицы длины). Высоту храма путешественник измерить не сумел, поэтому посадил вертолёт на верхней площадке и начал спускаться по боковой поверхности пирамиды, начиная от угла. Спускался он не напрямую — склон для этого слишком крут — а наискосок, по линии, угол наклона которой к поверхности земли равен $∘ 45.$ Когда он добирался до бокового ребра, он переходил через ребро и шёл по следующей грани, под таким же углом $∘ 45$ к поверхности земли.

Он закончил спуск ровно у вершины нижнего основания пирамиды, насчитав по пути 5 сторон (иными словами, его путь выглядит как ломаная, и в этой ломаной получилось 5 отрезков). Какой высоты (в и.е.) был храм?

Источники: Ломоносов - 2025, 11.7 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть сторона нижнего основания пирамиды равна a, сторона верхнего — b, угол спуска равен α, число пройденных граней равно n. Попробуйте ввести и выразить неизвестные. Что мы хотим найти?

Подсказка 2

Нас интересует высота храма. Обозначим ее за H. Через какой угол ее можно выразить?

Подсказка 3

Обозначим угол наклона боковой стороны пирамиды к земле через β. Выразите H через tg(β).

Подсказка 4

H = (a - b) ⋅ tg(β) / 2. Далее будем считать, что первооткрыватель поднимался, а не спускался. Что можно сказать о линиях, по которым двигался первооткрыватель?

Подсказка 5

Из подобия, первооткрыватель будет проходить по каждой грани меньшее расстояние. Будем считать, что переход по следующей грани будет равен некоторому q, умноженному на длину перехода по предыдущей грани. Какие подобные фигуры мы получим на гранях?

Подсказка 6

У нас получатся подобные трапеции с основаниями a и aq, aq и aq², aq² и aq³ и т.д.. У последней трапеции верхнее основание будет равно b, выразите q.

Подсказка 7

Так как b = aqⁿ, то q = (b / a)¹ᐟⁿ. Обозначьте высоту, на которую первооткрыватель поднялся по первой трапеции, за h. Выразите через эту величины H.

Подсказка 8

H = h + qh + ... + qⁿ⁻¹h. Найдите сумму геометрической прогрессии.

Подсказка 9

Она будет равна (h(a-b)) / (a(1-q)). Заметим, что в этом выражении нам известно все, кроме h. Введем обозначения: ребро, с которого начался подъем — AB, путь начат из A, первый отрезок пути соединяет точки A и P на боковом ребре. Из точки P проведем в плоскости ABP прямую, параллельную AB, она пересечет другое боковое ребро в точке P₁. Получим трапецию с основаниями a и aq. Попробуйте сделать некоторые построения и выразить h.

Подсказка 10

Ортогонально спроецируем точку P на основание пирамиды, получим точку R, тогда PR = h. Попробуйте выразить h через некоторый треугольник.

Подсказка 11

От точки R в плоскости основания проведите перпендикуляр к AB, пусть у нас получится точка L на AB.

Подсказка 12

Заметим, что ∠RBA = 45°, так как R падает на диагональ квадрата, являющегося основанием пирамиды. Что из этого следует?

Подсказка 13

Тогда LB = LR. Выразите h через LR.

Подсказка 14

LR = h / tg(β). Что еще можно заметить в треугольнике ALR?

Подсказка 15

AR = h / tg(α), AL = a - h / tg(β). А еще этот треугольник - прямоугольный. Запишите для него теорему Пифагора.

Подсказка 16

Можно решить квадратное уравнение относительно 1/h.

Подсказка 17

1/h = (1 / (a⋅tg(β))) ⋅ (1 + 1/tg(α) ⋅ √(tg²(β) - tg²(α))). Можем ли мы воспользоваться одним из свойств трапеции?

Подсказка 18

LB = 1/2 ⋅ (AB - PP₁). Подставьте известные нам величины.

Подсказка 19

В итоге получим, что 1/h = 2 / (a ⋅ (1 - q) ⋅ tg(β)). Но мы ведь и до этого получали 1/h.

Подсказка 20

Тогда 1/h = (1 / (a⋅tg(β))) ⋅ (1 + 1/tg(α) ⋅ √(tg²(β) - tg²(α))) = 2 / (a ⋅ (1 - q) ⋅ tg(β)) = 1/h.
Получим, что tg(β) = tg(α) ⋅ √((2(1+q²) / (1-q)²). Вспомните, чему равняется H.

Подсказка 21

Так как H = h(a-b) / (a(1-q)), h = a⋅(1-q)⋅tg(β)/2, и мы нашли tg(β), можем выразить H и подставить значения из условия задачи.

Показать ответ и решение

Пусть сторона нижнего основания пирамиды равна $a,$ сторона верхнего равна $b,$ угол спуска равен $α,$ а число пройденных граней равно $n.$

$PIC$

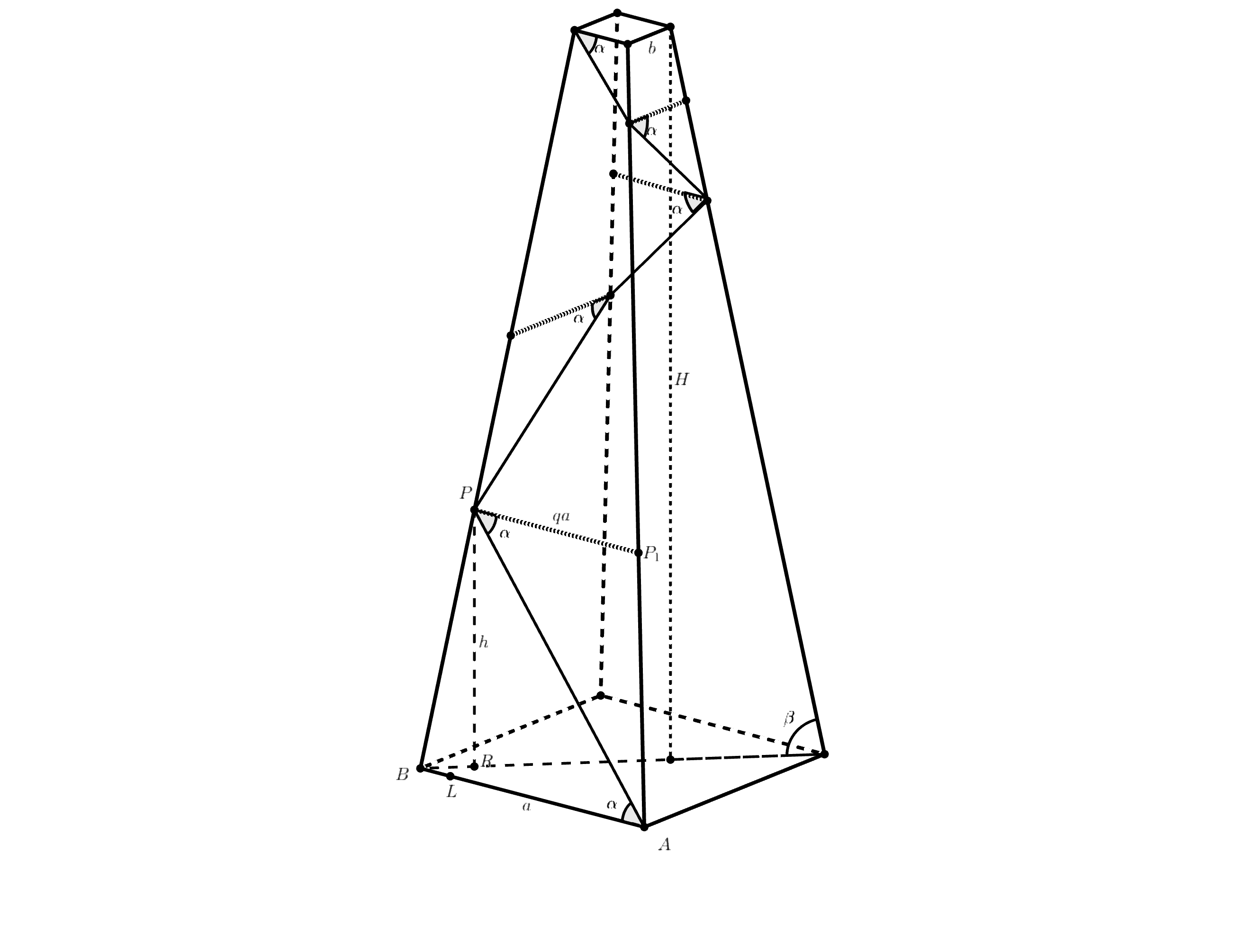
Будем считать, что первооткрыватель поднимался. Обозначим (пока неизвестные нам) величины — высоту постройки через $H,$ угол наклона боковой стороны пирамиды к земле через $β.$ Тогда

2H tg(β)= a− b

H = a− b-tg(β) 2

Посмотрим на пирамиду в проекции сверху.

$PIC$

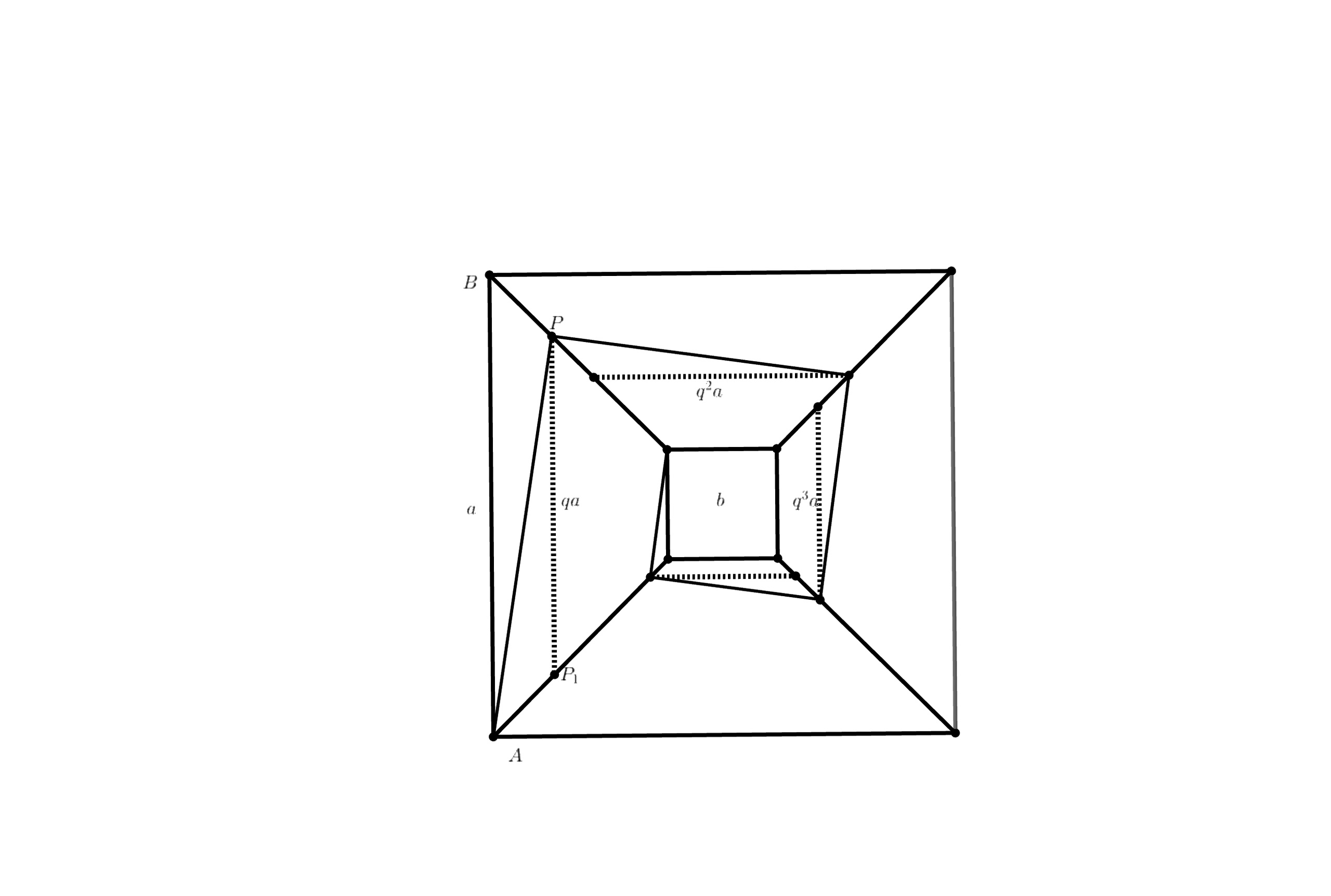
Заметим, что рисунки на гранях подобны друг другу — поднимаясь, первооткрыватель будет проходить по каждой грани все меньшее расстояние, при том переход по следующей грани будет равен некоторому $q,$ умноженному на длину перехода по предыдущей грани.

У нас есть трапеции с основаниями $a$ и $qa,$ $qa$ и $q2a,$ $q2a$ и $q3a,$ и так далее. У последней трапеции верхнее основание будет равно $b,$ следовательно,

n∘-b b= qna;q = a

Обозначим высоту, на которую первооткрыватель поднялся по первой трапеции, за $h.$ Тогда из подобия следует, что за второй переход он добавит к высоте $qh,$ за третий — $q2h,$ и так далее. Тогда

1− qn 1 − b h(a− b) H = h+qh +q2h+ ...+ qn−1h= h-1−-q =h-1−a q-= a(1− q)

Нам известны все величины, кроме $h.$

Обозначим на пирамиде некоторые точки. Ребро основания, с которого начат подъем — это $AB,$ путь начат из $A.$ Первый отрезок пути соединяет точки $A$ и $P$ на боковом ребре.

Из точки $P$ проведем в плоскости $ABP$ прямую, параллельно $AB,$ она пересечет другое боковое ребро в точке $P1.$ Получится трапеция $ABPP1$ с основаниями $AB = a,$ $PP1 = qa.$ Точку $P$ ортогонально спроецируем на основание пирамиды — получим точку $R,$ $PR =h.$ От точки $R$ в плоскости основания пирамиды проведем перпендикуляр к $AB,$ он пересечет $AB$ в точке $L.$

Тогда угол $RBA$ равен $45∘,$ так как R падает на диагональ квадрата, являющегося основанием пирамиды. $RL= LB,$ а

LR = -h-- tg(β)

Кроме того,

h h AR = tg(α);AL= a− tg(β)

Треугольник $ALR$ прямоугольный, поэтому

( h )2 ( h )2 ( h )2 tg(α) = tg(β) + a− tg(β)

Решим квадратное уравнение относительно $1h.$

( )2 ( ) a2 1 − -2a--⋅ 1+ 2tg22(α-)− tg22(β) =0 h tg(β) h tg (β)⋅tg(α)

Положительным решением будет

1 --1--( --1-∘ -2------2--) h = atg(β) 1+ tg(α) tg (β)− tg (α)

По свойствам трапеции

1 LB =2 (AB − PP1),

то есть

a(1− q)=2hctg(β)

h= a(1− q)tg(β) 2

1= -----2---- h a(1− q)tg(β)

Тогда

2 1 ( 1 ∘--2-----2--) a(1−-q)tg(β) = atg(β) 1+ tg(α) tg(β)− tg (α)

∘------------ -2--= 1+ -1-- tg2(β)− tg2(α) 1− q tg(α)

∘ 2(1+-q2) tg(β) =tg(α) (1−-q)2-

Вспомним, что

H = h(a−-b) a(1− q)

Так как

a(1 − q) h= --2---tg(β),

можем подставить $tg(β).$ Получим

√- ∘ ------- H = -2(a− b) 1-+q2-tg(α), 2 (1 − q)2

где

∘-b q = n a

По условию, $a =2048,$ $b= 486,$ $n= 5,$ $α =45∘.$ В итоге $H = 3905√2.$

Ответ:

$3905√2$

Ошибка.
Попробуйте повторить позже

Задача 8#125185Максимум баллов за задание: 7

Через три стороны правильного 30-угольника проводят прямые. Стороны выбирают так, что прямые пересекаются друг с другом, и исходный многоугольник лежит внутри полученного треугольника.

Сколько попарно неравных треугольников может получиться? Равными считаются треугольники, которые можно совместить поворотом или отражением.

Источники: Ломоносов - 2025, 11.8 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть чётное n — число сторон многоугольника. Сколько есть способов выбрать тройку его сторон (a,b,c)?

Подсказка 2

n⋅(n-1)⋅(n-2). Но ведь не любые 3 стороны образуют треугольник, к тому же, разные тройки могут порождать одинаковые по форме фигуры. Какие фигуры нам надо различать для правильного подсчёта?

Подсказка 3

Нам понадобится различать равносторонние, равнобедренные и прочие треугольники, так как у них разное количество симметрий. Давайте считать, что (a,b,c) расположены против часовой стрелки. Попробуйте посчитать количество треугольников.

Подсказка 4

a можно выбрать n способами, теперь пометим параллельную a сторону красным. Сколько есть вариантов для выбора b?

Подсказка 5

Для выбора b отсчитываем k сторон от a, где k = {0;1;2;...;(n-2)/2 - 1}. Пометим параллельную b сторону синим. Сколько есть вариантов для выбора c?

Подсказка 6

Для выбора c останутся только стороны между красной и синей — получится ровно k вариантов. Сколько всего треугольников получится? Не забудьте учесть случаи, когда (a,b,c) расположены по часовой стрелке.

Подсказка 7

Получится n ⋅ (0 + 1 + 2 + ... + (n-2)/2 - 1) ⋅ 2/6 с учетом расположения по часовой стрелке и исключением перестановок. Преобразуйте выражение.

Подсказка 8

S = n⋅(n-2)⋅(n-4)/24. Теперь посчитайте количество равнобедренных (но не равносторонних) треугольников.

Подсказка 9

Выберем основание n способами. Под каким углом к основанию можно выбрать правую боковую сторону?

Подсказка 10

Она должна пересекаться с основанием под острым углом (но не 60°). Что можно сказать про левую боковую сторону?

Подсказка 11

она будет достроена однозначно. Сколько есть вариантов выбрать правую боковую сторону?

Подсказка 12

Есть (n-4)/4 вариантов, если n делится на 4, и (n-2)/2 - в ином случае. Также нужно учесть случай, когда угол равен 60°. При каком n будет такая боковая сторона?

Подсказка 13

Такая сторона будет, если n кратно 3. Теперь разберите все возможные случаи для равнобедренных (но не равносторонних) треугольников.

Подсказка 14

Когда можно выбрать равносторонний треугольник?

Подсказка 15

Из рассуждений о равнобедренных треугольниках, когда n кратно 3. Разберите случаи.

Подсказка 16

Сколько будет неравнобедренных треугольников?

Подсказка 17

Из общего количества треугольников нужно вычесть количества равнобедренных и равносторонних. Теперь учтите повороты и отражения для каждого типа.

Показать ответ и решение

Пусть $n$ — число сторон многоугольника. Пусть $n$ чётное. Всего способов выбрать тройку сторон $(a,b,c)$ из имеющихся $n$ будет $n(n− 1)(n− 2).$ Правда, не каждая тройка порождает треугольник, и разные тройки могут порождать одинаковые по форме фигуры. Для правильного подсчёта нам понадобится различать равносторонние, равнобедренные и остальные треугольники, так как у них разное количество симметрий.

$PIC$

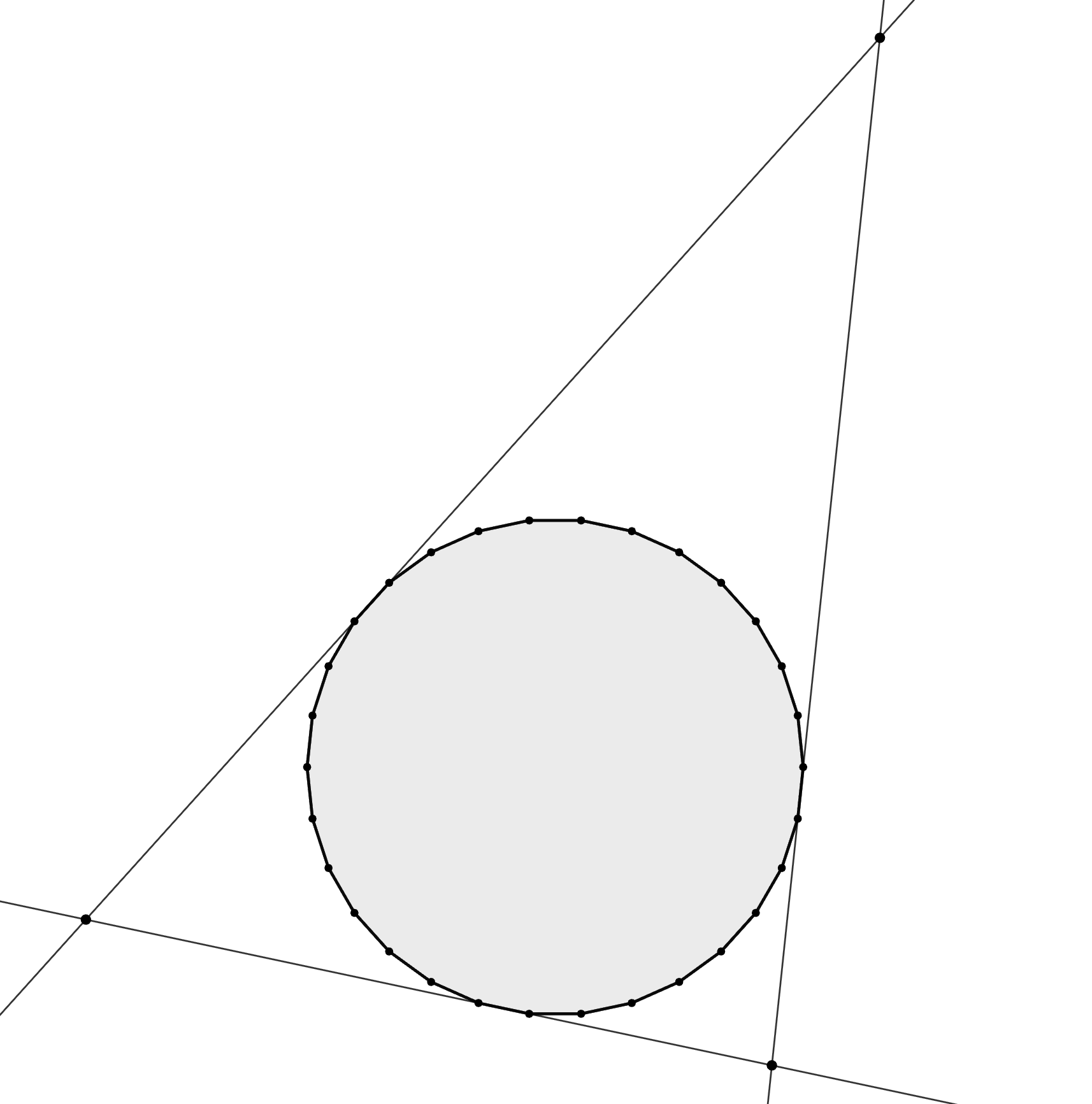
Давайте считать, что $(a,b,c)$ расположены против часовой стрелки. Первую сторону треугольника $a$ можно выбрать $n$ способами. Пометим параллельную $a$ сторону красным. Для выбора второй стороны $b$ отсчитываем $k$ сторон от $a,$ где $n−2 k= 0,1,2,...,-2- − 1.$ Помечаем параллельную $b$ сторону синим. Для выбора c остаются только стороны между красной и синей сторонами –— и вариантов выбора будет ровно $k.$ Значит, всего треугольников будет $n⋅(0+1 +2+ ...+ n−22− 1)⋅ 26$ (умножаем на $2,$ чтобы учесть тройки, где $a,b,c$ расположены по часовой, и делим на $6$ для учёта всех перестановок $a,b,c$ между собой). Используем формулу суммы прогрессии, получаем, что всего треугольников будет

S = n(n-− 2)(n-− 4)- 24

Посчитаем, сколько будет равнобедренных (но не равносторонних) треугольников. Основание можно выбрать $n$ способами, правую боковую сторону выбираем так, чтобы она пересекалась с основанием под острым углом (но не $60∘).$ Левая боковая сторона будет достроена однозначно. Для выбора боковой стороны есть $n−44$ вариантов (если $n$ делится на $4),$ и $n−22$ в ином случае, и ещё нужно отнять одну сторону под углом $60∘,$ которая будет, если $n$ делится на $3.$ Равнобедренных треугольников будет ( $m,q$ — целые)

1.: $S2 = n(n4−4),$ если $n =4m,n ⁄=3q$
2.: $S2 = n(n4−2),$ если $n ⁄=4m,n ⁄=3q$
3.: $S2 = n(n−8), 4$ если $n =4m,n =3q$
4.: $S2 = n(n−6), 4$ если $n ⁄=4m,n = 3q$

Равносторонний треугольник можно выбрать, если $n$ делится на $3.$ Таких треугольников будет $n 3$ штук. Если $n$ на $3$ не делится, то их не будет.

1.: $S3 = n , 3$ если $n = 3q$
2.: $S3 =0,$ если $n⁄= 3q$

Значит, у нас есть $S1 = S− S2− S3$ неравнобедренных, $S2$ равнобедренных неравносторонних и $S3$ равносторонних треугольников.

Теперь учтём повороты и отражения. Равносторонний треугольник на самом деле единственный. Каждый равнобедренный (но не равносторонний) треугольник имеет $n$ равных себе, полученных поворотами. Неравнобедренный треугольник можно поворачивать $n$ способами и отражать, что даёт $2n$ равных ему.

Значит, ответ (в общем случае при чётном $n$ ) равен:

S− S2− S3 S2 3S3 ---2n----+ n-+ -n-

А при $n= 30$ ответ равен $19.$

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 9#129843Максимум баллов за задание: 7

Решите неравенство

∘--------------∘-------------- log22x+3 log2x− log22x +3log2 x− 4 ≥log2x +1

В ответ запишите сумму всех целых значений функции $f(x0)= 16x0,$ где $x0$ — решение неравенства.

Источники: Ломоносов - 2025, 10.1 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Нам никак не избежать нахождения х₀, значит, придётся решать неравенство. Замена просится сразу, но что же делать дальше? Если простые пути не ищутся, можно попробовать решить "в лоб" равносильными переходами!

Подсказка 2

Запишем ограничения для переменной после замены, посмотрев на внутренний корень. Заметим, что в одном из полученных интервалов всё однозначно и просто: мы возводим в квадрат, приводим подобные, потом ещё раз внимательно проверяем все ограничения, и кусочек ответа готов!

Подсказка 3

Со второй частью посложнее. Тут придётся разобраться с большим подкоренным выражением. Как это неравенство привести к неравенству четвёртой степени понять не слишком сложно, но вот как его решить?

Подсказка 4

С одной стороны, напрашивается замена, с другой, можно просто сделать красивую группировку, представив наш многочлен в виде суммы двух неотрицательных выражений. Осталось лишь провести обратную замену и понять, какие значения принимает f(x) на полученном промежутке!

Показать ответ и решение

Решение:

Сделаем замену переменных $t= log2x.$ Получим:

2 ∘ -------- t +3t− t2+3t− 4≥ t+1

Из условия $t2+ 3t− 4≥ 0$ следует, что $t≥ 1$ и $t≤− 4.$ Если $t≥ 1,$ то можно возвести в квадрат

2 ∘ -2------ 2 t+ 3t− t +3t− 4≥ t+ 2t+1

∘t2+-3t− 4-≤t− 1

Из ограничений на правую часть неравенства следует, что $t≤ 1.$ Значит может подойти только $t=1.$ Проверка:

√1+-3−-4= 1− 1

0= 0

Если $t≤− 4,$ то неравенство будет выполняться всегда, при условии

∘-------- t2+3t− t2+ 3t− 4≥ 0

4 3 2 t +6t + 8t − 3t+4≥ 0

t2(t2+ 6t+ 8)+(4− 3t)≥ 0

Выражение в первых скобках неотрицательно при условии $t≤ −4.$ Выражение во вторых скобках положительно при всех отрицательных $t.$ То есть, неравенство выполняется для всех значений переменной из промежутка $t≤ −4.$ Таким образом,

t∈{1}∪(−∞; −4]

x∈ (0;2−4]∪{2}

Рассмотрим функцию $f(x)= 24x.$ При $x∈ (0;2−4],$ функция принимает значения с промежутка $(0;1].$ Если $x= 2,$ то $f(x)=25.$ Итак, искомая сумма равна $1 +25 = 33.$

Ответ: 33

Ошибка.
Попробуйте повторить позже

Задача 10#129844Максимум баллов за задание: 7

Биссектрисы треугольника $ABC$ пересекаются в точке $O.$ Прямая $AO$ пересекает описанную окружность треугольника $OBC$ в точках $O$ и $M.$ Найдите длину секущей $OM,$ если $BC =6,$ $AB :AC = 3:1$ и $∘ ∠BAC = 60 .$

Источники: Ломоносов - 2025, 10.2 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Небольшой счёт углов и знание теоремы синусов помогут нам сразу же узнать радиус имеющейся на рисунке окружности. Но как нам связать его с искомым отрезком?

Подсказка 2

Попробуем вычислить угол, опирающийся на эту дугу! Поищите на рисунке равные уголочки и свяжите искомый угол с углами △ABC.

Подсказка 3

Осталось лишь вспомнить свойство вписанного угла, равного 90°, и записать ответ!

Показать ответ и решение

$PIC$

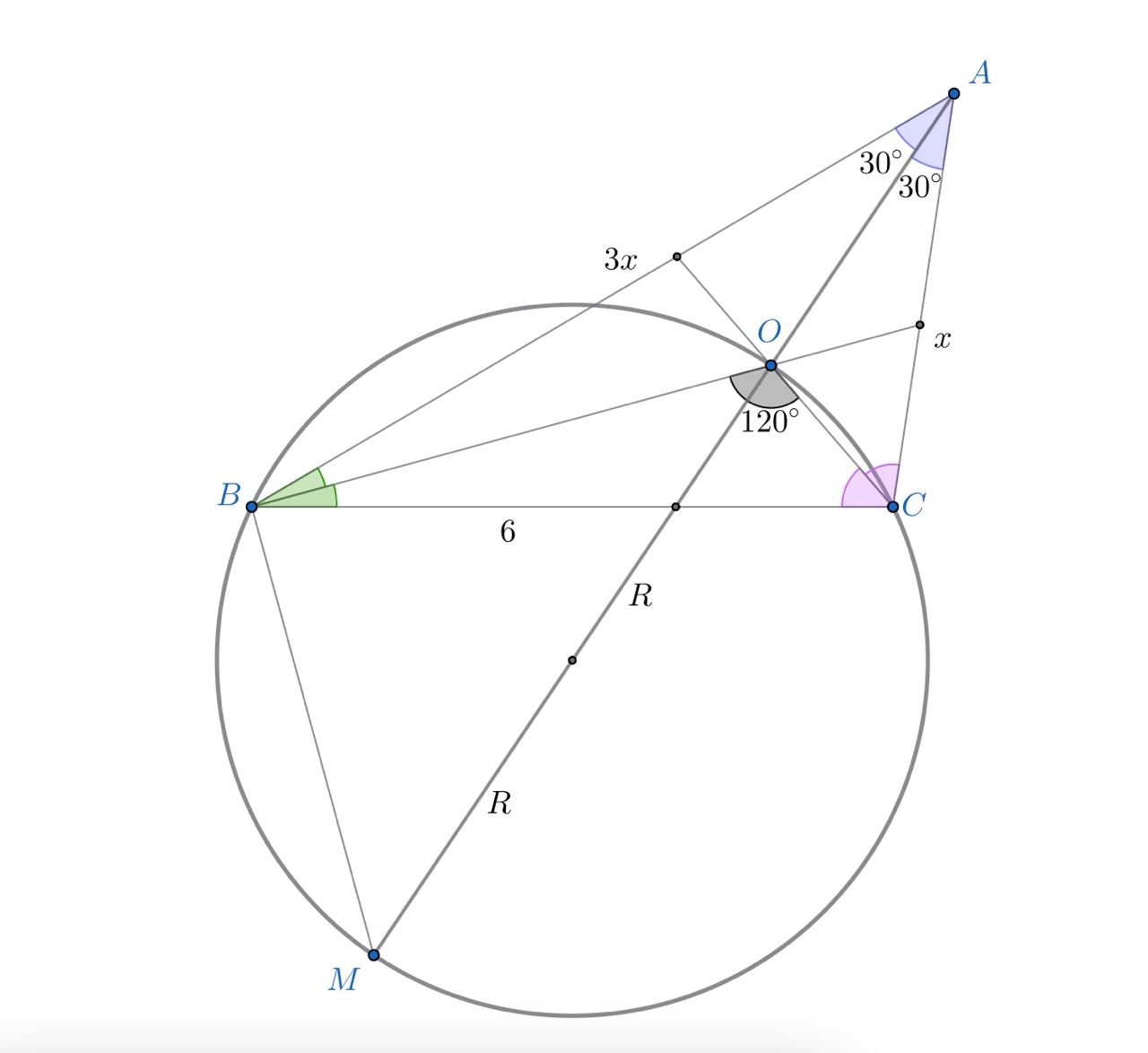
Заметим, что

∠OBM = ∠ABC- +∠CBM = ∠ABC- +∠COM = ∠ABC-+ ∠OAC + ∠OCA = ∠ABC-+-∠BAC-+-∠ACB-= 90∘ 2 2 2 2

Значит, $OM = 2R,$ где $R$ — радиус описанной около треугольника $OBC$ окружности.

Также

∠BOC = 180∘− ∠B-+-∠C =180∘− 180∘−-∠A-= 90∘ + ∠A-= 120∘ 2 2 2

Поэтому, по теореме синусов:

BC √6⋅2 √- OM = 2R =sin120∘ = -3--= 4 3

Ответ:

$4√3$

Ошибка.
Попробуйте повторить позже

Задача 11#129847Максимум баллов за задание: 7

Решите неравенство

∘ √-------√------ ∘ √------√------ cosx+ 2 −3sinx > 2 cosx− −3sin x

Источники: Ломоносов - 2025, 10.3 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Итак, у нас сравнение двух не самых красивых корней... С чего мы обычно начинаем решать подобные штуки? Подумайте: есть ли какое-то условие в ОДЗ, которое выполняется автоматически?

Подсказка 2

С двумя простыми условиями, ограничивающими косинус и синус, всё в целом понятно — они выделяют нам четверть на тригонометрической окружности, но что делать с последним?

Подсказка 3

Его, конечно, можно решить, но что, если в исходном неравенстве избавиться от внешних корней и привести подобные?

Подсказка 4

Исходное неравенство примет вид сравнения корня из cos(x) с корнем из (-3sin(x)), умноженным на какой-то коэффициент. Попробуйте перейти к двойному неравенству.

Подсказка 5

Тут уже много путей для решения! Один из них — поделить выражение на корень из косинуса и работать с тангенсами. Только не забудьте обосновать, почему мы имеем право так делать!

Подсказка 6

Вот и всё! Осталось проверить, что для таких тангенсов выполняется ОДЗ, а также не испугаться аркфункций в ответе.

Показать ответ и решение

Запишем ОДЗ:

(| cosx ≥0 { −3sinx ≥0 |( √---- √------ cosx− −3sinx ≥ 0

Первое и второе неравенства из ОДЗ выполняются в 4 четверти тригонометрической окружности, т.е. $x ∈[− π +2πn;0+ 2πn],n ∈ℤ. 2$

Так как левая и правая части исходного неравенства неотрицательные, можем возвести их в квадрат:

√---- √------ √---- √ ------ cosx +2 − 3sinx> 4 cosx− 4 −3sinx

3√cosx-<6√ −3sinx-

√cosx< 2√−3-sinx

С учетом 3 неравенства ОДЗ получим

√−3sin-x≤ √cosx< 2√ −3sinx-

Если $cosx =0,$ то $sinx= −1,$ так как ОДЗ находится в 4 четверти, тогда 3 неравенство из ОДЗ обращается в

√- 0≥ 3

Следовательно, $cosx ⁄=0.$ Можем поделить на $√---- cosx:$

∘ ----- ∘ ----- −3tg x≤ 1< 2 −3tgx

1 ∘ ----- 2 < −3tgx≤ 1

1 1- − 3 ≤ tgx < −12

1 1 − arctg3 +2πn ≤x <− arctg12 + 2πn,n ∈ℤ

3 неравенство из ОДЗ было учтено, а также полученные $x$ лежат в 4 четверти, поскольку тангенс монотонно возрастает на промежутках $[ ] − π2 + 2πn;π2 + 2πn ,$ $n ∈ℤ,$ на отрезках $[ ] 0+2πn;π2 +2πn ,$ $n∈ ℤ$ принимает значения $(0;+ ∞),$ а мы берем с минусом углы, при который тангенс получается равным $13$ и $112,$ следовательно, это ответ.

Ответ:

$− arctg 1 +2πn≤ x< − arctg 1-+2πn,n∈ ℤ 3 12$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#129848Максимум баллов за задание: 7

При каких значениях параметра $a$ уравнение

x x |x+ 1− a|+ |4 − a|=4 − x− 1

имеет на промежутке $[−1;1]$ единственное решение?

Источники: Ломоносов - 2025, 10.4 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

А можно ли как-то преобразовать исходное равенство?

Подсказка 2

Попробуйте получить слева и справа одинаковые части.

Подсказка 3

Например, добавив и отняв справа а, можно получить 4ˣ - a.

Подсказка 4

В итоге имеем равенство вида |s| + |t| = s + t. Когда оно выполняется?

Подсказка 5

Раскрывая модули, можно получить неравенства для a и построить графики в координатах xOa. Не забудьте учесть, что нам нужно единственное решение на промежутке [-1;1]!

Показать ответ и решение

Наше уравнение может быть записано в виде

x x |a− x − 1|+ |4 − a|= (4 − a)+ (a− x − 1)

и, если к нему добавить условие попадания $x$ в промежуток $[−1;1],$ равносильно системе неравенств

(| a≥ x+ 1 { a≤ 4x |( −1 ≤x ≤1

Рассмотрим множество, которое задаётся этими неравенствами на плоскости с координатами $x$ и $a.$

$PIC$

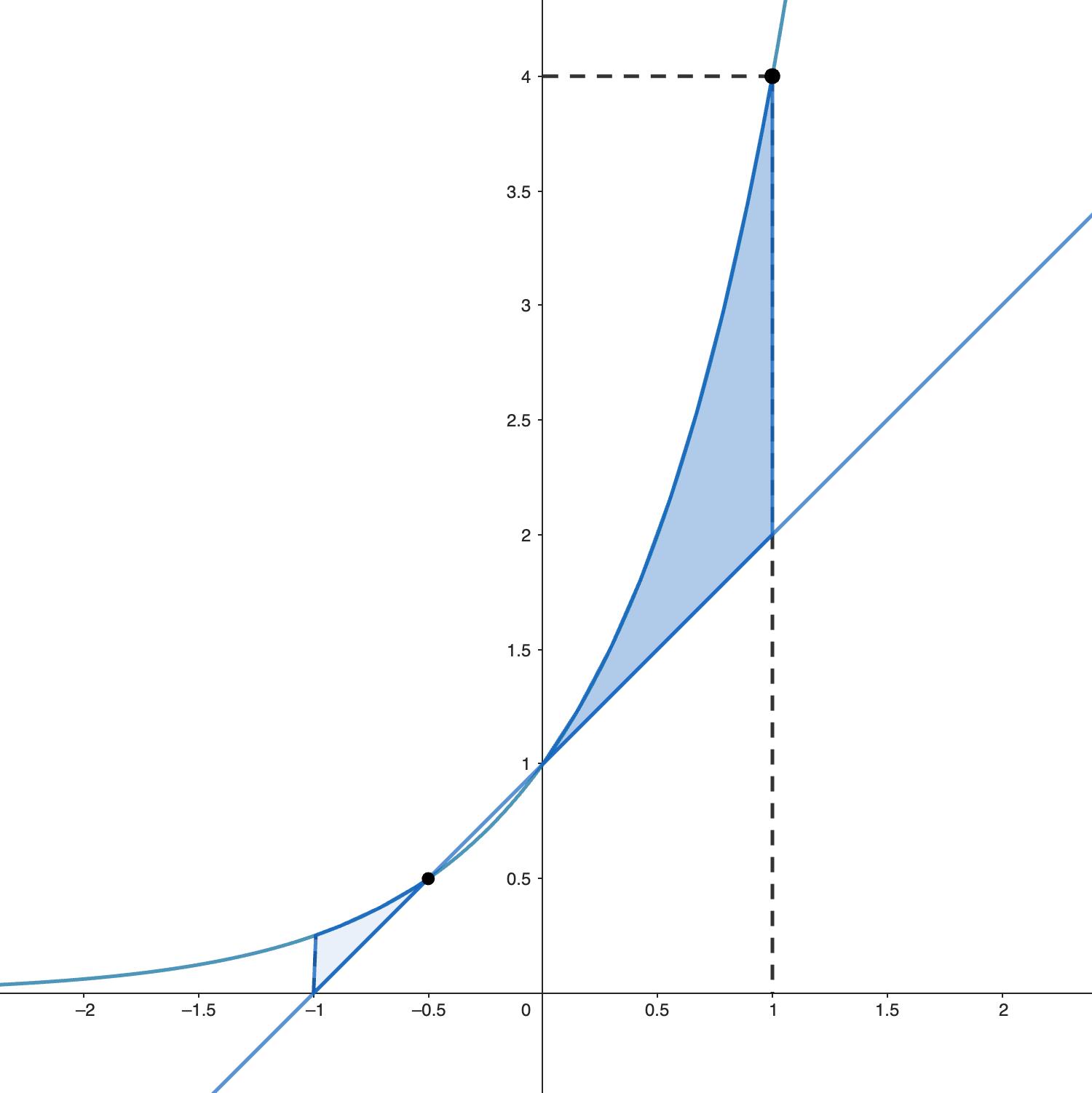
Графики функций $y = x+ 1$ и $y = 4x$ пересекаются в двух точках: $(0;1)$ и $(−0.5;0.5).$ Функция $y = 4x$ выпукла вниз, поэтому при $x ∈[−1;− 0.5]∪[0;1]$ она больше функции $y = x+ 1,$ а при $x ∈[−0.5;0]$ — меньше. Каждому $a$ соответствует одна горизонтальная прямая на плоскости, и нас интересует, когда эта прямая пересекается с рассматриваемым множеством ровно в одной точке. Как видим, это имеет место при следующих значениях параметра $a$ : $0$ (при этом $x= −1$ ); $0.5$ (при этом $x =− 0.5$ ); $1$ (при этом $x= 0$ ); $4$ (при этом $x =1$ ).

Ответ:

${0;0.5;1;4}$

Ошибка.
Попробуйте повторить позже

Задача 13#129849Максимум баллов за задание: 7

На каждой стороне белого кубика сидит по жуку. Кубик бросили, и жуки переполошились — каждый выбрал наугад одну из 4-х соседних граней и переполз туда. С какой вероятностью кубик не изменит своего первоначального вида?

Источники: Ломоносов - 2025, 10.5 (см. olymp.msu.ru)

Показать ответ и решение

Если нарисовать на гранях кубика стрелки, направленные в сторону, куда пополз жук — мы тем самым опишем исход броска. Всего таких исходов будет $6 4 = 4096$ (6 граней, на каждой по 4 варианта), и они равновероятны.

Пример на развертке:

$PIC$

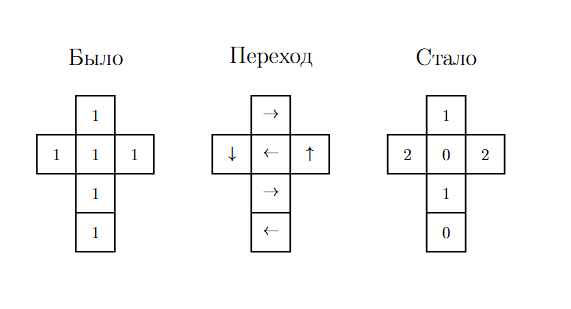
Рассмотрим исходы приведут нас к такому же кубику. На каждую грань должно вползать по одному жуку, то есть на каждую грань должна быть направлена ровно одна стрелка. Значит, если начать двигаться против направления стрелок — дорогу мы найдём однозначно, «развилок» не будет, и в конце концов, так как граней на кубике конечное число, мы будем вынуждены вернуться на грань, с которой начали. Это верно для любой грани. Иными словами, рисунок из стрелок образует на сторонах кубика цикл или несколько циклов.

Граней 6, поэтому длины циклов потенциально могут быть от 2 до 6. Циклы в 2, 3, 4 и 6 жуков нарисовать получится, а вот попытка нарисовать цикл длиной 5 приведёт к неподвижному жуку, так как жуки внутри цикла поменяются друг с другом местами, а последний не сможет переползти из своей грани, не оставив ее пустой. Значит, правильный исход может состоять из таких циклов: 2, 2, 2; 2, 4; 3, 3; 6. Посчитаем количество возможных рисунков с такими свойствами.

2, 2, 2 (то есть жуки попарно меняются местами). Жук с верхней грани меняется местами с жуком с одной из 4 боковых, а жуку с нижней остаётся всего 2 на выбор (он не может ползти на грань, противоположную выбранной верхним жуком). То есть таких конфигураций $4⋅2= 8.$
2, 4. Цикл длиной 4 обходит вокруг ребра куба — по или против часовой стрелки. Оставшиеся два жука меняются местами. Значит, число таких конфигураций равно числу способов выбрать ребро (рёбер 12) умножить на 2 (по или против часовой). Значит, $12⋅2 =24.$
3, 3. Цикл длиной 3 обходит вокруг вершины по или против часовой. Оставшиеся 3 жука ползут так же. Верхняя грань участвует в одном из циклов, значит мы можем выбрать для неё 4 соседние вершины, 2 ориентации, и ещё есть 2 ориентации для оставшихся жуков. Будет $4 ⋅2⋅2 =16$ рисунков.
6. Обойдём куб по направлению стрелок. С верхней грани мы можем перейти на одну из 4 боковых. Дальше мы можем повернуть налево, направо, или спуститься на нижнюю грань. Варианты «налево» и «направо» могут продолжится двумя способами: либо мы идём в ту же сторону, либо спускаемся вниз. Если мы шли в ту же сторону — дальше путь продолжается однозначно (через нижнюю грань), если спускались — вариантов дорисовывания 2. Вариант «на втором шаге мы спустились вниз» дорисовывается до полного цикла двумя способами.

Всего циклов длиной 6 будет $4(2(1+2)+ 2)=32.$ А вероятность равна

32+-16+24+-8 -80- -5- 4096 =4096 = 256

Ответ:

$-5- 256$

Ошибка.
Попробуйте повторить позже

Задача 14#129850Максимум баллов за задание: 7

На чертеже есть парабола и три точки $A,B,C.$ Из каждой точки к параболе проведены две перпендикулярные друг другу касательные. Расстояние от вершины $O$ параболы до прямой $AC$ равно 2. Найдите площадь треугольника $OAB,$ если $AC = 4,$ а $BC = 3.$

Источники: Ломоносов - 2025, 10.6 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Задачу приятно решать в координатах, но как их ввести, чтобы максимально упростить вычисления?

Подсказка 2

Конечно же, за начальную точку стоит взять вершину параболы — это позволит нам оставить только один коэффициент в её уравнении. Подумайте, как можно использовать условие о перпендикулярности касательных.

Подсказка 3

Если поработать с уравнениями касательных, можно понять, что они будут перпендикулярны лишь в том случае, если проведены из точек, лежащих на некоторой определённой прямой. А как нам помогают известные длины?

Подсказка 4

Неизвестный коэффициент найден благодаря расстоянию! Но однозначно ли взаимное расположение точек A, B и C? Осталось лишь воспользоваться формулой площади треугольника и получить ответ!

Показать ответ и решение

$PIC$

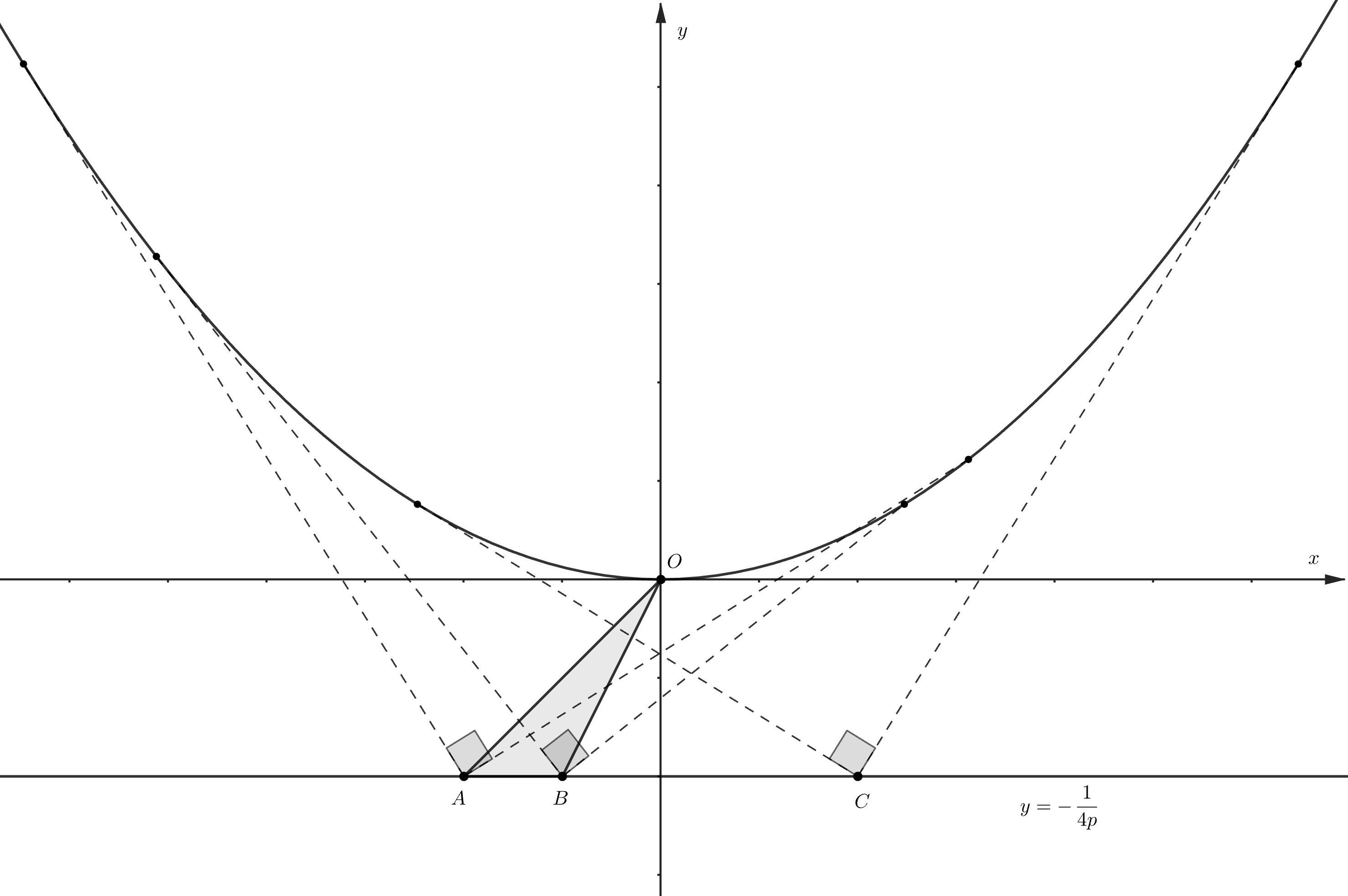
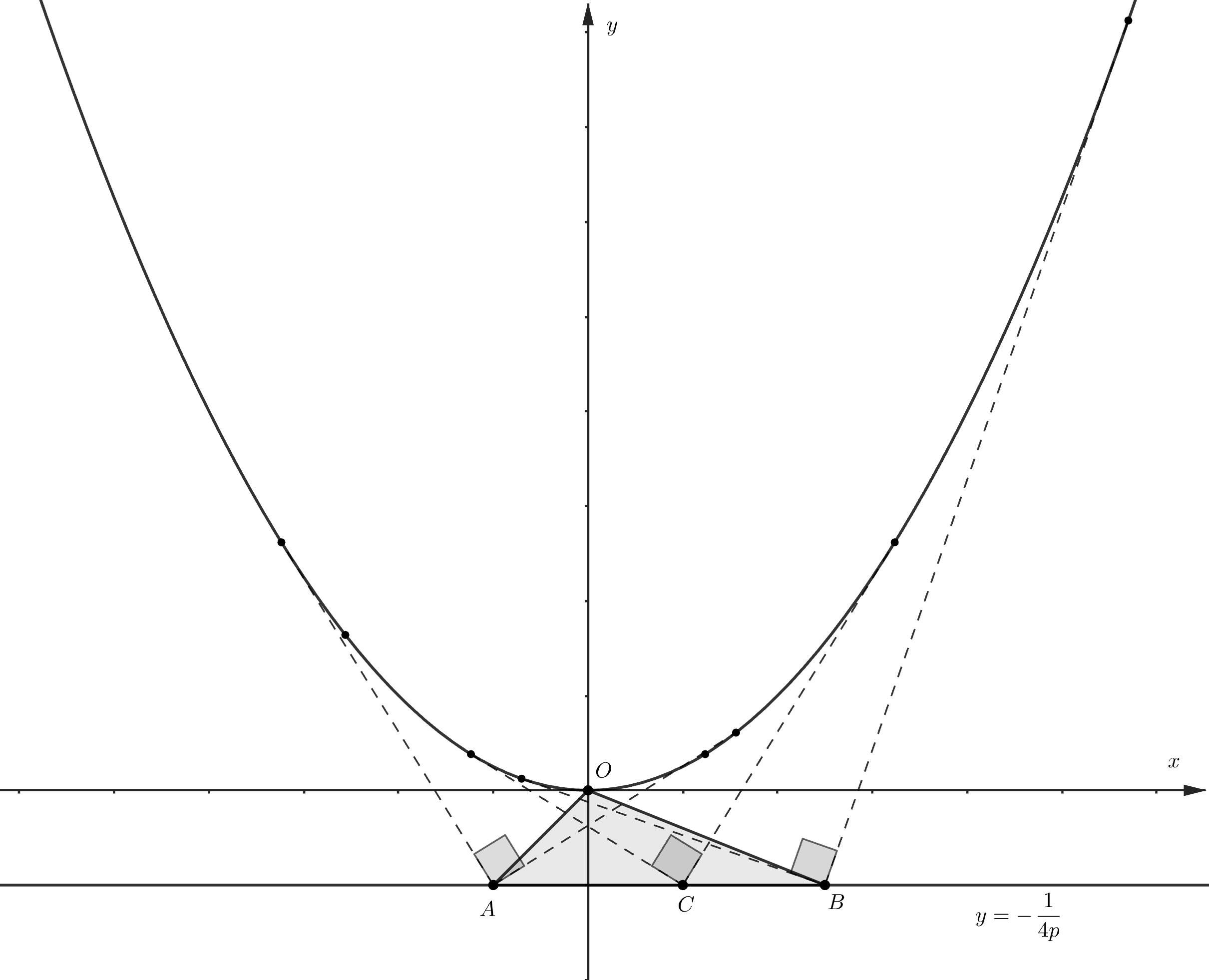
Пусть уравнение параболы $2 Π :y =px .$ Через точку $(x0,y0)$ проходит прямая $L :y =k(x− x0)+y0.$ Эта прямая будет касаться параболы в том случае, если она не параллельна оси параболы (т.е. $k ⁄=∞$ ) и имеет с параболой единственную общую точку — то есть уравнение

k(x − x0)+ y0 =px2

должно иметь единственное решение относительно переменной $x.$

Уравнение квадратное — значит, для единственности решения нужно, чтобы дискриминант равнялся нулю.

2 px − kx+(kx0− y0)= 0

Дискриминант этого уравнения равен

2 k − 4p(kx0 − y0)= 0

Он, в свою очередь, тоже образует квадратное уравнение, но для переменной $k.$

Угловые коэффициенты $k1,k2$ перпендикулярных прямых относятся так: $k1⋅k2 = −1.$ Значит, если из одной точки получилось провести перпендикулярные касательные к параболе, то уравнение имеет такие корни $k1,k2$ , что $k1⋅k2 = −1,$ а по теореме Виета это значит, что $4py0 = −1.$

То есть $y =− 1-, 0 4p$ и провести перпендикулярные касательные к параболе получится только из точек, лежащих на прямой $y = − 1-. 4p$ Точки $A,B,C$ лежат на одной прямой, и расстояние до этой прямой от точки $O$ известно из условия. Учитывая, что располагаться на прямой $A,B,C$ могут в разном порядке, мы получаем два возможных варианта ответа:

1⋅2⋅(4 +3)= 7 или 1⋅2⋅(4 − 3)= 1 2 2

Ответ: 1 или 7

Ошибка.
Попробуйте повторить позже

Задача 15#129852Максимум баллов за задание: 7

Назовем натуральное число счастливым, если все его цифры можно разбить на две группы, сумма цифр в каждой из которых одинакова. Примеры: 38221 (3+2+2+1=8); 5678 (5+8=6+7). Назовем число суперсчастливым, если оно счастливое и следующее за ним целое число тоже счастливое. Найдите количество суперсчастливых чисел на отрезке $[400;2400].$

Источники: Ломоносов - 2025, 10.7 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Какой по чётности должна быть сумма цифр счастливого числа? Помните, что мы должны уметь разбить его цифры на две группы с одинаковой суммой.

Подсказка 2

На какую цифру тогда заканчивается суперсчастливое число? Как правило, соседние числа имеют разные суммы цифр, если только не происходит переход через разряд.

Подсказка 3

Представьте разряды чисел при помощи переменных. Напишите условие на сумму цифр, сведя таким образом задачу к решению системы уравнений.

Подсказка 4

Чтобы проще было решать, рассмотрите отдельно трёхзначные числа, четырёхзначные с первой единицей, а также четырёхзначные с первой двойкой.

Показать ответ и решение

1) Рассмотрим трехзначные числа. Сумма цифр счастливого числа должна быть четной, иначе разбиение на две группы с одинаковой суммой цифр невозможно, поэтому суперсчастливое число должно заканчиваться цифрой $9,$ так как в ином случае суммы цифр двух последовательных чисел имеют разную четность. Значит, суперсчастливое трехзначное число имеет вид $--- ab9,$ а следующее за ним число состоит из цифр $a,b+ 1,0.$ Отметим, что при этом случай $b= 9$ невозможен, так как тогда число не будет счастливым.

Поэтому должны делиться на две группы с одинаковой суммой цифр как цифры $a,b$ и $9,$ так и цифры $a,b+1$ и $0.$ Для первой комбинации цифр или $a =b +9,$ откуда $a= 9,b= 0,$ или $b= a+ 9,$ что невозможно, или $a+ b= 9.$ Для второй комбинации $a =b+ 1.$

Одновременно оба числа счастливые только при $b= 4,a= 5.$ Таким образом, имеется одно трехзначное суперсчастливое число $549$ (за ним следует счастливое число $550).$

2) Рассмотрим четырехзначные числа. Аналогично предыдущему, суперсчастливое число должно заканчиваться цифрой $9$ . И также оно не может заканчиваться на $99,$ тогда сумма цифр двух последовательных чисел будет иметь разную четность, или на $999,$ тогда оно не будет суперсчастливым. Значит, искомое число имеет вид $---- abc9,$ где $a∈ [1,9],$ $b∈ [0,9],$ $c∈[0,8].$ Следующее за ним число состоит из цифр $a,b,c+1,0.$

Вначале рассмотрим случай $a= 1.$ Должны делиться на две группы с одинаковой суммой цифр как цифры $1,b,c$ и $9$ (назовем их первой комбинацией цифр), так и цифры $1,b,c+1$ и $0$ (назовем их второй комбинацией).

Для чисел второй комбинации возможны три ситуации (заметим, что не имеет значения, в какую группу включать $0$ ):

1= b+c+ 1 (то есть b= c= 0)

b= 1+c+ 1 (то есть b= c+ 2)

c+ 1= 1+ b (то есть b=c)

Для чисел первой комбинации вариантов гораздо больше, для уменьшения их количества подставим туда полученные выше три ситуации для второй комбинации.

Если $b= c=0,$ то комбинация $1,0,0,9$ счастливой не является.

Если $b= c+2,$ то получаются цифры $1,c+2,c$ и $9.$ Возможные варианты:

9 =1+ c+ 2+ c (тогда c =3)

9+ 1= c+ 2+ c (тогда c =4)

Получаются суперсчастливые числа $1539$ (за ним следует $1540$ ) и $1649$ (за ним следует $1650).$

Если $b= c,$ то получаются цифры $1,c,c$ и $9.$ Возможные варианты:

9= 1+c +c (тогда c= 4)

9+1 =c +c (тогда c= 5)

Получаются суперсчастливые числа $1449$ (за ним следует $1450$ ) и $1559$ (за ним следует $1560).$

Таким образом, в интервале $[1000,1999]$ есть $4$ суперсчастливых числа: $1449,1539,1559$ и $1649.$

3) Рассмотрим случай $a= 2.$ Должны делиться на две группы с одинаковой суммой цифр как цифры $2,b,c$ и $9$ (первая комбинация цифр), так и цифры $2,b,c+ 1$ и $0$ (вторая комбинация).

Для чисел второй комбинации возможны три ситуации:

2= b+c+ 1 (то есть b+ c= 1)

b= 2+c+ 1 (то есть b= c+ 3)

c+1 =2 +b (то есть b+ 1= c)

Если $b= c+1,$ то комбинация $2,b,c,9$ счастливой не является. Если $b= c+ 3,$ то получаются цифры $2,c+ 3,c$ и $9.$ Возможные варианты:

9 =2 +c+ 3+ c (тогда c= 2)

9 +2= c+ 3+ c (тогда c= 4)

Получаются суперсчастливые числа $2529$ (за ним следует $2530$ ) и $2749$ (за ним следует $2750).$

Если $c= b+1,$ то получаются цифры $2,b,b+ 1$ и $9.$ Возможные варианты:

9 =2 +b+ b+ 1 (тогда b= 4)

9 +2= b+ b+ 1 (тогда b= 5)

Получаются суперсчастливые числа $2349$ (за ним следует $2350)$ и $2569$ (за ним следует $2570).$

Таким образом, в интервале $[2000,2999]$ есть $4$ суперсчастливых числа: $2349,2529,2569$ и $2749.$ Всего на отрезке $[400;2400]$ имеется $6$ суперсчастливых чисел: $549,1449,1539,1559,1649,2349.$

Ответ: 6 (это числа 549, 1449, 1539, 1559, 1649, 2349)

Ошибка.
Попробуйте повторить позже

Задача 16#129853Максимум баллов за задание: 7

Вася нарисовал на доске замкнутую кривую $ABCD,$ состоящую из четырех звеньев: $AB$ — дуга окружности, меньшая полуокружности, $BC$ — отрезок, $CD$ — дуга окружности, большая полуокружности, $DA$ — отрезок, таким образом, что любые два соседних звена перпендикулярны друг другу. Петя нарисовал кривую данного вида так, чтобы длины всех звеньев совпадали. Какие тогда будут углы у дуг $AB$ и $DC?$

Примечание: прямая перпендикулярна дуге окружности, если прямая перпендикулярна касательной к окружности.

Источники: Ломоносов - 2025, 10.8 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Пока не совсем понятно, как у нас может выглядеть картинка, попробуем порассуждать без неё... Что интересного нам может дать условие на перпендикулярность отрезка дуге окружности?

Подсказка 2

По условию это значит, что отрезок перпендикулярен касательной. А что ещё у окружности перпендикулярно касательной?

Подсказка 3

Правильно, радиус. Получается, радиус лежит на той же прямой, что и отрезок из условия. А можем ли мы сказать это про другой отрезок? Какой вывод из этого можно сделать?

Подсказка 4

Да, центр каждой из окружностей — это пересечение прямых, на которых лежат отрезки из условия. С этим знанием уже гораздо проще построить картинку, главное не забыть про все возможные конфигурации!

Подсказка 5

Нам не дано вообще никаких численных данных, а спрашивают, какими получатся угловые меры дуг. Может быть, мы сможем связать искомые дуги через угол, на который они опираются? Тогда, посчитав этот угол разными способами, мы получим для него уравнение, а если мы знаем угол, то недалеко и до градусной меры исходных дуг.

Подсказка 6

Как можно связать центральный угол окружности (выраженный в радианах) и длину дуги, на которую он опирается?

Подсказка 7

Произведение радиуса окружности на центральный угол будет длиной соответствующей дуги (вспомните, что такое 1 радиан по определению). Как тогда выразить угол каждой дуги через радиус и длину дуги?

Подсказка 8

Давайте введём длины дуг и радиусы окружностей и свяжем их между собой через длину отрезков из условия. Пусть обе дуги будут a, меньший радиус — r, тогда больший радиус — это R=r+a или R=2r+a в зависимости от картинки.

Подсказка 9

Выразим длины нужных нам дуг через введённые обозначения. Приравняйте величины углов и решите квадратное уравнение для r.

Показать ответ и решение

Так как прямая $BC$ перпендикулярна дуге $A⌣B,$ то радиус окружности, на которой лежит дуга, лежит на прямой $BC.$ Аналогично, на прямой $BC$ лежит радиус окружности, содержащей дугу $⌣ CD,$ а также радиусы обеих окружностей лежат на прямой $DA.$ Из-за того, что дуги не равны полуокружностям по условию, прямые $BC$ и $DA$ пересекаются. Из всего этого следует, что окружности имеют общий центр.

Также есть требование, что одна дуга больше полуокружности, а другая — меньше. С учётом того, что мы хотим получить равные длины всех звеньев ломаной, большая полуокружность должна быть у окружности меньшего радиуса, что оставляет нас с двумя вариантами ломаной.

Пусть