Ломоносов 2025
Ошибка.
Попробуйте повторить позже
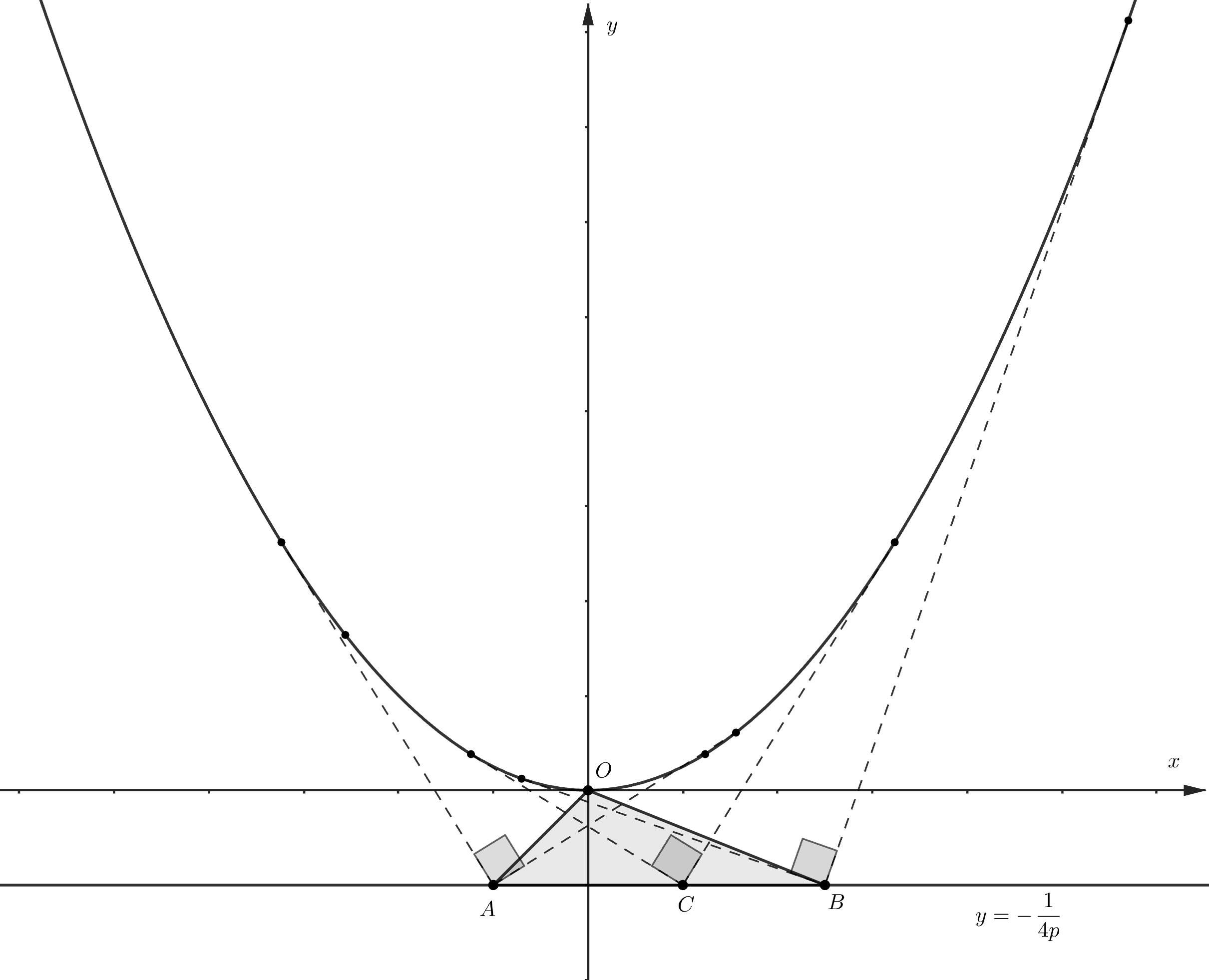
На чертеже есть парабола и три точки Из каждой точки к параболе проведены две перпендикулярные друг другу касательные.
Расстояние от вершины
параболы до прямой
равно 2. Найдите площадь треугольника
если
а
Источники:
Подсказка 1
Задачу приятно решать в координатах, но как их ввести, чтобы максимально упростить вычисления?
Подсказка 2
Конечно же, за начальную точку стоит взять вершину параболы — это позволит нам оставить только один коэффициент в её уравнении. Подумайте, как можно использовать условие о перпендикулярности касательных.
Подсказка 3
Если поработать с уравнениями касательных, можно понять, что они будут перпендикулярны лишь в том случае, если проведены из точек, лежащих на некоторой определённой прямой. А как нам помогают известные длины?
Подсказка 4
Неизвестный коэффициент найден благодаря расстоянию! Но однозначно ли взаимное расположение точек A, B и C? Осталось лишь воспользоваться формулой площади треугольника и получить ответ!
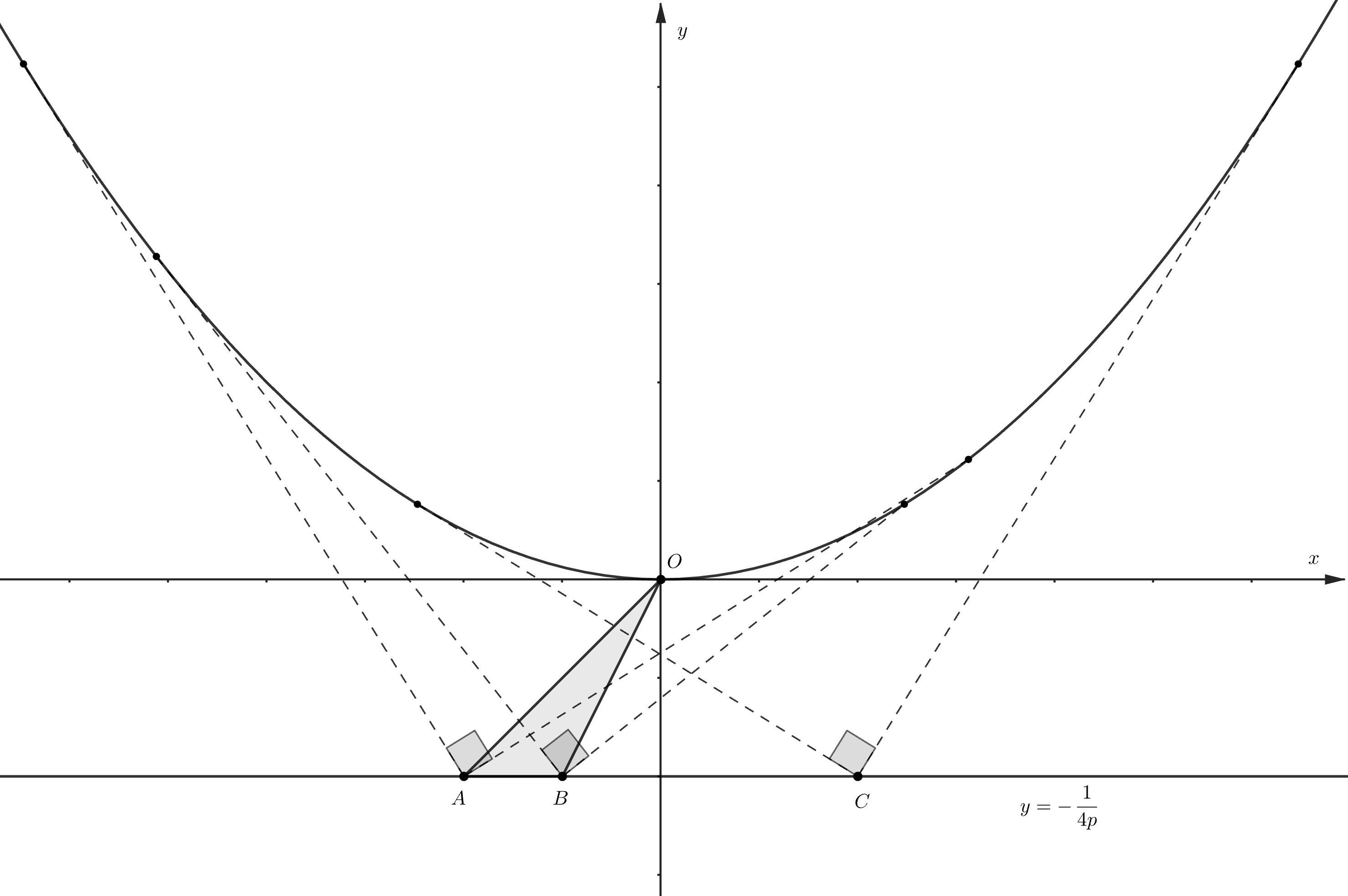
Пусть уравнение параболы Через точку
проходит прямая
Эта прямая будет касаться
параболы в том случае, если она не параллельна оси параболы (т.е.
) и имеет с параболой единственную общую точку — то есть
уравнение
должно иметь единственное решение относительно переменной
Уравнение квадратное — значит, для единственности решения нужно, чтобы дискриминант равнялся нулю.
Дискриминант этого уравнения равен
Он, в свою очередь, тоже образует квадратное уравнение, но для переменной
Угловые коэффициенты перпендикулярных прямых относятся так:
Значит, если из одной точки получилось
провести перпендикулярные касательные к параболе, то уравнение имеет такие корни
, что
а по теореме Виета это
значит, что
То есть и провести перпендикулярные касательные к параболе получится только из точек, лежащих на прямой
Точки
лежат на одной прямой, и расстояние до этой прямой от точки
известно из условия. Учитывая, что располагаться на
прямой
могут в разном порядке, мы получаем два возможных варианта ответа:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




