Открытая летняя олимпиада: продолжающие
Ошибка.
Попробуйте повторить позже
В Ромашковой Долине Крош с Ёжиком решили провести игру. На лужайке
появилась большая клетчатая доска размером клеток — почти как
шахматная, только ярче! Крош предложил друзьям придумать на ней загадочный
маршрут для поиска клада: в некоторых клетках он ярко нарисовал морковки,
чтобы обозначить “секретные точки”.
Известно, что в каждой строке и каждом столбце Крош обязательно
поставил хотя бы одну морковку. Ёжик заметил следующее: в каждой строке
находится нечётное число морковок, а в каждом столбце Крош нарисовал ровно
столько морковок, чтобы их число делилось на Какое минимальное и
максимальное количество клеток с морковками могло быть при таких
правилах?
В каждом столбце количество морковок кратно Значит, в каждом
столбце может быть либо
, либо
морковок. Всего морковок не меньше
Суммируя количество морковок по строкам, мы видим, что общее число
должно быть нечётным. Суммируя по столбцам, получаем, что оно делится на .
При этом в каждом столбце не более
морковок из
возможных. Значит, всего
нарисовано не больше, чем
морковки.
Единственное наибольшее нечётное число, кратное , не превосходящее
, —
это
. Следовательно, в таблице не больше
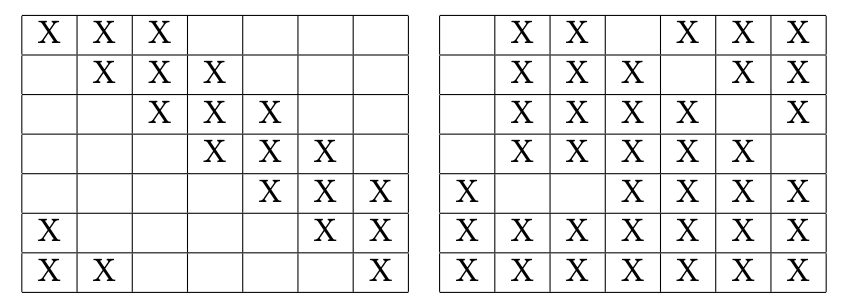
морковок. Примеры для каждого
случая на картинке ниже.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




