27.05 Кластеры в трехмерном пространстве

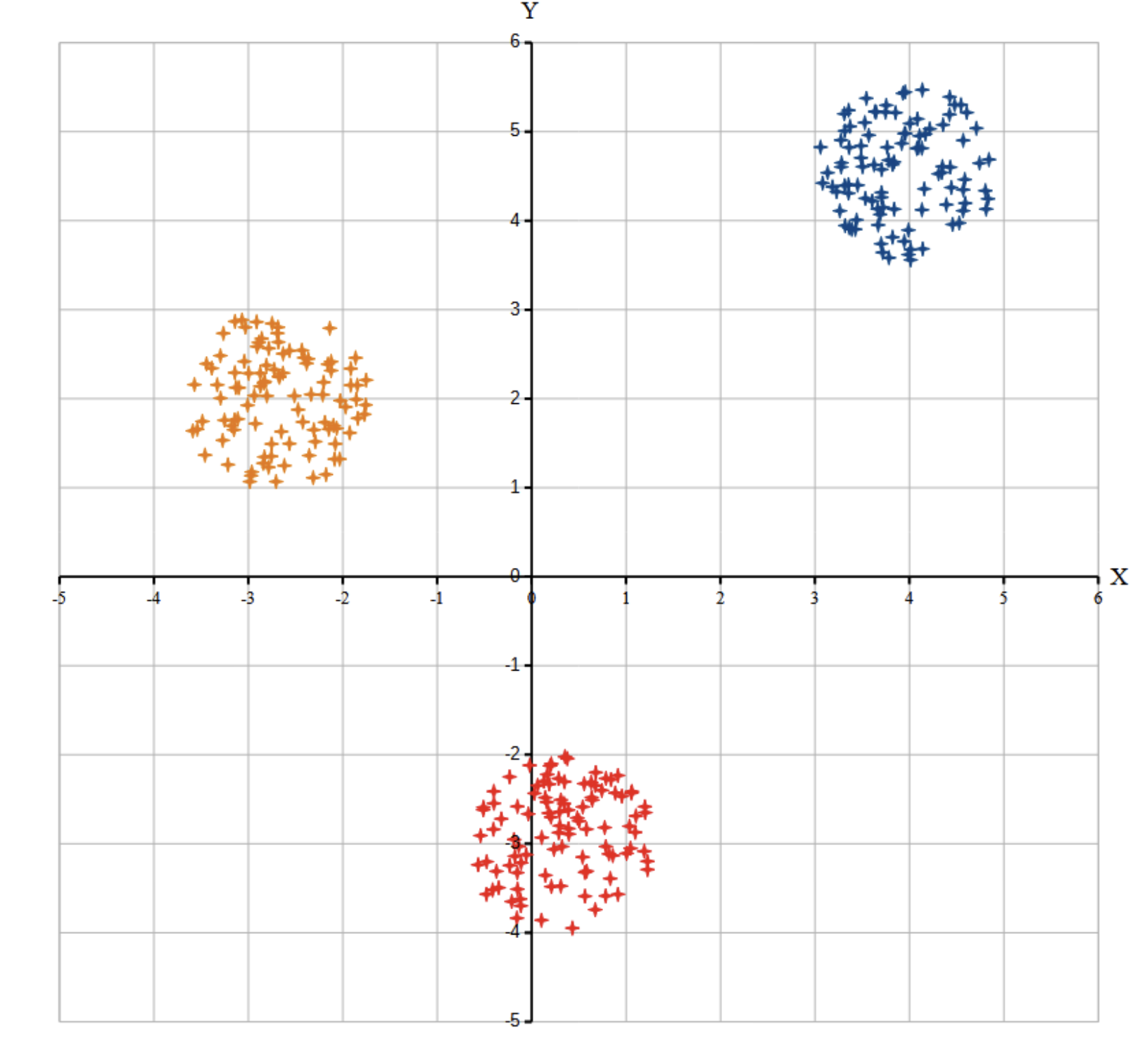
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в , перейдем в раздел «Вставка Диаграммы Точечная». Таким способом можно построим по отдельности двухмерные проекции кластеров на оси , и .

Диаграммы для файла А имеют вид:

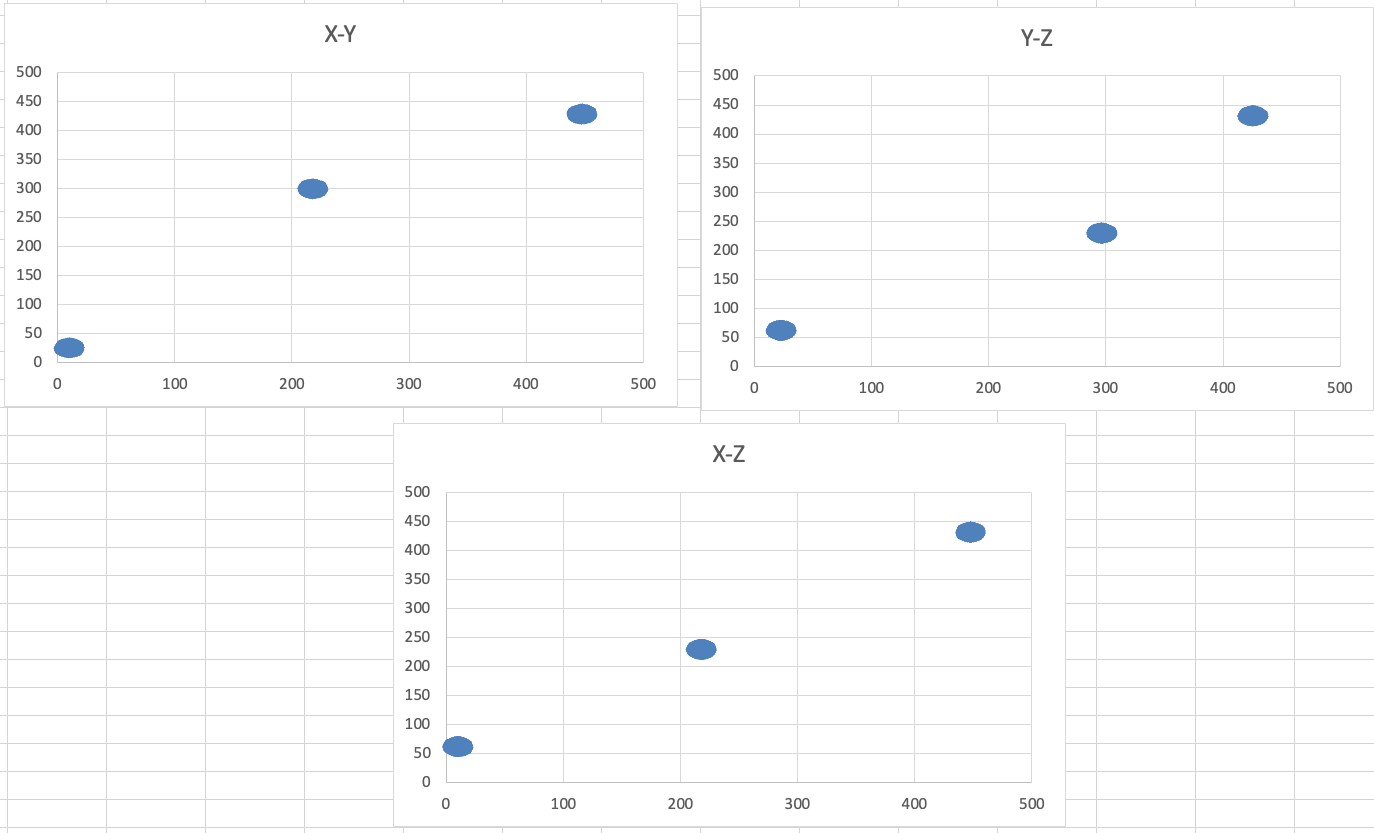
Из графика видно, что один кластер имеет абсциссы, меньшие 50, другой – от 200 до 250, а третий все остальные. Пользуясь этим знанием, разделим данные на кластеры в программе.

Код для файла А

from math import *
f = open(’4_A.txt’)
n = f.readline()

clusters = [[] for i in range(3)]
for i in f:
    star = list(map(float, i.replace(’,’, ’.’).split()))
    if star[0] < 50:
        clusters[0].append(star)
    elif 200 < star[0] < 250:
        clusters[1].append(star)
    else:
        clusters[2].append(star)
sum_x = sum_y = sum_z = tx = ty = tz = 0
for cluster in clusters:
    mn = 10**20
    for star_1 in cluster:
        sm = 0
        for star_2 in cluster:
            sm += dist(star_1,star_2)
        if sm < mn:
            mn = sm
            tx,ty,tz = star_1
    sum_x += tx
    sum_y += ty
    sum_z += tz

print(int(((sum_x/3)*(sum_y/3)*(sum_z/3))/25))

Диаграммы для файла Б имеют вид:

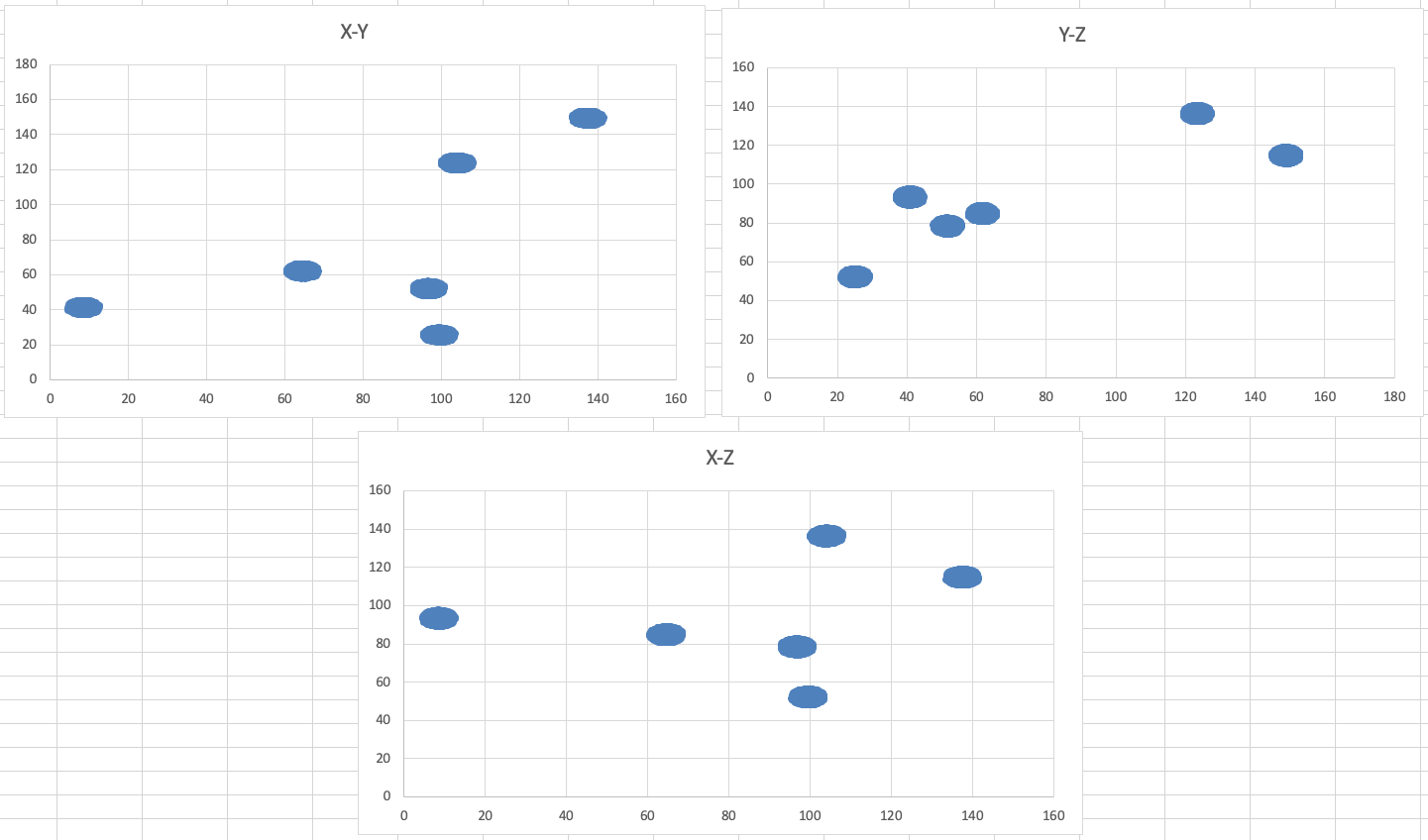
Из графика видно, что шесть кластеров распределены следующим образом:

1. Первый имеет абсциссы меньшие 20

2. Второй абсциссы от 50 до 80

3. Третий ординаты меньшие 40 и абсциссы от 90 до 110

4. Четвертый ординаты от 40 до 60 и абсциссы от 80 до 120

5. Пятый абсциссы меньшие 120, а ординаты большие 100

6. Шестой все остальные точки

Код для файла Б

from math import *
f = open(’4_B.txt’)
n = f.readline()

clusters = [[] for i in range(6)]
for i in f:
    star = list(map(float, i.replace(’,’, ’.’).split()))
    if star[0] < 20:
        clusters[0].append(star)
    elif 50 < star[0] < 80:
        clusters[1].append(star)
    elif 90 < star[0] < 110 and star[1] < 40:
        clusters[2].append(star)
    elif 80 < star[0] < 120 and 40 < star[1] < 60:
        clusters[3].append(star)
    elif star[0] < 120 and star[1] > 100:
        clusters[4].append(star)
    else:
        clusters[5].append(star)

sum_x = sum_y = sum_z = tx = ty = tz = 0
for cluster in clusters:
    mn = 10**20
    for star_1 in cluster:
        sm = 0
        for star_2 in cluster:
            sm += dist(star_1,star_2)
        if sm < mn:
            mn = sm
            tx,ty,tz = star_1
    sum_x += tx
    sum_y += ty
    sum_z += tz
print(int((sum_x/6) * (sum_y/6) * (sum_z/6) / 75))