27.05 Кластеры в трехмерном пространстве
Ошибка.
Попробуйте повторить позже
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба.
Кластер звёзд – это набор звёзд (точек) на графике, каждая из которых находится от хотя бы одной другой звезды на
расстоянии не более условных единиц. Каждая звезда обязательно принадлежит только одному из
кластеров.
Истинный центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна.
Под расстоянием понимается расстояние Евклида между двумя точками и
в трехмерном
пространстве, которое вычисляется по формуле:
Аномалиями назовём точки, находящиеся на расстоянии более от точек кластеров. При расчётах аномалии
учитывать не нужно.
В файле A хранятся данные о звёздах двух кластеров, где для каждого кластера. В каждой строке
записана информация о расположении на карте одной звезды: сначала координата
, затем координата
, затем
координата
. Значения даны в условных единицах, которые представлены вещественными числами. Известно, что
количество звёзд не превышает 10000.
В файле Б хранятся данные о звёздах четырех кластеров, где для каждого кластера. Известно, что
количество звёзд не превышает 21000. Структура хранения информации о звездах в файле Б аналогична файлу
А.
Для каждого файла определите координаты центроида каждого кластера, затем вычислите три числа: –
среднее арифметическое абсцисс центроидов кластеров,
– среднее арифметическое ординат центроидов кластеров
и
– среднее арифметическое аппликат центроидов кластеров.
В ответе запишите шесть чисел через пробел: сначала целую часть произведений ,
и
для файла А, далее целую часть произведения
,
и
для файла
Б.
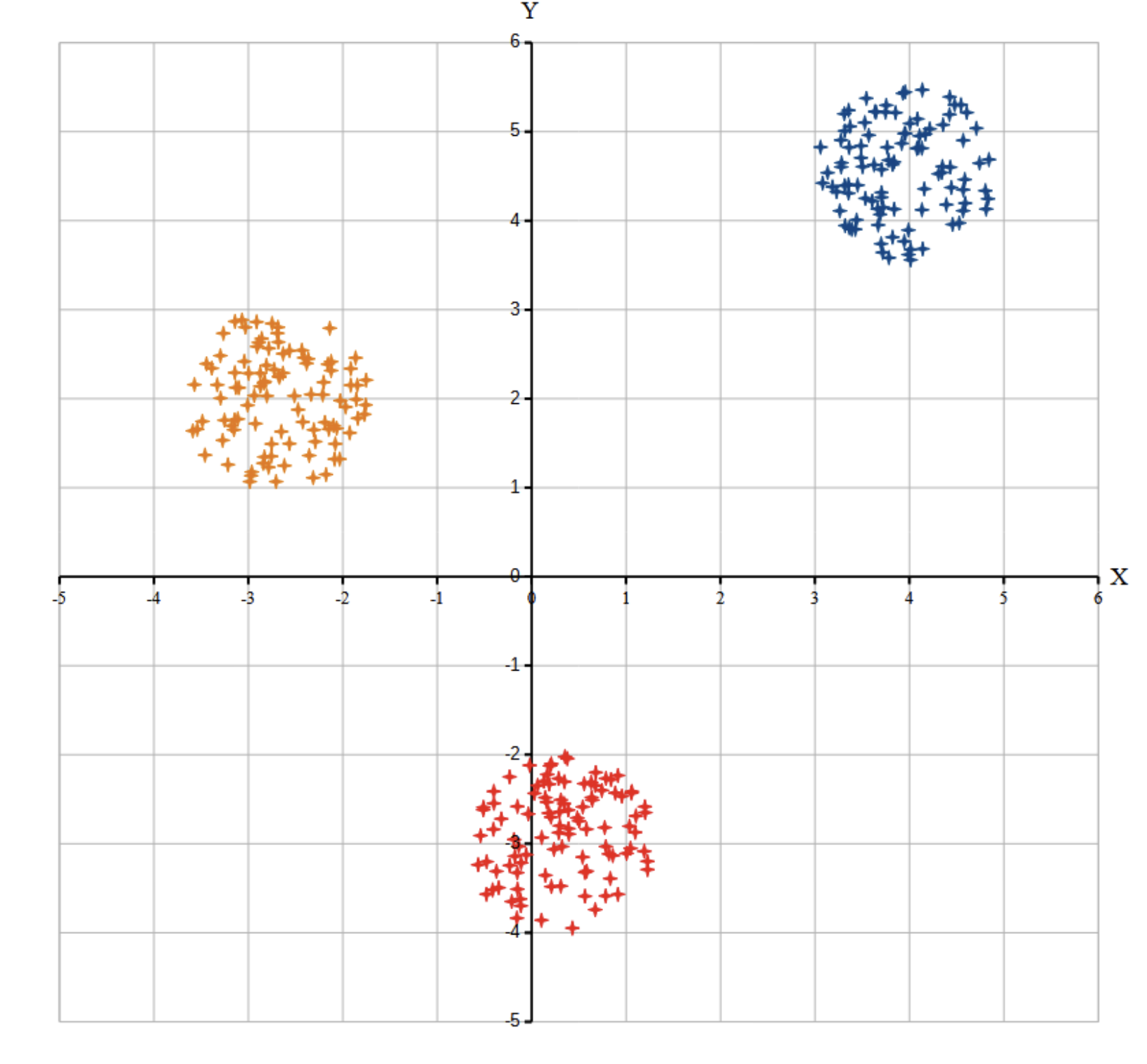
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в ,
перейдем в раздел «Вставка
Диаграммы
Точечная». Таким способом можно построить только
двухмерную проекцию кластеров на ось
, однако для примерного понимания положения кластеров в
пространстве этой диаграммы будет достаточно.
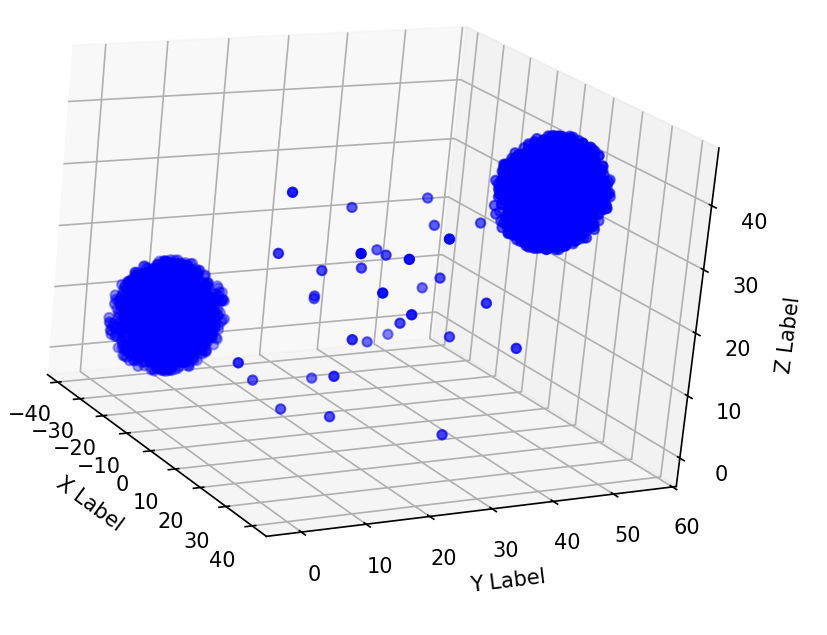
Дополнительно для визуализации можно сделать 3Д график, но это требует более углубленных навыков владения Python и его библиотек.
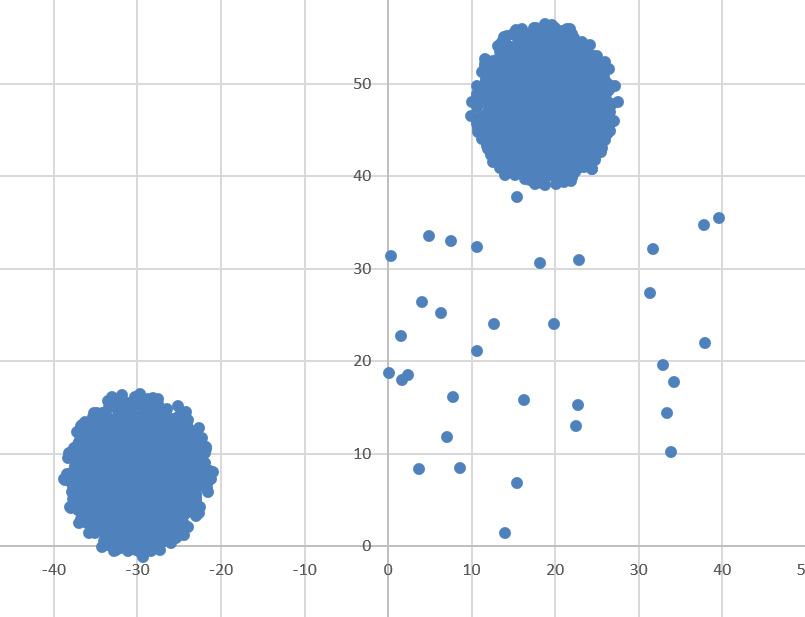
Диаграммы для файла А имеет вид:
Код для файла А
from math import *
def dist_3d(p1, p2): # Расстояние между точками в декартовой системе координат
return ((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2 + (p1[2] - p2[2])**2) ** 0.5
def dbscan(a, r):
cl = [] # Инициализируем список для хранения кластеров
while a: # Пока есть элементы в входном массиве ’a’
cl.append([a.pop(0)])
for i in cl[-1]: # Проходим по элементам последнего кластера
for j in a[:]:
if dist_3d(i, j) <= r:
cl[-1].append(j) # Добавляем ’j’ в текущий кластер
a.remove(j) # Удаляем ’j’ из списка ’a’, чтобы не проверять его снова
return cl
f = open("5_A.txt")
s = f.readline()
a = [list(map(float, i.replace(",", ".").split())) for i in f]
cl = dbscan(a, 2) # Для файла A
cl_total = []
for i in cl:
if len(i) > 10: cl_total.append(i)
sum_x = sum_y = sum_z = 0
for cluster in cl_total:
tx = ty = tz = 0
mn = 10 ** 20
for centroid in cluster:
sm = 0
for star in cluster:
sm += dist_3d(centroid, star)
if sm < mn:
mn = sm
tx, ty , tz = centroid[0], centroid[1], centroid[2]
sum_x += tx
sum_y += ty
sum_z += tz
print(int(abs(sum_x/ 2) * 100), int(abs(sum_y/ 2) * 100), int(abs(sum_z/ 2) * 100))
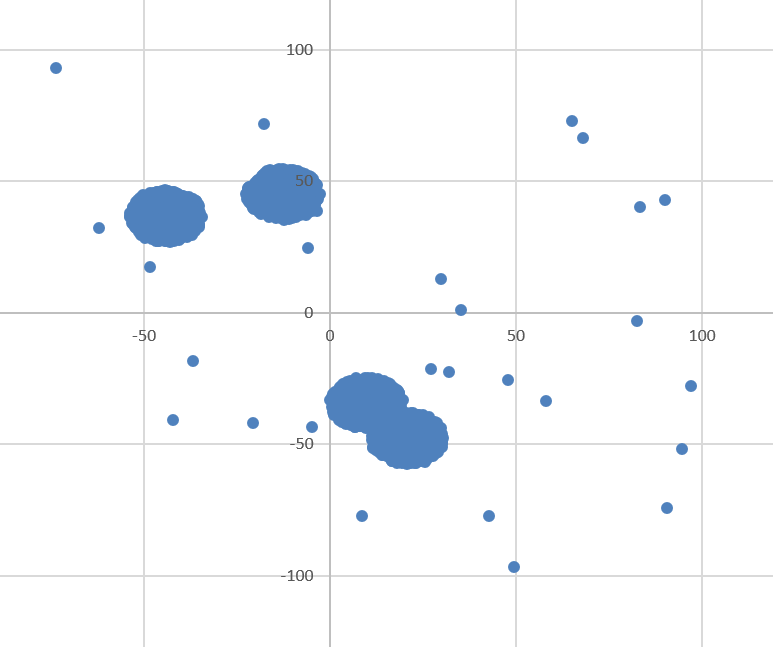
Диаграмма для файла Б имеет вид:
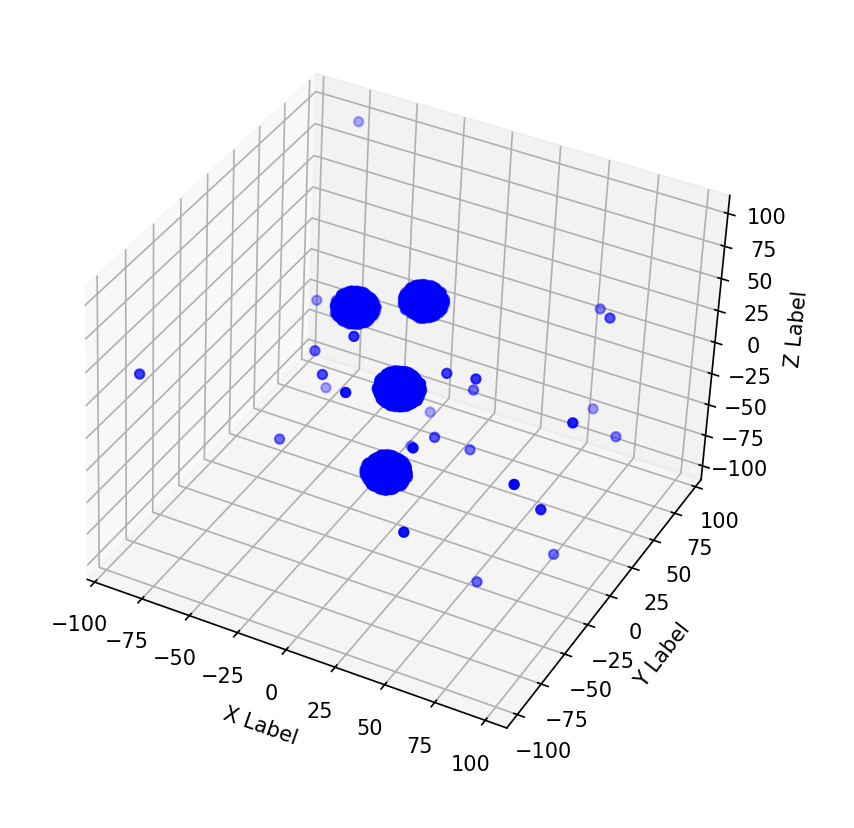
Код для файла Б
from math import *
def dist_3d(p1, p2): # Расстояние между точками в декартовой системе координат
return ((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2 + (p1[2] - p2[2])**2) ** 0.5
def dbscan(a, r):
cl = [] # Инициализируем список для хранения кластеров
while a: # Пока есть элементы в входном массиве ’a’
cl.append([a.pop(0)])
for i in cl[-1]: # Проходим по элементам последнего кластера
for j in a[:]:
if dist_3d(i, j) <= r:
cl[-1].append(j) # Добавляем ’j’ в текущий кластер
a.remove(j) # Удаляем ’j’ из списка ’a’, чтобы не проверять его снова
return cl
f = open("5_B.txt")
s = f.readline()
a = [list(map(float, i.replace(",", ".").split())) for i in f]
cl = dbscan(a, 3) # Для файла Б
cl_total = []
for i in cl:
if len(i) > 10: cl_total.append(i)
sum_x = sum_y = sum_z = 0
for cluster in cl_total:
tx = ty = tz = 0
mn = 10 ** 20
for centroid in cluster:
sm = 0
for star in cluster:
sm += dist_3d(centroid, star)
if sm < mn:
mn = sm
tx, ty , tz = centroid[0], centroid[1], centroid[2]
sum_x += tx
sum_y += ty
sum_z += tz
print(int(abs(sum_x/ 4) * 100), int(abs(sum_y/ 4) * 100), int(abs(sum_z/ 4) * 100))
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





