Тема Закл (финал) 9 класс

Закл 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 9 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#129164Максимум баллов за задание: 7

Петя и Вася знают лишь натуральные числа, не превосходящие $109 − 4000.$ Петя считает хорошими числа, представимые в виде

abc +ab+ ac+bc,

где $a,b$ и $c$ — натуральные числа, не меньшие 100. Вася считает хорошими числа, представимые в виде

xyz − x − y− z,

где $x,y$ и $z$ — натуральные числа, большие 100. Для кого из них хороших чисел больше?

Источники: ВСОШ, ЗЭ, 2024, 9.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Чтобы сравнить количества чисел, можно построить какое-то соответствие. Например, каждому числу одного человека сопоставить какое-то число другого человека.

Подсказка 2:

Попробуйте сопоставить числу Пети какое-то число Васи. А потом найдите какое-нибудь число Васи, которому не сопоставлено число Пети.

Подсказка 3:

Пусть k — число Пети. Что можно сказать про число k − 2?

Подсказка 4:

Пусть k = abc + ab + ac + bc, тогда k − 2 = (a + 1)(b + 1)(c + 1) − (a + 1) − (b + 1) − (c + 1).

Показать ответ и решение

Если число

9 k= abc+ ab+ ac+ bc≤ 10 − 4000

хорошее для Пети, то число

k− 2= (a+1)(b+1)(c+ 1)− (a+ 1)− (b+ 1)− (c+1)

является хорошим для Васи. Значит, если для Пети есть $p$ хороших чисел, то мы предъявили $p$ различных чисел, хороших для Васи, и все они строго меньше, чем $109− 4000.$ Но число

109− 4000 =(1000 − 1)⋅1000⋅(1000 +1)− (1000− 1)− 1000− (1000+ 1)

также является хорошим для Васи; поэтому для Васи есть хотя бы $p+1$ хорошее число.

Ответ:

для Васи

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#129170Максимум баллов за задание: 7

У натурального числа ровно 50 делителей. Может ли оказаться, что никакая разность двух различных его делителей не делится на 100?

Источники: ВСОШ, ЗЭ, 2024, 9.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Ясно, что нужно смотреть на последние две цифры всех чисел. Если у каких-то двух они совпадают, то их разность будет делиться на 100.

Подсказка 2:

Давайте назовём последние две цифры числа "хвостом". Заметим, что хвост числа n даёт такие же остатки при делении на некоторые числа, что и само n.

Подсказка 3:

Если число делится на 5, может ли оно обладать таким свойством? Сколько у него будет делителей, кратных 5? А сколько всего существует "хвостов", кратных 5?

Подсказка 4:

Покажите, что у числа хотя бы половина делителей будет делиться на 5. Попробуйте аналогично разобрать случаи, когда n нечётно и когда n кратно 2, но не 4.

Подсказка 5:

Итак, кажется, вы пришли к тому, что такое число не делится на 5 и делится на 2 хотя бы во второй степени. Попробуйте обозначить через r степень вхождения 2 в n и поработать с ней.

Подсказка 6:

Докажите, что количество делителей кратно r + 1. Для этого достаточно разбить делители некоторым образом на цепочки по r + 1 делителю в каждой.

Подсказка 7:

Используя всю информацию, попробуйте оценить количество нечётных делителей, делителей, кратных 2, но не 4, и кратных 4.

Показать ответ и решение

Предположим, что такое число $n$ существует. Условие равносильно тому, что все числа, образованные последними двумя цифрами делителей, различны (мы считаем, что к однозначным числам спереди приписаны нули). Назовём такую пару последних цифр хвостом числа. Заметим, что хвост числа имеет те же остатки от деления на $4$ и на $5,$ что и исходное число.

Предположим, что $n$ делится на 5. Тогда для любого его делителя $d,$ не кратного $5,$ существует и делитель $5d,$ кратный $5.$ При этом для разных делителей $d$ мы получаем разные делители $5d;$ поэтому количество кратных $5$ делителей не меньше половины, то есть не меньше $25.$ Но такие делители имеют хвосты, оканчивающиеся либо на $0,$ либо на $5.$ Таких возможных хвостов не больше $20,$ поэтому два из них совпадают. Это противоречие показывает, что $n$ не делится на $5,$ и хвосты его делителей не могут оканчиваться на $0$ или $5.$

Если число $n$ нечётно, то все его делители также нечётны. Однако существует всего $50$ возможных нечётных хвостов, и $10$ из них оканчиваются на $5,$ то есть не могут появиться. Поэтому и в этом случае найдутся два одинаковых хвоста.

Если число $n$ делится на $2,$ но не на $4,$ то все его делители разбиваются на пары $(d,2d),$ где $d$ — нечётный делитель $n.$ При этом все числа вида $2d$ имеют хвосты, не делящиеся на $4,$ а таких хвостов (при этом не делящихся на $5$ ) всего $20.$ Значит, два из этих хвостов одинаковы.

Наконец, пусть наибольшая степень двойки, на которую делится $n,$ равна $2r,$ где $r≥ 2.$ Тогда, если $d$ — нечётный делитель $n,$ то числа $d,$ $2d,$ $22d,$ …, $2rd$ также будут делителями $n,$ и этим исчерпываются все делители $n.$ Поэтому общее число делителей $n$ будет кратно $r+1.$ Таким образом, $50$ делится на $r+ 1$ и, значит, $r ≥4.$

Тогда $n$ имеет

-50-≤ 10 r+ 1

нечётных делителей и столько же делителей, которые чётны и не делятся на четыре. Стало быть, оставшиеся делители (которых не меньше $30$ ) кратны $4$ и, значит, их хвосты также кратны четырём. Но таких хвостов возможно лишь $20,$ поэтому опять два из них совпадут.

Ответ:

нет

Ошибка.
Попробуйте повторить позже

Задача 3#129173Максимум баллов за задание: 7

Двум мальчикам выдали по мешку картошки, в каждом мешке по 150 клубней. Ребята по очереди перекладывают картошку, каждый своим очередным ходом перекладывает ненулевое количество клубней из своего мешка в чужой. При этом они должны соблюдать условие новой возможности: на каждом ходе мальчик должен переложить больше клубней, чем у него было в мешке перед любым из его предыдущих ходов (если такие ходы были). Так, первым своим ходом мальчик может переложить любое ненулевое количество, а своим пятым ходом мальчик может переложить 200 клубней, если перед его первым, вторым, третьим и четвёртым ходами количества клубней в его мешке были меньше 200. Какое максимальное суммарное количество ходов могут совершить ребята?

Источники: ВСОШ, ЗЭ, 2024, 9.3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1.

Чтобы следить за процессом, надо ввести обозначения. Пусть aₙ — количество клубней у мальчика, сделавшего n-ый ход, сразу после хода. Попробуйте вывести какие-то условия на полученную последовательность.

Показать ответ и решение

Пусть в процессе было $N$ ходов.

Рассмотрим $k$ -й ход. Обозначим через $ak$ количество клубней у мальчика, делавшего этот ход, сразу после хода. Тогда у другого мальчика после хода $300− ak$ клубней. Также обозначим через

a0 = 150= 300− a0

количество клубней у (любого) мальчика перед первым ходом.

В этих обозначениях, перед $k$ -м ходом у мальчика, делавшего его, было $300− a k−1$ клубней, а после него — $a k$ клубней. Значит, на этом ходу он передавал $300− a − a k−1 k$ клубней. Если $k≥ 3,$ то это количество должно быть больше, чем количество клубней у этого мальчика перед его предыдущим ( $(k− 2)$ -м) ходом, то есть не меньше, чем $300− a . k−3$ Итак,

300− ak−1− ak >300− ak−3 ⇐ ⇒ ak−3 > ak−1 +ak.

Поскольку все числа $ai$ целые, получаем, что

ak−3 ≥ak−1+ ak+1

при всех $k =3,4,$ $...,N.$

Теперь можно получить оценки на числа $ai,$ действуя «с конца». Определим числа $b0,b1,$ $b2,...,$ условиями

b =b = b = 0; b = b + b+ 1. 0 1 2 k+3 k+1 k

Докажем, что $aN −k ≥ bk$ и $bk+1 ≥bk,$ индукцией по $k= 0,1,...,N.$ При $k =0,$ $1,2$ неравенства очевидны; для перехода, чтобы доказать неравенство при некотором $k ≥3,$ достаточно заметить, что

aN−k ≥aN −k+2 +aN−k+3+ 1≥ bk− 2+bk−3+ 1= bk,

bk+1 = bk−1+ bk− 2+1 ≥bk−2+ bk−3+ 1= bk.

Итак, мы получаем, что $a0 ≥ bN.$ Приведём таблицу первых значений чисел $bk :$


$k$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20

$bk$	0	0	0	1	1	2	3	4	6	8	11	15	20	27	36	48	64	85	113	150	199

Значит, из условия $b ≤150 N$ получаем, что $N ≤19.$

Пример, когда дети могут сделать $19$ ходов, следует из построения выше. Изначально у каждого ребёнка по $b =150 19$ клубней. Пусть дети действуют так, чтобы после $k$ -го (с начала) хода у перекладывавшего оставалось ровно $b 19−k$ клубней; тогда на $k$ -м (с начала) ходе ребёнок перекладывает

300− b20−k− b19−k

клубней, а перед любым предыдущим его ходом у него будет $300− b i$ клубней при $i≥17− k,$ причём

300 − bi ≤ 300− b17−k < 300− b19−k− b20−k.

Значит, этот ход удовлетворяет условию, и дети могут сделать 19 таких ходов.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 4#129175Максимум баллов за задание: 7

Дан вписанный четырёхугольник $ABCD,$ в котором $∠A+ ∠D = 90∘.$ Его диагонали пересекаются в точке $E.$ Прямая $ℓ$ пересекает отрезки $AB,$ $CD,$ $AE$ и $ED$ в точках $X,$ $Y,$ $Z$ и $T$ соответственно. Известно, что $AZ =CE$ и $BE = DT.$ Докажите, что длина отрезка $XY$ равна диаметру окружности, описанной около треугольника $ETZ.$

Источники: ВСОШ, ЗЭ, 2024, 9.4 (см. olympiads.mccme.ru)

Показать доказательство

Применяя теорему Менелая к треугольнику $ETZ$ и секущим $AXB$ и $CY D,$ получаем

AZ- BE- XT- CE- DT- YZ- AE ⋅BT ⋅XZ = CZ ⋅DE ⋅ YT =1.

Из равенств $AZ = CE$ и $BE = DT$ следует, что $AE = CZ$ и $BT = DE.$ Подставляя все эти равенства, получаем, что

XT YZ XZ- = YT;

это означает, что точки $X$ и $Y$ симметричны относительно середины $S$ отрезка $ZT$ (см. рис.).

Из условия следует, что лучи $AB$ и $DC$ пересекаются в некоторой точке $F$ под прямым углом. Тогда в прямоугольном треугольнике $XF Y$ медиана $FS$ равна половине гипотенузы $XY.$

Обозначим через $M$ и $N$ середины $AD$ и $BC$ соответственно, а через $O$ — центр окружности $(ABCD ).$ Тогда $O$ — точка пересечения серединных перпендикуляров к $AC$ и $BD,$ которые совпадают с серединными перпендикулярами к $EZ$ и $ET$ соответственно. Значит, $O$ — также центр окружности $(ET Z),$ а $OE$ — её радиус. Поэтому нам достаточно доказать, что $OE = FS.$ Мы докажем, что $OEF S$ — параллелограмм, откуда это и следует.

Поскольку $EN$ — медиана в треугольнике $EBC,$ а $MS$ — отрезок, соединяющий середины противоположных сторон четырёхугольника $AZT D,$ имеем

$PIC$

−−→ −−→ −−→ −→ −−E→N = EB-+EC--= DT +-AZ-= −M−→S. 2 2

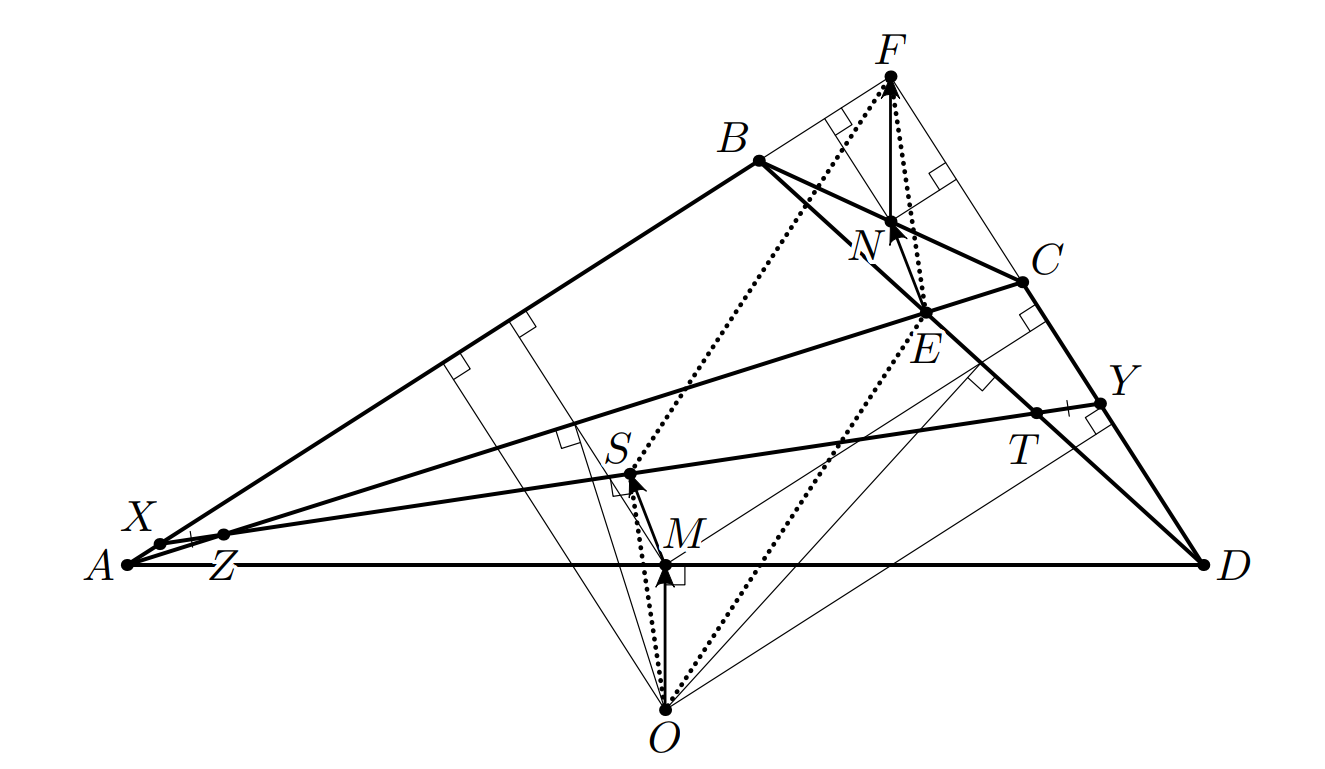
В прямоугольном треугольнике $FBC$ проекции вектора медианы $−N−→F$ на прямые $BF$ и $CF$ равны $−−B→F∕2$ и $−C→F ∕2$ соответственно. Поскольку $O$ и $M$ — центры окружностей $(ABCD )$ и $(ADF )$ соответственно, при проекции на те же прямые первая попадает в середины отрезков $AB$ и $CD,$ а вторая — в середины $AF$ и $DF.$ Поэтому проекции вектора

−−→ −−→ −→ −−→ −−→ OM = AM − AO =− DM − DO

на эти прямые равны

−→ −→ −−→ −−→ −−→ −→ AP −-AB-= BF-, DF-−DO-= CF-. 2 2 2 2

Значит, проекции векторов $−N−→F$ и $−O−→M$ на наши две прямые соответственно равны, откуда $−N−→F =−O−M→.$

Итак,

−O→S = −−O→M +−M−S→ =−N−F→+ −E−→N = −−E→F,

откуда и следует, что $OEF S$ — параллелограмм.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Есть и другие доказательства того, что $OEF S$ — параллелограмм. Например, можно использовать тот факт, что точки $O$ и $F$ изогонально сопряжены относительно треугольника $ADE.$

Ошибка.
Попробуйте повторить позже

Задача 5#129177Максимум баллов за задание: 7

Квартал представляет собой клетчатый квадрат $10× 10.$ В новогоднюю ночь внезапно впервые пошёл снег, и с тех пор каждую ночь на каждую клетку выпадало ровно по 10 см снега; снег падал только по ночам. Каждое утро дворник выбирает один ряд (строку или столбец) и сгребает весь снег оттуда на один из соседних рядов (с каждой клетки — на соседнюю по стороне). Например, он может выбрать седьмой столбец и из каждой его клетки сгрести снег в клетку слева от неё. Сгребать снег за пределы квартала нельзя. Вечером сотого дня года в город приедет инспектор и найдёт клетку, на которой лежит сугроб наибольшей высоты. Цель дворника — добиться, чтобы эта высота была минимальна. Сугроб какой высоты найдёт инспектор?

Источники: ВСОШ, ЗЭ, 2024, 9.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1.

Хочется верить, что в оптимальном примере во всех непустых ячейках почти поровну снега.

Показать ответ и решение

Будем измерять высоту сугроба в дециметрах. Также будем считать, что сторона одной клетки равна $1$ дм, то есть за каждую ночь на клетку выпадает $1$ $3 дм$ снега.

Докажем, что после сотого утра найдется сугроб высотой не менее $112$ дм. Предположим, что такого сугроба нет. Так как дворник в сотое утро полностью сгреб снег с какого-то ряда, в десяти клетках квадрата снега нет. В каждой из оставшихся $90$ клеток, по нашему предположению, не более $111$ $3 дм$ снега, то есть всего снега не больше, чем $9990$ $3 дм .$ Однако за $100$ ночей суммарно выпало $10000$ $3 дм$ снега. Противоречие.

Покажем, как может действовать дворник, чтобы после сотого утра каждый сугроб имел высоту не более $112$ дм, то есть в каждой клетке было не более $112$ $3 дм$ снега.

Способ 1. Первые $11$ дней дворник сгребает снег из второго столбца в первый, следующие $11$ дней дворник сгребает снег из третьего столбца во второй, затем $11$ дней из четвёртого в третий, и т. д. Через $99$ дней в десятом столбце не будет снега. Посчитаем, сколько снега стало в столбце $i≤ 9$ через $99$ дней. Вечером $11(i− 1)$ -го дня в столбце номер $i$ не было снега, а в столбце $i+ 1$ в каждой клетке было по $11(i− 1)$ $дм3$ снега. На следующий вечер в столбце $i$ станет по $11(i− 1)+ 2$ $дм3$ снега в каждой клетке. Затем ещё десять дней количество снега в каждой клетке $i$ -го столбца будет увеличиваться на $2,$ а затем $11(9− i)$ дней — на $1.$ Итого, через $99$ дней в каждой клетке столбца $i$ будет по

11(i− 1)+22+ 11(9− i) =110 дм3 снега.

В сотую ночь выпадет ещё по $1$ $дм3$ в каждую клетку. А сотым утром дворник сгребёт снег из десятого столбца в девятый. Таким образом, в каждой клетке будет не более $112$ $дм3$ снега.

_________________________________________________________________________________________________________________________________________________________________________________

Способ 2. Пусть дворник сгребёт снег из $2$ -го столбца в $1$ -ый, из $3$ -го во $2$ -й, …, из $10$ -го в $9$ -ый. Тогда вечером девятого дня в первых девяти столбцах будет по $10$ дм $3$ снега в каждой клетке, а в десятом столбце снега не будем. Затем дворник проделывает аналогичный процесс в обратном порядке: из $9$ -го в $10$ -ый, из $8$ -го в $9$ -ый, …, из $2$ -го в первой. Тогда вечером $18$ -го дня в клетках последних девяти столбцов будет по $20$ $дм3$ снега, а в первом столбце не будет снега. Аналогично повторим такие сдвиги (каждый длится $9$ дней) ещё $9$ раз (всего $11$ сдвигов), и через $99$ дней получим в клетках девяти столбцов по $110$ $дм3$ снега и один крайний столбец пустой. Сотым утром сгребаем снег из этого крайнего в соседний и получаем не более $112$ $дм3$ снега в каждой клетке.

Ответ:

1120 см

Ошибка.
Попробуйте повторить позже

Задача 6#129178Максимум баллов за задание: 7

Высоты остроугольного треугольника $ABC,$ в котором $AB <AC,$ пересекаются в точке $H,$ а $O$ — центр описанной около него окружности $Ω.$ Отрезок $OH$ пересекает описанную около треугольника $BHC$ окружность в точке $X,$ отличной от $O$ и $H.$ Окружность, описанная около треугольника $AOX,$ пересекает меньшую дугу $AB$ окружности $Ω$ в точке $Y.$ Докажите, что прямая $XY$ делит отрезок $BC$ пополам.

Источники: ВСОШ, ЗЭ, 2024, 9.6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Как ортоцентр треугольника связан с серединой одной из сторон? При чём здесь центр описанной окружности?

Показать доказательство

Пусть $H ′$ и $X ′$ — точки, симметричные точкам $H$ и $X$ относительно середины стороны $BC$ соответственно (см. рис.). Тогда $′ ′ HXH X$ — параллелограмм. Так как

′ ∘ ∠BX C = ∠BHC = ∠BHC =180 − ∠BAC,

точки $X ′$ и $H ′$ лежат на окружности $Ω.$

$PIC$

При этом, поскольку $H′B ∥ CH ⊥AB,$ точка $H′$ диаметрально противоположна точке $A$ на этой окружности; следовательно, $AH ′$ проходит через $O.$ Вспоминая, что

XO ∥ H′X ′,

получаем

∠AYX ′ = 180∘− ∠AH ′X ′ =180∘− ∠AOX = ∠AYX,

это и означает, что точки $Y,X$ и $′ X$ лежат на одной прямой, делящей $BC$ пополам.

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#129179Максимум баллов за задание: 7

На доске написаны 8 различных квадратных трёхчленов; среди них нет двух, дающих в сумме нулевой многочлен. Оказалось, что если выбрать любые два трёхчлена $g1(x),g2(x)$ с доски, то оставшиеся 6 трёхчленов можно обозначить как $g3(x),$ $g4(x),$ …, $g8(x)$ так, что у всех четырех многочленов $g1(x)+ g2(x),$ $g3(x)+ g4(x),$ $g5(x)+ g6(x)$ и $g7(x)+g8(x)$ есть общий корень. Обязательно ли все трёхчлены на доске имеют общий корень?

Источники: ВСОШ, ЗЭ, 2024, 9.7 (см. olympiads.mccme.ru)

Показать ответ и решение

Построим пример 8 квадратных трёхчленов, удовлетворяющих условию задачи:

2 2 2 f1(x)= −x + 2; f2(x)= 3x − 2; f3(x)= −4x +3;

2 2 2 f4(x)=2x − 3; f5(x)= −4x + x+ 4; f6(x)= 4x +x− 4;

f (x) =− 5x2− x+ 5; f (x)= 5x2− x − 5. 7 8

Данные многочлены составлены так, чтобы их значения в точках $x =− 1,0,1$ соответствовали следующей таблице:


$x$	$f1(x)$	$f2(x)$	$f3(x)$	$f4(x)$	$f5(x)$	$f6(x)$	$f7(x)$	$f8(x)$

$−1$	1	1	$−1$	$−1$	$−1$	$−1$	1	1

0	2	$−2$	3	$−3$	4	$−4$	5	$− 5$

1	1	1	$−1$	$−1$	1	1	$−1$	$− 1$

У трёхчленов этого примера нет общего корня, его нет даже у $f1(x)$ и $f2(x).$ Осталось показать, что они удовлетворяют условию. Очевидно, никакие два из этих трёхчленов не дают в сумме ноль.

Пусть выбрана какая-то пара из этих квадратных трёхчленов. Если была выбрана пара $(f2k−1(x),f2k(x)),$ где $k= 1,$ $2,3,4,$ то все многочлены можно разбить на пары $(f1(x),f2(x));$ $(f3(x),f4(x));$ $(f5(x),f6(x));$ $(f7(x),f8(x)),$ каждая сумма этих пар имеет корень $0.$

В противном случае нетрудно убедиться, что значение суммы двух выбранных трёхчленов или в точке $x0 = −1,$ или в точке $x0 =1$ (а может быть, и в обеих сразу) равняется нулю. Выберем такое $x0.$ Оставшиеся многочлены в точке $x0$ принимают значения $−1$ и $1$ ровно по три раза, и их можно разбить на пары так, чтобы в $x0$ суммы всех четырёх пар равнялись нулю, то есть $x0$ было их общим корнем.

Ответ:

нет, не обязательно

Ошибка.
Попробуйте повторить позже

Задача 8#129180Максимум баллов за задание: 7

1000 детей, среди которых нет двух одинакового роста, выстроились в шеренгу. Назовём пару различных детей $(a,b)$ хорошей, если между ними не стоит ребёнка, рост которого больше роста одного из $a$ и $b,$ но меньше роста другого. Какое наибольшее количество хороших пар могло образоваться? (Пары $(a,b)$ и $(b,a)$ считаются одной и той же парой.)

Источники: ВСОШ, ЗЭ, 2024, 9.8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1.

Сразу нам непонятно, что делать, поэтому имеет смысл посмотреть на задачу для маленьких чисел, чтобы понять ответ и как устроен оптимальный пример.

Показать ответ и решение

Докажем, что в аналогичной задаче для шеренги из $2n$ детей наибольшее возможное количество хороших пар равно $2 (n+ 1)− 3.$

Пронумеруем детей числами $1,2,$ $...,2n$ в порядке убывания роста. Тогда, если расставить детей в порядке

n +1,n+ 2,...,2n, 1,2,...,n,

то все пары $(i,j),$ где $i≤ n <j,$ окажутся хорошими; таких пар всего $n2.$ Кроме этого, все пары вида $(i,i+ 1)$ также окажутся хорошими; таких пар всего $2n− 1.$ При этом пара $(n,n +1)$ учтена дважды, так что общее количество хороших пар равно

2 2 n +(2n− 1)− 1 =(n+ 1)− 3.

Осталось доказать, что хороших пар не может быть больше, чем $(n+ 1)2− 3.$ Сделаем это индукцией по $n.$ При $n =1$ утверждение тривиально, ибо есть всего одна пара детей.

Пусть теперь $n> 1.$ Рассмотрим произвольную шеренгу и выберем в ней хорошую пару $(a,b),$ в которой $|a − b|$ — наибольшее; пусть для определённости $a< b,$ и ребёнок $a$ стоит левее, чем $b.$ Назовём ребёнка $c$ прекрасным, если он образует хорошие пары как с $a,$ так и с $b.$

______________________________________________________________________________________________________________________________________________________

Лемма. Существует не больше двух прекрасных детей.

Доказательство. Если $c$ прекрасен, то по выбору пары $(a,b)$ имеем $c− a ≤b− a$ и $b− c≤ b− a,$ откуда $a< c<b.$ Такой ребёнок $c$ не может стоять между $a$ и $b,$ иначе пара $(a,b)$ не была бы хорошей; значит, любой прекрасный ребёнок стоит либо слева от $a,$ либо справа от $b.$

Предположим, что есть два прекрасных ребёнка $c1 < c2,$ стоящих левее $a;$ тогда

a< c1 <c2 < b.

Ребёнок $c 1$ не может стоять между $a$ и $c, 2$ иначе пара $(a,c) 2$ не хорошая; поэтому $c 1$ стоит левее $c. 2$ Но тогда $c 2$ стоит между $c 1$ и $b,$ и пара $(c,b) 1$ — не хорошая, что невозможно. Это противоречие показывает, что левее $a$ стоит не более одного прекрасного ребёнка. Аналогично, не более одного стоит правее $b,$ откуда и следует доказываемое утверждение.

_________________________________________________________________________________________________________________________________________________________________________________

Теперь несложно совершить переход индукции. Выкинув $a$ и $b,$ мы получим, что все хорошие пары, не содержащие $a$ и $b,$ остались хорошими; по предположению индукции, их не больше, чем $n2 − 3.$ Осталось оценить количество хороших пар, содержащих $a$ или $b.$ Это пара $(a,b),$ пары $(a,c)$ и $(b,c)$ для любого прекрасного ребёнка $c,$ и максимум по одной из пар $(a,c)$ и $(b,c)$ для остальных детей $c.$ Всего получаем не более чем