Тема Закл (финал) 9 класс

Закл 2023

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 9 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83197Максимум баллов за задание: 7

Рассмотрим все 100-значные числа, делящиеся на 19.

Докажите, что количество таких чисел, не содержащих цифр 4,5 и 6, равно количеству таких чисел, не содержащих цифр 1, 4 и 7.

Источники: Финал ВсОШ - 2023, 9.6, автор И.А. Ефремов (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

В задаче просят доказать, что какие-то 2 множества равны. Попробуйте сделать биекцию между элементами множества.

Подсказка 2

Как делать биекцию между числами совсем непонятно. Попробуйте придумать биекцию так, чтобы друг в друга переходили цифры. Так чтобы запрещенные цифры переходили друг в друга. Как это можно сделать, уследив за делимостью на 19?

Подсказка 3

Предлагается операцией умножить цифру на что-нибудь. При такой операции делимость на 19 сохранится(поймите это). Как сделать в обратную сторону?

Показать доказательство

Каждому остатку $a$ от деления на 19 сопоставим остаток $b(a)$ такой, что $b(a) ≡ 3a. 19$

Заметим, что остаткам $0,1,2,3,7,8,9$ сопоставлены остатки $0,3,6,9,2,5,8$ соответственно. Более того, по остатку $b$ восстанавливается остаток $a =a(b) ≡19 −6b$ такой, что $a(b(a)) ≡19− 18a ≡19a$ и $b(a(b))=b$ (из аналогичных соображений).

Обозначим теперь через $𝒜$ множество чисел из условия, не содержащих цифр $4,5,6$ , а через $ℬ$ — множество таких чисел, не содержащих $1,4,7$ . Каждому числу $--------- A= a99a98...a0 ∈ 𝒜$ сопоставим число $---------------- B = b(a99)b(a98)...b(a0)$ . Заметим, что $b(ai)$ — цифра (причём $b(a99)⁄= 0$ ), так что получилось 100 -значное число. Кроме того,

99 B = b0+ 10b1+ ...+(10 b99 ≡ ) ≡ 3a0+ 10a1+...+1099a99 = 3A (mod19),

так что $B$ делится на 19 и $B ∈ ℬ$ . Поскольку разным числам из $𝒜$ соответствуют разные числа из $ℬ$ , количество чисел в $ℬ$ не меньше, чем в $𝒜$ .

Наконец, каждому числу $--------- B =b99b98...b0 ∈ℬ$ соответствует число $---------------- A= a(b99)a(b98)...a(b0)$ , которое по аналогичным причинам лежит в $𝒜$ . Отсюда следует, что количества чисел в $𝒜$ и $ℬ$ равны.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#131888Максимум баллов за задание: 7

Даны два приведённых квадратных трёхчлена $f(x)$ и $g(x);$ известно, что трёхчлены $f(x)$ , $g(x)$ и $f(x)+g(x)$ имеют по два корня. Оказалось, что разность корней трёхчлена $f(x)$ равна разности корней трёхчлена $g(x).$ Докажите, что разность корней трёхчлена $f(x)+g(x)$ не больше этих разностей. (В каждой разности из большего корня вычитается меньший.)

Источники: ВСОШ, ЗЭ, 2023, 9.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Любой приведённый квадратный трёхчлен с двумя корнями можно записать в виде (x – p)² – q² для некоторых p, q. Чему равна разность его корней и наименьшее значение в этих терминах?

Подсказка 2:

Разность равна 2q, а наименьшее значение –q². Чтобы сделать такие же рассуждения с f(x) + g(x), стоит рассмотреть трёхчлен (f(x) + g(x)) / 2. Он приведённый и имеет те же корни, что и f(x) + g(x).

Подсказка 3:

Попробуйте сначала оценить минимальное значение (f(x) + g(x)) / 2, а потом перейти к разности корней.

Показать доказательство

Первое решение. Заметим, что разность корней приведённого квадратного трёхчлена $x2 +bx+ c$ равна корню из его дискриминанта, то есть $√-2--- b − 4c.$

Пусть два данных трёхчлена — это

2 f(x)=x + b1x+c1

2 g(x)= x + b2x+ c2.

Согласно условию, у них общий дискриминант

D= b2− 4c = b2− 4c . 1 1 2 2

Вместо суммы трёхчленов удобно рассмотреть их полусумму — она тоже является приведённым квадратным трёхчленом. Квадрат разности его корней (то есть дискриминант) равен:

(b1+-b2)2 b21-+b22 (b1−-b2 )2 2 − 2(c1 +c2)= 2 − 2(c1+ c2)− 2 .

Значит, он не больше, чем

2 2 b1+-b2− 2(c1+ c2)= D-+ D-= D. 2 2 2

Отсюда и следует, что разность корней полусуммы не больше, чем $√D,-$ то есть разность корней каждого из данных трёхчленов.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Заметим, что любой приведённый квадратный трёхчлен с двумя корнями имеет вид

(x − p)2− q2

при $q ≥ 0.$ При этом разность его корней равна $2q,$ а его наименьшее значение равно $− q2.$

Теперь условие означает, что два данных трёхчлена имеют равные наименьшие значения $− q2.$ Наименьшее значение их полусуммы, очевидно, не меньше $− q2$ (оно является полусуммой каких-то значений исходных трёхчленов), то есть оно равно $− r2$ при $0≤ r≤ q.$ Поэтому и разность корней полусуммы, то есть $2r,$ не превосходит $2q.$

Ошибка.
Попробуйте повторить позже

Задача 3#131889Максимум баллов за задание: 7

Изначально в строку выписывают 250 букв — 125 букв A и 125 букв B в некотором порядке. Затем за одну операцию можно взять любой кусок из нескольких подряд стоящих букв, среди которых поровну букв A и B, и переставить буквы в этом куске в обратном порядке, поменяв в этом куске все буквы A на буквы B и буквы B на буквы A. (Например, из строки ABABBAB можно одной операцией получить строку ABBAABAB.) Можно ли выписать исходную строку и совершить несколько операций так, чтобы в результате на доске оказалась та же строка, буквы которой записаны в обратном порядке?

Источники: ВСОШ, ЗЭ, 2023, 9.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте найти какой-нибудь инвариант для операции из условия.

Подсказка 2:

Можно посмотреть на количество букв, обладающих каким-либо свойством.

Подсказка 3:

Обратите внимание на количество букв А на нечётных позициях. Как оно меняется при проведении операции?

Показать ответ и решение

Первое решение. Пронумеруем позиции в строке слева направо числами от 1 до 250. Пусть в исходной строке $x$ букв A стоят на нечётных местах (т. е. местах с нечётными номерами). Покажем, что в полученных строках это количество не изменится.

Действительно, пусть для некоторой операции выбран кусок, в котором по $y$ букв A и B, причём $t$ из этих букв A стоят на нечётных местах. Тогда на чётных местах в куске стоят $y− t$ букв A и, следовательно, $y− (y− t)= t$ букв B. После операции именно из этих $t$ букв B возникнут буквы A, стоящие на нечётных местах куска — значит, количество таких букв A не поменяется.

Итак, в любой полученной строке будет ровно $x$ букв A на нечётных местах. Однако, если строка развернётся задом наперёд, то на нечётных местах должны оказаться ровно те буквы, которые раньше были на чётных местах, а там было ровно $125− x$ букв A. Поскольку $125− x⁄= x,$ требуемое невозможно.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. В строке всего $1252$ пар, состоящих из буквы A и буквы B. Назовём такую пару левой, если в ней A стоит левее B, и правой иначе. Покажем, что при операции количество левых пар не изменяется. Из этого будет следовать невозможность требуемого, ибо при развороте строки все пары меняют тип, а значит, количество левых пар меняет чётность.

Рассмотрим одну операцию с куском длины $2y.$ При этой операции пары из букв, не лежащих в куске, сохраняют свой тип. Далее, для каждой буквы вне куска было ровно $y$ пар, содержащих её и букву из куска; столько же таких пар осталось, и все эти пары были и стали одного и того же типа.

Значит, осталось проследить за парами букв в самом куске. Но каждая пара сменила свой тип дважды: когда кусок развернулся и когда все буквы заменили на другие. Значит, количество левых пар в куске также не изменилось.

Ответ:

нельзя

Ошибка.
Попробуйте повторить позже

Задача 4#131890Максимум баллов за задание: 7

Каждое натуральное число, большее 1000, окрасили либо в красный, либо в синий цвет. Оказалось, что произведение любых двух различных красных чисел — синее. Может ли случиться, что никакие два синих числа не отличаются на 1?

Источники: ВСОШ, ЗЭ, 2023, 9.3 (см. olympiads.mccme.ru)

Показать ответ и решение

Первое решение. Предположим противное. Пусть существует такая раскраска натуральных чисел больше 1000 в красный и синий цвета, что произведение любых двух различных красных чисел синее, и никакие два синих числа не отличаются на 1.

Если число $n$ синее, то числа $n− 1$ и $n+ 1$ обязаны быть красными. Тогда их произведение $2 (n − 1)(n +1)= n − 1$ должно быть синим, а значит, $2 n$ должно быть красным.

Возьмём любое синее число $k> 1001.$ Тогда $2 k$ красное. Если $3 k$ синее, то $6 32 k =(k )$ красное. Но $6 2 4 k = k ⋅k,$ где $2 k$ и $6 k$ красные, значит, $4 k$ должно быть синим. Тогда $8 42 k =(k )$ красное, но $8 2 6 k = k ⋅k$ — произведение красных чисел, что невозможно.

Если же $3 k$ красное, то $5 2 3 k =k ⋅k$ синее, а $10 52 k =(k )$ красное. Так как

k10 = k2⋅k8 = k3 ⋅k7,

где $2 k$ и $3 k$ красные, то $7 k$ и $8 k$ должны быть синими. Тогда $14 7 2 k = (k)$ и $16 82 k = (k)$ красные, но $16 2 14 k =k ⋅k$ — произведение красных чисел, что приводит к противоречию.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Предположим, что такая раскраска существует. Если $a$ и $b$ различные красные числа, то $ab$ синее, а $ab+ 1$ красное.

Цвета не могут строго чередоваться по чётности, поэтому найдутся два красных числа $a$ и $a+ 1$ одинаковой чётности. Тогда $b= a(a+1)+ 1$ красное,

c= ab+ 1= a3+a2+ a+ 1

красное, а

4 3 2 d= (a+ 1)c=a + 2a +2a + 2a+ 1

синее.

С другой стороны,

p =(a+ 1)b+ 1= a3+ 2a2+ 2a+ 2

красное, значит,

ap =a4+ 2a3+2a2+ 2a= d− 1

синее. Получаем соседние синие числа $d$ и $d− 1,$ что противоречит условию.

Ответ:

не может

Ошибка.
Попробуйте повторить позже

Задача 5#131891Максимум баллов за задание: 7

Точка $X$ лежит строго внутри описанной около треугольника $ABC$ окружности. Обозначим через $I B$ и $I C$ центры внеописанных окружностей этого треугольника, касающихся сторон $AC$ и $AB$ соответственно. Докажите, что

XIB ⋅XIC > XB ⋅XC.

Источники: ВСОШ, ЗЭ, 2023, 9.4 (см. olympiads.mccme.ru)

Показать доказательство

Обозначим через $Γ$ окружность с диаметром $II . B C$ Поскольку $CI ⊥CI C B$ и $BI ⊥ BI , C B$ точки $B$ и $C$ лежат на $Γ .$

Обозначим через $I$ центр вписанной окружности треугольника $ABC.$ Если точка $X$ лежит внутри угла $BIC,$ то углы $XBIC$ и $XCIB$ тупые, поэтому:

XIB >XC, XIC > XB.

Перемножив эти неравенства, получим:

XIB ⋅XIC > XC ⋅XB.

$PIC$

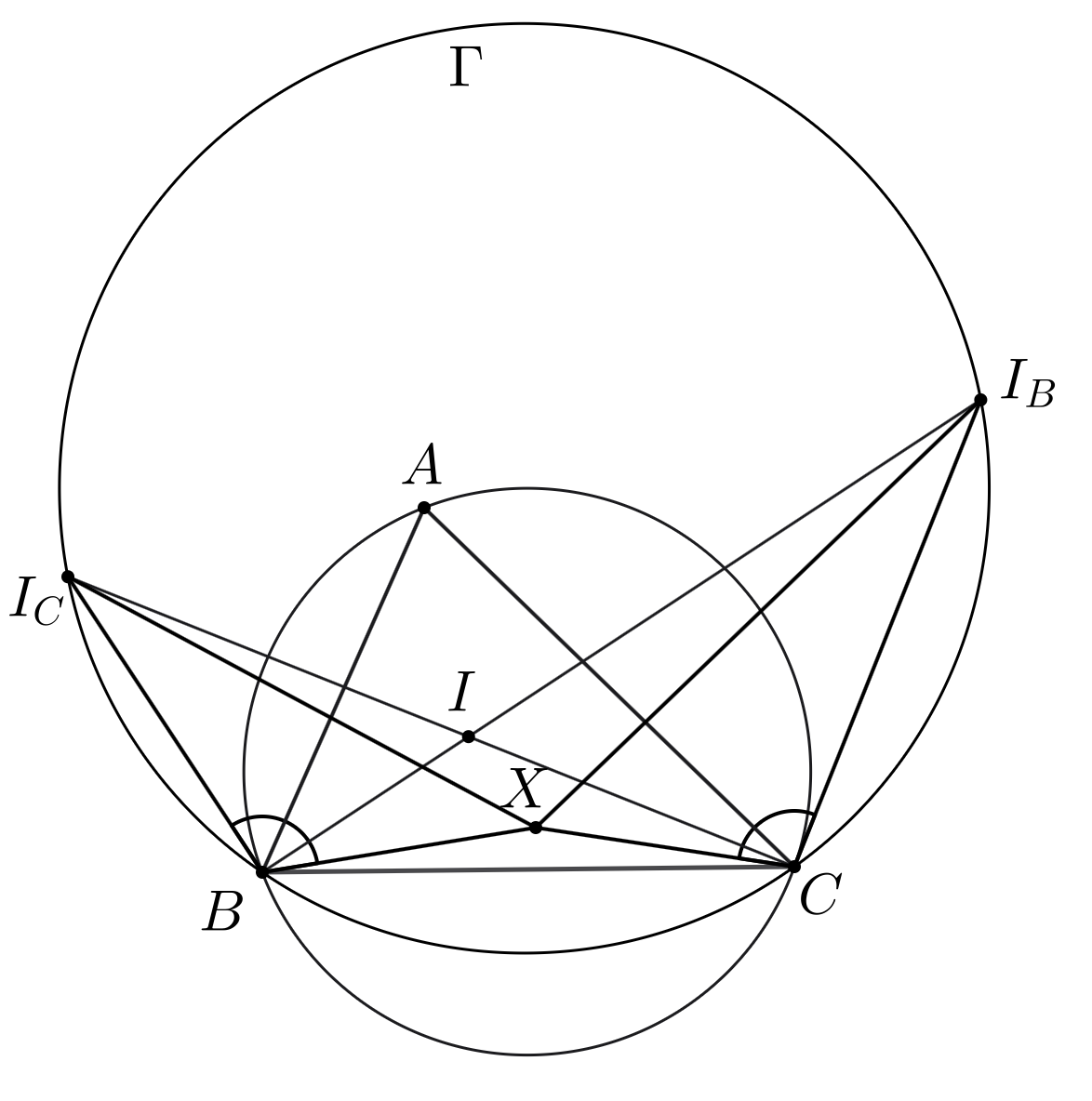
В противном случае точки $X$ и $A$ лежат в одной полуплоскости относительно прямой $BC.$ Продлим лучи $CX$ и $IBX$ до пересечения с $Γ$ в точках $C1$ и $Y$ соответственно.

Поскольку четырёхугольник $AICBI$ вписан в окружность с диаметром $IIC,$ имеем:

∠XC1B =∠IICB = ∠IAB = 12∠CAB,

а также

1 1 1 2∠CAB < 2∠CXB = 2(∠XC1B +∠XBC1 ).

Отсюда следует: $∠XC1B <∠XBC1,$ а значит, $XC1 > XB.$

$PIC$

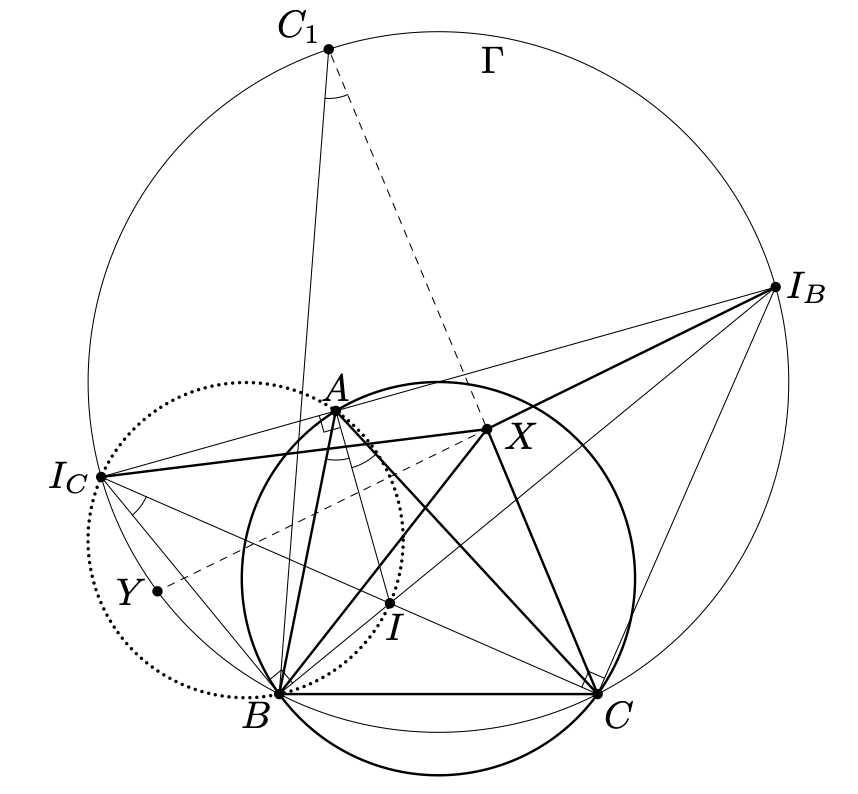
Кроме того, поскольку длина хорды окружности не превосходит длины диаметра:

IBX + XIC ≥ IBIC ≥ IBY =IBX + XY,

откуда $XIC > XY.$

Следовательно:

XIB ⋅XIC ≥XIB ⋅XY = XC ⋅XC1 >XC ⋅XB.

Ошибка.
Попробуйте повторить позже

Задача 6#131956Максимум баллов за задание: 7

Если на столе лежит несколько кучек камней, считается, что на столе много камней, если можно найти 50 кучек и пронумеровать их числами от 1 до 50 так, что в первой кучке есть хотя бы один камень, во второй — хотя бы два камня, …, в пятидесятой — хотя бы пятьдесят камней. Пусть исходно на столе лежат 100 кучек по 100 камней в каждой. Найдите наибольшее $n ≤10000$ такое, что после удаления из исходных кучек любых $n$ камней на столе всё равно останется много камней. (При удалении камней кучка не распадается на несколько.)

Источники: ВСОШ, ЗЭ, 2023, 9.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Хочется получить сначала хотя бы какую-то оценку, чтоб понимать, в каком направлении двигаться. Какая самая простая ситуация, когда на столе не "много камней"?

Подсказка 2:

Когда на столе просто нет 50 кучек, то есть их ≤ 49. Сколько камней необходимо удалить, чтоб осталось ≤ 49 кучек?

Подсказка 3:

51 * 100 = 5100, то есть имеем оценку на 5099. Пока что остановимся. Подумаем, как вообще можно доказать, что существует требуемая нумерация кучек?

Подсказка 4:

Пока что не особо ясно. Можно попробовать ввести обозначения, хуже точно не будет) Пусть 0 ≤ a₁ ≤ a₂ ≤ ... ≤ a₉₉ ≤ a₁₀₀ ≤ 100 — количество камней в кучках после удаления какого-то количества камней. Как проверить много ли камней на столе?

Подсказка 5:

Проверить, подходят ли кучки a₅₁, ..., a₁₀₀ под нумерацию (осознайте)? То есть хотим доказать, что a₅₁ ≥ 1, a₅₂ ≥ 2, ..., a₁₀₀ ≥ 50 или же a₅₀₊ᵢ ≥ i. Доказывать, что можно, хотя мы ещё до конца не знаем оценку — так себе идея. Как нужно поменять логику рассуждений?

Подсказка 6:

Необходимо предположить противное и понять, при каком минимальном количестве удалённых камней нельзя выполнить нумерацию. Тогда наша итоговая оценка будет зажата в промежутке. Итак, предположим противное, что получаем?

Подсказка 7:

Для некоторого i a₅₀₊ᵢ ≤ i − 1. Как это влияет на предыдущие кучки?

Подсказка 8:

Во всех предыдущих кучках ≤ i − 1 камней. То есть всего в них ≤ (50 + i) * (i − 1). Сколько же тогда в них отсутствует камней?

Подсказка 9:

Осознайте самостоятельно, что удалено ≥ 5100 камней. Кажется, осталось сделать совсем немного. Мы в Вас верим!

Показать ответ и решение

Если удалить полностью 51 кучку, то, очевидно, не останется много камней. Значит, искомое значение $n$ меньше 5100. (Альтернативно, можно удалить из всех кучек по 51 камню.)

Осталось показать, что при удалении любых $n = 5099$ камней останется много камней. Пусть в кучках осталось $a1,a2,$ …, $a100$ камней соответственно; можно считать, что

0≤a1 ≤a2 ≤ ⋅⋅⋅≤ a100 ≤ 100

Покажем, что $ai+50 ≥ i$ при $i= 1,2,$ …, $50,$ то есть кучки с номерами от 51 до 100 удовлетворяют требованию.

Пусть это не так, то есть $a ≤ i− 1 i+50$ при некотором $i≤ 50.$ Это значит, что каждая из первых $i+50$ кучек содержит не более $i− 1$ камней, то есть из неё удалено хотя бы $101− i$ камней. Поэтому общее количество удалённых камней не меньше, чем

(i+50)(101− i)= 5100− (i− 1)(i− 50)≥5100

Противоречие.

Ответ:

$n =5099$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#131957Максимум баллов за задание: 7

Дана трапеция $ABCD,$ в которой $AD ∥BC,$ а лучи $AB$ и $DC$ пересекаются в точке $G.$ Общие внешние касательные к окружностям, описанным около треугольников $ABC$ и $ACD,$ пересекаются в точке $E.$ Общие внешние касательные к окружностям, описанным около треугольников $ABD$ и $BCD,$ пересекаются в точке $F.$ Докажите, что точки $E,F$ и $G$ лежат на одной прямой.

Источники: ВСОШ, ЗЭ, 2023, 9.7 и 10.7 (см. olympiads.mccme.ru)

Показать доказательство

Пусть прямая $EC$ повторно пересекает окружность $(ABC )$ в точке $X,$ а прямая $EA$ повторно пересекает окружность $(ACD )$ в точке $Y$ (мы разберём расположение точек, указанное на рисунке; другие случаи рассматриваются аналогично).

Рассмотрим гомотетию с центром $E,$ переводящую $(ABC)$ в $(ACD).$ При такой гомотетии точка $X$ переходит в $C,$ а точка $A$ — в $Y.$ Отсюда $AX ∥CY$ и

∠AEC = ∠AY C− ∠ECY = ∠AYC − ∠AXC.

Но $∠AXC =180∘− ∠ABC$ и $∠AY C = 180∘− ∠ADC.$ Значит,

∠AEC =∠ABC − ∠ADC =∠ABC − ∠BCG =∠BGC.

Из полученного равенства следует, что точки $A,$ $C,$ $E,$ $G$ лежат на одной окружности.

$PIC$

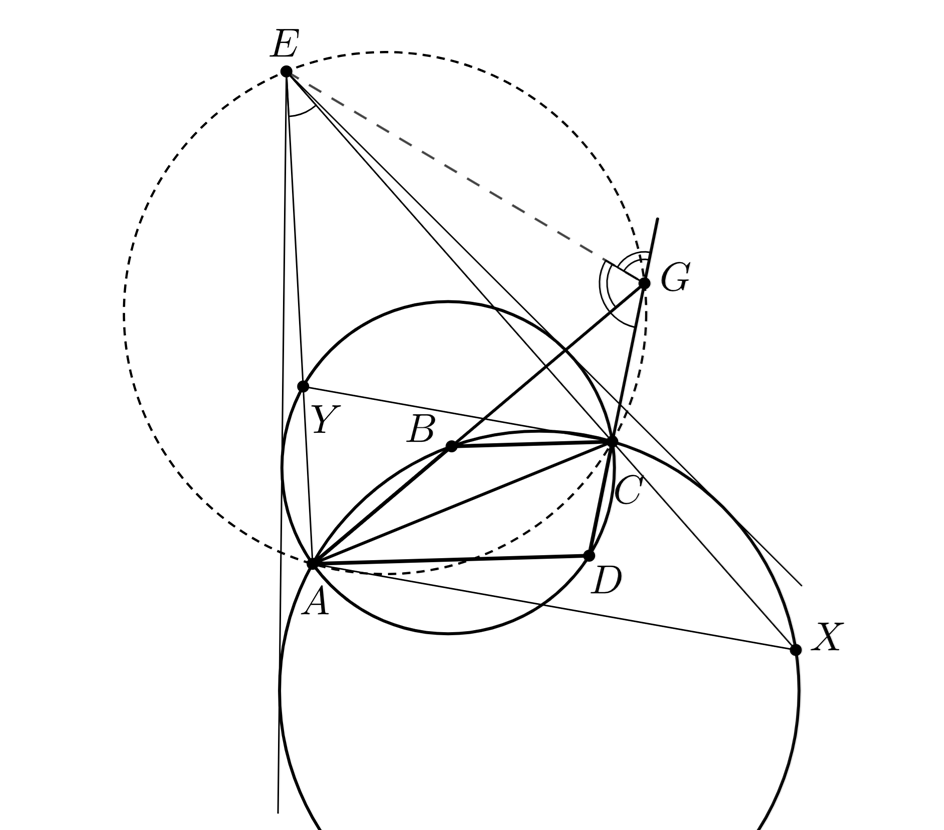
Поскольку точка $E$ лежит на серединном перпендикуляре к $AC$ (т.е. на оси симметрии окружностей $(ABC )$ и $(ACD )$ ), она является серединой дуги $AGC$ окружности $(ACEG ).$ Значит, $E$ лежит на внешней биссектрисе угла $BGC.$

Аналогично показывается, что $F$ также лежит на внешней биссектрисе угла $BGC.$

______________________________________________________________________________________________________________________________________________________

Замечание. У задачи есть следующее обобщение. Пусть $ABCD$ — четырёхугольник, $G =AB ∩ CD,$ а $M$ — вторая точка пересечения окружностей $(ADG )$ и $(BCG )$ (иначе говоря, точка Микеля этого четырёхугольника). Пусть $E$ — центр гомотетии с положительным коэффициентом, переводящей $(ABC )$ в $(ADC ).$ Тогда точки $A,$ $C,$ $M,$ $E$ лежат на одной окружности, причём $E$ — середина дуги $AC$ (т.е. $ME$ — биссектриса угла между $AM$ и $CM$ ).

Доказать это можно аналогично решению задачи: имеем (в направленных углах)

∠AEC = ∠ABC +∠ADC = ∠GBC +∠AMG = ∠GMC +∠AMG = ∠AMC.

Ошибка.
Попробуйте повторить позже

Задача 8#131958Максимум баллов за задание: 7

У Пети есть 10 000 гирь, среди них нет двух гирь равного веса. Также у него есть чудо-прибор: если положить в него 10 гирь, он сообщит сумму весов каких-то двух из них (при этом неизвестно, каких именно). Докажите, что Петя может использовать чудо-прибор так, чтобы через некоторое время указать на одну из гирь и точно назвать её вес. (В чудо-прибор нельзя класть другое количество гирь.)

Источники: ВСОШ, ЗЭ, 2023, 9.8 (см. olympiads.mccme.ru)

Показать доказательство

Покажем, что Петя сможет определить вес одной гири, даже если у него 8000 гирь. Положим $n =4000.$

______________________________________________________________________________________________________________________________________________________

Лемма. Для любых $n$ гирь Петя может найти две гири, для которых он знает их суммарный вес.

Доказательство. Пусть Петя положит в прибор по очереди все возможные наборы из 10 гирь из наших $n.$ Заметим, что каждое показание прибора — это вес какой-то из $2 C n$ пар гирь (будем говорить, что это показание использует эту пару). В то же время, Петя получит $10 Cn$ показаний. Значит, одна из пар будет использована хотя бы

C10 (n− 2)(n− 3)...(n − 9) D = Cn2n-= -----3⋅4⋅...⋅10-----

раз.

Иначе говоря, найдутся $D$ измерений таких, что (1) в них прибор показывает один и тот же вес $S,$ и (2) во всех десятках, использованных в этих испытаниях, есть две общих гири $a$ и $b.$ Мы покажем, что при выполнении условий (1) и (2) суммарный вес $a$ и $b$ обязательно равен $S,$ то есть вес этой пары Петя и сможет определить по показаниям прибора. Назовём десятки, использованные в этих $D$ измерениях, нужными.

Предположим противное: сумма весов $a$ и $b$ не равна $S.$ Рассмотрим все пары из $n$ гирь, суммы весов в которых равны $S$ (назовём эти пары хорошими). Поскольку веса всех гирь различны, хорошие пары не пересекаются; в частности, их не больше, чем $n∕2.$ При этом в каждой нужной десятке есть не только гири $a$ и $b,$ но и хотя бы одна хорошая пара. Оценим теперь общее количество нужных десяток.

Пусть в нужной десятке хорошая пара не содержит ни $a,$ ни $b.$ Любую такую десятку можно получить, добавив к гирей $a$ и $b$ хорошую пару (не более чем $(n− 2)∕2$ способами), а затем дополнив шестью из оставшихся $n− 4$ гирь. Итого, количество таких десятков не больше, чем $n−2C6 . 2 n−4$

Во всех остальных нужных десятках хорошая пара содержит либо $a,$ либо $b.$ Если есть хорошая пара, содержащая $a,$ то для получения нужной десятки, содержащей эту пару, её надо дополнить гирей $b$ и ещё семью гирами из оставшихся $n − 3.$ Итого, таких нужных десяток не больше $C7 . n−3$ Аналогично, нужных десяток, содержащих хорошую пару с гирей $b,$ тоже не больше $C7 . n−3$

Итого, получаем

n−-2 6 7 (7-⋅8-⋅9-⋅10 8-⋅9-⋅10) ( 1 1) D ≤ 2 Cn−4+ 2C n− 3 =D ⋅ 4(n− 3) + n − 2 < D⋅ 2 + 2 = D.

Противоречие.

_________________________________________________________________________________________________________________________________________________________________________________

Завершим решение задачи. Построим следующий граф. Сопоставим каждой гире вершину. Среди каждых $n$ гирь найдём одну пару с известной суммой; две соответствующих вершины соединим ребром. Если в этом графе нет нечётных циклов, то, как известно, его вершины можно раскрасить в два цвета так, чтобы каждое ребро соединяло вершины разных цветов. Но тогда вершины одного цвета не меньше $n,$ и потому среди них мы провели ребро; противоречие.

Значит, в полученном графе есть цикл $w1,w2,$ …, $w2k+1,$ и Петя знает суммарные веса всех пар соседних гирь в этом цикле. Взяв полусумму всех этих весов, Петя узнает суммарный вес всех гирь цикла. Вычтя из него

(w2 +w3)+ (w4+ w5)+ ⋅⋅⋅+ (w2k +w2k+1),

он узнает вес гири $w1.$