Тема Закл (финал) 9 класс

Закл 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 9 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68251Максимум баллов за задание: 7

Биссектрисы треугольника $ABC$ пересекаются в точке $I$ , внешние биссектрисы его углов $B$ и $C$ пересекаются в точке $J$ . Окружность $ωb$ с центром в точке $Ob$ проходит через точку $B$ и касается прямой $CI$ в точке $I.$ Окружность $ωc$ с центром в точке $Oc$ проходит через точку $C$ и касается прямой $BI$ в точке $I.$ Отрезки $ObOc$ и $IJ$ пересекаются в точке $K.$ Найдите отношение $IK :KJ$ .

Источники: Всеросс., 2022, ЗЭ, 9.2(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Проведём окружность ω, описанную около треугольника ABC. Попробуйте рассмотреть случай, когда окружность ωb пересекает окружность ω в двух точках, причем второй раз в точке P.

Подсказка 2

Пусть CI пересекает AB в точке L. Тогда по теореме об угле между касательной и хордой ∠BPI=∠BIL, а ∠BIL=∠IBC+∠ICB=90°-∠BAC / 2. Пускай PI пересекает окружность ω повторно в точке N. Что можно сказать про точку N?

Подсказка 3

Т.к. ∠BPI=90°-∠BAC / 2, то и ∠BPN=90°-∠BAC / 2. Отсюда следует, что N- середина дуги BAC. Заметим, что все переходы были равносильными, поэтому окружность ωb действительно повторно пересекает окружность ω в точке P. А в какой точке будет пересекать её окружность ωc?

Подсказка 4

В той же самой точке P! Ведь P определяется как пересечение окружности ω с прямой NI. А точки B и C равноправны относительно прямой NI и окружности ω. Пусть прямая AJ пересекает ω в точке S. Тогда NS- диаметр ω => NPS - прямой. В каком отношении тогда ObOc делит IP?

Подсказка 5

Пусть ObOc пересекает IP в точке Z. Т.к. линия центров перпендикулярна общей хорде и делит её пополам, то IZ=ZP и ObOc параллельна SP. Тогда прямая ObOc делит пополам IS. Осталось только вспомнить про лемму о трезубце, найти отношение IS/SJ и завершить решение!

Показать ответ и решение

Первое решение.

Проведём в окружности $ωb$ диаметр $IX$ , а в окружности $ωc−$ диаметр $IY$ . Заметим, что $∘ ∠IBJ = 90 =∠ICJ$ , поскольку внутренняя и внешняя биссектриса угла перпендикулярны. Следовательно, точка $X$ лежит на $BJ$ , а точка $Y$ - на $CJ$ .

$PIC$

Кроме того, $IX ⊥IC$ , поскольку $ωb$ касается $IC$ в точке $I$ , поэтому $IX∥CJ$ . Аналогично, $IY∥BJ$ . Итого, четырёхугольник $IXJY$ - параллелограмм, пусть его диагонали пересекаются в точке $S$ . Тогда $IS =SJ$ , а отрезок $ObOj$ - средняя линия треугольника $IXY$ , поэтому точка $K−$ середина отрезка $IS$ . Таким образом, $IK =IS∕2= IJ∕4$ , откуда следует, что $IK∕KJ = 1∕3$ .

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим через $N$ середину дуги $BAC$ описанной окружности $Ω$ треугольника $ABC$ , а через $S−$ середину другой её дуги $BC$ . Пусть луч $NI$ вторично пересекает $Ω$ в точке $P$ . Поскольку $SN$ - диаметр окружности $(ABC )$ , то $∠NP S =90∘$ .

По лемме о трезубце $S$ — середина отрезка $IJ$ . Поскольку $∠BAC =∠BNC$ и $BN =NC$ , то

1 1 ∠NBC =∠NCB = 2∠ABC + 2∠ACB

Продлим луч $CI$ до пересечения с $AB$ в точке $L$ .

$PIC$

Так как $∠LIB$ внешний для треугольника $BIC$ , а также четырёхугольник $BNCP$ - вписанный, мы получаем, что $∠LIB =$ $=∠IBC + ∠ICB = 12∠ABC + 12∠ACB = ∠NCB = ∠IPB$ , поэтому окружность $(IBP)$ касается прямой $CI$ в точке $I$ . Также эта окружность проходит через $B$ , следовательно, это и есть окружность $ωb$ . Аналогично, окружность $ωc$ описана около треугольника $IPC$ .

Значит, IP - общая хорда окружностей $ωb$ и $ωc$ , а тогда $ObOc−$ серединный перпендикуляр к отрезку $IP$ . Поскольку к тому же $∠IPS = 90∘$ , мы получаем, что $O1O2$ проходит через середину отрезка $IS$ , то есть $KI = KS$ , а тогда $IK ∕KJ =1∕3$ .

Ответ:

$1 :3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#78818Максимум баллов за задание: 7

Для какого наименьшего натурального числа $a$ существуют целые числа $b$ и $c$ такие, что квадратный трёхчлен $ax2+bx+ c$ имеет два различных положительных корня, не превосходящих $-1- 1000?$

Источники: Всеросс., 2022, ЗЭ, 9.6(см. olympiads.mccme.ru)

Показать ответ и решение

Первое решение. Докажем, что $a≥ 1001000.$ Заметим, что если $y$ —корень трёхчлена $ax2+bx+ c,$ то $1∕y$ —корень трёхчлена $2 cx + bx +a.$ Поэтому в задаче нужно найти наименьшее натуральное $a,$ для которого корни $x1$ и $x2$ некоторого трёхчлена $2 cx + bx +a$ (с целыми $b$ и $c$ ) больше $1000.$ Поскольку $x1$ и $x2$ положительны и $x1x2 =a∕c$ (по теореме Виета), имеем $c> 0.$

Если $c= 1,$ то $√ 2----- |x1− x2|= b − 4a≥ 1.$ Поскольку меньший корень не меньше $1000,$ больший корень не меньше $1001,$ а тогда $a= x1x2 ≥ 1001 ⋅1000.$ Если же $c≥2,$ то $a =cx1x2 ≥ 2x1x2 > 2000000.$ В обоих случаях требуемая оценка доказана.

Осталось заметить, что трёхчлен $2 x − (1000+ 1001)x +1001⋅1000$ имеет корни $1000$ и $1001,$ поэтому $a= 1001000$ подходит.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Положим для краткости $n =1000.$ Пусть $x1$ и $x2$ — два различных корня трёхчлена $f(x)= ax2+ bx +c,$ причём $0 <x1 < x2 ≤ 1n.$ Тогда число $b= −a(x1+x2)$ отрицательно, а число $c=ax1x2$ положительно. Более того, имеем $−ab= x1+ x2 < 2n,$ откуда $a> − nb2 .$

Поскольку корни различны, дискриминант $D = b2− 4ac$ положителен. Следовательно, $b2 > 4ac> −2nbc$ и, значит, $− b> 2nc.$ Поэтому $a> (−b)⋅ n2 > 2nc⋅ n2 = n2.c$ Пусть $a= n2c+d,$ где $d$ — натуральное число.

Предположим, что $a< n2+ n.$ Тогда $c= 1$ и $d< n.$ Стало быть,

( ) 0≤ f 1 = -a2 + b+ c= d2 + b +2 <-1+ b+ 2 n n n n n n n

и, значит, $− b< 2n+ 1.$ Следовательно, $− b≤ 2n$ и

D =b2− 4ac≤4n2− 4(n2+d)= −4d <0

Это противоречие показывает, что $d≥ n.$

Если же $a =n2+ n,$ то при $b=− 2n − 1$ и $c= 1$ трёхчлен имеет корни $x1 = -1- n+1$ и $x2 = 1. n$

Ответ:

$a =1001000$

Ошибка.
Попробуйте повторить позже

Задача 3#82257Максимум баллов за задание: 7

Дана бесконечная последовательность чисел $a ,a ,..., 1 2$ в которой нет двух равных членов. Отрезок $a,a ,...,a i i+1 i+m−1$ этой последовательности назовем монотонным отрезком длины $m,$ если выполнены неравенства $ai < ai+1 < ...< ai+m −1$ или неравенства $ai > ai+1 >...>ai+m−1.$ Оказалось, что для каждого натурального $k$ член $ak$ содержится в некотором монотонном отрезке длины $k+ 1.$ Докажите, что существует натуральное $N$ такое, что последовательность $aN ,aN+1,...$ монотонна, т. е. $aN < aN+1 < ...$ или $aN > aN+1 > ....$

Источники: ВСОШ, 2022, ЗЭ, 9.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте понять, какие ашки мешают построить нужную монотонную последовательность и как с ними бороться.

Подсказка 2:

Это ашки с "плохими" индексами, которые либо меньше обоих соседей, либо больше. Действительно, если их количество конечное, то тогда нужная последовательность есть. Значит, нужно предположить, что их бесконечно много, и найти противоречие. Как можно это сделать?

Подсказка 3:

Попробуйте выбрать некоторый плохой индекс k и взять произвольное n>k. Тогда рассмотрите монотонный отрезок длины n +1, содержащий a_n. Попробуйте раскрутить дальше до конца решения.

Показать доказательство

Первое решение. Будем называть индекс $k ≥2$ плохим, если $a < a > a k−1 k k+1$ или $a > a <a . k− 1 k k+1$ Заметим, что если среди индексов $N + 1,N + 2,...$ нет плохих, то последовательность $aN ,aN+1,aN+2,...$ монотонна.

Предположим, что утверждение задачи неверно. Тогда найдётся бесконечно много плохих индексов. Выберем некоторый плохой индекс $k.$ Возьмём произвольное $n> k$ и рассмотрим монотонный отрезок $I$ длины $n +1,$ содержащий $an.$ Он не может содержать членов $ak−1,ak$ и $ak+1$ одновременно; следовательно, поскольку $k+ 1≤ n,$ отрезок $I$ точно не содержит $ak−1,$ а следовательно, не содержит и $a1.$

Итак, монотонный отрезок $I$ длины $n+ 1$ содержит $an,$ но не содержит $a1;$ тогда он обязан содержать $an,an+1$ и $an+2,$ так что индекс $n+ 1$ не является плохим. Итак, при любом $n >k$ индекс $n +1$ не плохой, поэтому плохих индексов конечное количество. Противоречие.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Предположим противное. Не умаляя общности, можно считать, что $a1 <a2$ (иначе можно умножить все члены последовательности на $− 1$ ). Поскольку последовательность $a2,a3,...$ не является возрастающей, существует такое $k ≥2,$ что $ak > ak+1.$ Поскольку последовательность $ak+1,ak+2...$ не является убывающей, существует такое $ℓ> k,$ что $aℓ < aℓ+1.$ Выберем наименьшее $ℓ,$ удовлетворяющее этим двум неравенствам. Тогда либо $ℓ> k+ 1,$ и тогда $aℓ−1 > aℓ$ согласно выбору $ℓ,$ либо $ℓ =k +1,$ и тогда $aℓ−1 =ak >ak+1 = aℓ.$ Итак, в любом случае $aℓ−1 > aℓ.$

Рассмотрим монотонный отрезок длины $ℓ,$ содержащий $aℓ−1;$ он обязан содержать и $aℓ.$ Поскольку $aℓ−1 > aℓ,$ числа этого отрезка монотонно убывают. Значит, он не может содержать числа $a1$ (иначе бы он содержал и $a2 > a1$ ). Но тогда, раз длина отрезка равна $ℓ,$ он обязан содержать и $aℓ+1 >aℓ,$ что невозможно.

Ошибка.
Попробуйте повторить позже

Задача 4#84253Максимум баллов за задание: 7

В строку выписаны $200$ натуральных чисел. Среди любых двух соседних чисел строки правое либо в $9$ раз больше левого, либо в $2$ раза меньше левого. Может ли сумма всех этих $200$ чисел равняться $2022 24 ?$

Источники: Всеросс., 2022, ЗЭ, 9.3(см. olympiads.mccme.ru)

Показать ответ и решение

Пусть строка состоит из чисел $a,a ,...,a 1 2 200$ в этом порядке. Если число $a = 2k i$ чётно, то следующим за ним может быть число $k$ или число $18k;$ эти числа дают одинаковые остатки при делении на $17.$ Если же $ai$ нечётно, то $ai+1 = 9ai.$ В любом случае получаем, что $ai ≡ 2ai+1 (mod17).$

Таким образом, полагая $a =a200,$ получаем, что с точки зрения остатков при делении на $17$ строка устроена так же, как и строка $199 198 2 a,2 a,...,2a,a.$ Сумма всех членов этой новой строки равна $(200 ) 2 − 1a.$ В частности, она делится на $8 2 − 1= 15⋅17,$ то есть делится на $17.$ Поэтому и сумма чисел в исходной строке делится на $17,$ и она не может равняться $2022 24 .$

Ответ:

Не может

Ошибка.
Попробуйте повторить позже

Задача 5#137294Максимум баллов за задание: 7

Назовём главными делителями составного числа $n$ два наибольших его натуральных делителя, отличных от $n.$ Составные натуральные числа $a$ и $b$ таковы, что главные делители числа $a$ совпадают с главными делителями числа $b.$ Докажите, что $a =b.$

Источники: ВСОШ, ЗЭ, 2022, 9.1, 10.1 и 11.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Если известны главные делители, то можно найти и два наименьших делителя, отличных от 1.

Подсказка 2:

Какой смысл в их нахождении? Они устроены понятным образом. Меньший из них — наименьший простой делитель числа, а второй — либо преднаименьший, либо наименьший в квадрате. Можно ли в этих случаях однозначно восстановить число?

Показать доказательство

Пусть $n >k$ — главные делители числа $a;$ тогда $a n$ и $a k$ — два наименьших делителя числа $a,$ больших единицы. Пусть $p$ — наименьший простой делитель числа $a,$ а $q$ — наименьший простой делитель $a,$ кроме $p$ (если такой существует). Тогда $a∕n= p.$ Далее, $a∕k$ — либо простое число (тогда это $q$ ) либо составное. Во втором случае единственным простым делителем числа $a∕k$ является $p,$ и потому $2 a∕k= p;$ этот случай реализуется ровно тогда, когда $a$ делится на $2 p ,$ причём $2 p <q$ или $q$ не существует.

Итак, главные делители числа $a$ — это либо $a p$ и $a q,$ либо $a p$ и $a- p2.$ Покажем теперь, что по двум главным делителям $n >k$ составное число $a$ восстанавливается однозначно (откуда и следует требуемое). Если $n$ кратно $k,$ то выполнен второй случай, и тогда $n2 a =-k .$ Иначе выполнен первый случай, и тогда $a= HOK (n,k).$

Ошибка.
Попробуйте повторить позже

Задача 6#137295Максимум баллов за задание: 7

В классе 18 детей. Родители решили подарить детям из этого класса торт. Для этого они сначала узнали у каждого ребёнка площадь куска, который он хочет получить. После этого они заказали торт квадратной формы, площадь которого в точности равна сумме 18 названных чисел. Однако, увидев торт, дети захотели, чтобы их куски тоже были квадратными. Родители могут резать торт разрезами, параллельными сторонам торта (разрезы не обязаны начинаться или оканчиваться на стороне торта). Для какого наибольшего $k$ родители гарантированно могут вырезать из заказанного торта $k$ квадратных кусков, которые можно выдать $k$ детям, чтобы каждый из них получил желаемое?

Источники: ВСОШ, ЗЭ, 2022, 9.4 (см. olympiads.mccme.ru)

Показать ответ и решение

Мы всегда считаем, что площадь торта равна $1.$

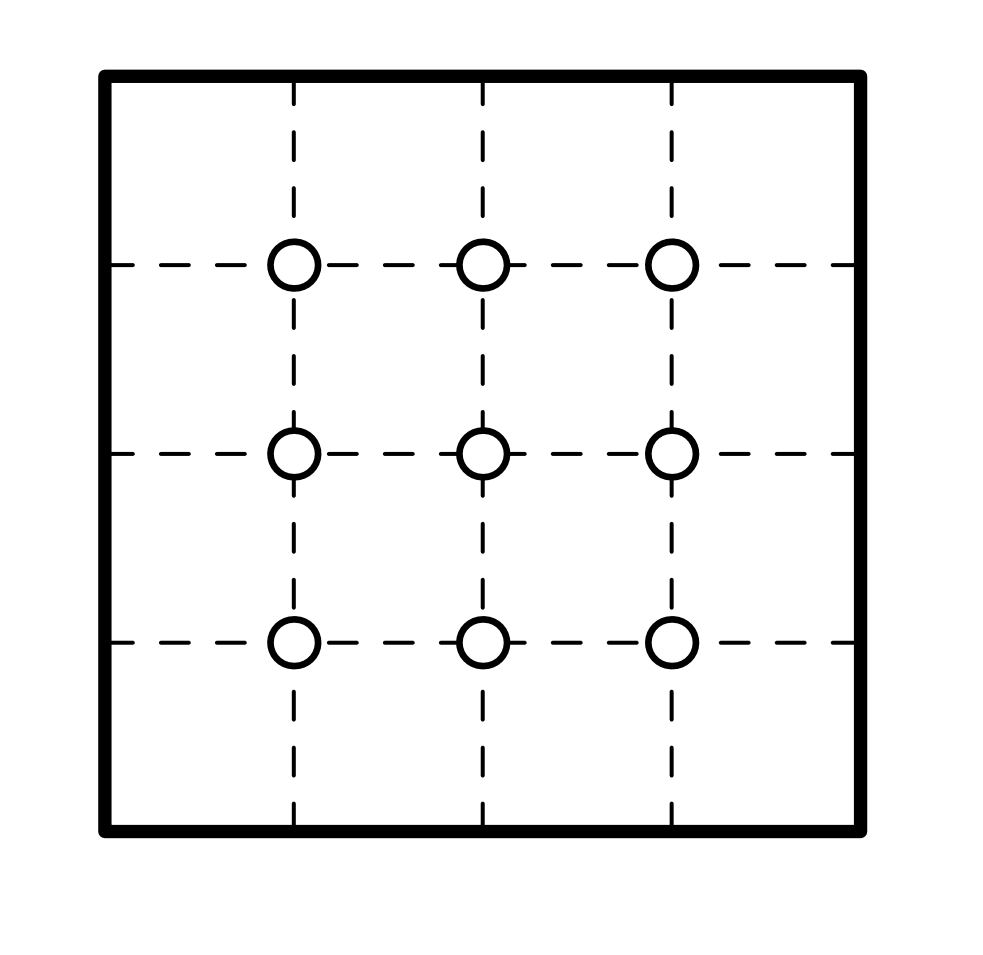
Покажем, что при некоторых запросах детей родители не смогут вырезать более $12$ требуемых кусков. Выберем число $1- 1- 15 > x> 16.$ Предположим, что $15$ главных детей заказали по куску торта площади $x$ (а остальные трое сделали произвольные заказы так, чтобы суммарная площадь заказанных кусков была равна 1). Мысленно разобьём торт на 16 равных квадратов и отметим на торте все 9 вершин этих квадратов, не лежащих на границе торта (см. рисунок ниже). Тогда строго внутри любого квадратного куска площади $x$ будет лежать одна из отмеченных точек, то есть можно вырезать не больше девяти таких кусков. Значит, хотя бы шестерым детям желаемых кусков не достанется.

$PIC$

Осталось доказать, что $12$ детей всегда смогут получить желаемое. Пусть

a1 ≥a2 ≥ ...≥ a18

— длины сторон кусков, которые хотят получить дети, то есть

a21+ a22+...+a218 = 1.

Покажем, что из квадрата можно вырезать куски со сторонами $a7,a8,...,a18.$

Для этого нам потребуются неравенства

a7 +a10+a13+ a16 ≤1 и a7+ a8+a9 ≤1. (∗)

Для доказательства первого неравенства заметим, что

1≥ a21+a22+ ...+ a216 ≥4a24+ 4a28 +4a212+4a216 ≥

≥4(a27+a210+ a213+ a216)≥ (a7+a10+ a13+ a16)2;

в последнем переходе мы воспользовались неравенством между средним квадратичным и средним арифметическим. Второе неравенство доказывается аналогично:

1≥ a21+ a22 +...+a29 ≥ 3a23+3a26+ 3a29 ≥

2 2 2 2 ≥ 3(a7+ a8+ a9)≥ (a7+a8+ a9).

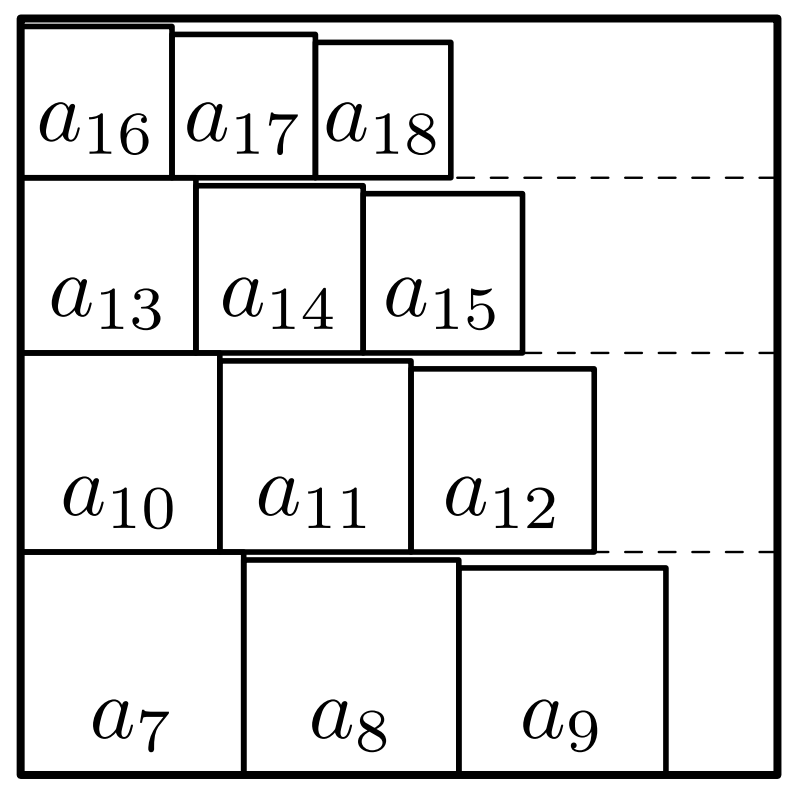
Из неравенств $(∗)$ следует, что можно разрезать торт на горизонтальные полосы высот, не меньших $a , 7$ $a , 10$ $a 13$ и $a 16$ соответственно, и в $i$ -ю полосу уложить квадраты со сторонами $a , 3i+4$ $a 3i+5$ и $a , 3i+6$ как показано на рисунке ниже.

$PIC$

Ответ:

$k =12$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#137300Максимум баллов за задание: 7

В стране 998 городов. Некоторые пары городов соединены двусторонними авиарейсами. Согласно закону, между любой парой городов должно быть не больше одного рейса. Другой закон требует, чтобы для любой группы городов было не больше $5k+ 10$ рейсов, соединяющих два города этой группы, где $k$ — количество городов в группе. В настоящий момент законы соблюдены. Докажите, что министерство развития может ввести несколько новых рейсов так, чтобы законы по-прежнему соблюдались, а общее количество рейсов в стране стало равным 5000.

Источники: ВСОШ, ЗЭ, 2022, 9.7 (см. olympiads.mccme.ru)

Показать доказательство

Назовём набор городов критическим, если есть $5k+ 10$ рейсов, соединяющих два города этой группы, где $k$ — количество городов в группе. Тогда $k >11,$ ибо иначе между городами группы есть не более

k(k− 1)∕2≤ 5k < 5k +10

рейсов. Если группа из всех 998 городов критическая, то в стране уже $5⋅998+10= 5000$ рейсов.

В дальнейшем мы всегда предполагаем, что законы в любой момент соблюдены. Обозначим через $f(X )$ количество рейсов, соединяющих два города группы $X.$

Докажем, что если группа из всех городов не критическая, то министерство может добавить один рейс с соблюдением законов. Повторяя такие операции, министерство добьётся требуемого. Заметим, что, если между городами $x$ и $y$ нет рейса, то добавить его министерство не может лишь в случае, когда оба города $x$ и $y$ входят в какую-то критическую группу.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Пусть $A$ и $B$ — критические группы. Тогда группа $A ∪B$ также критическая.

Доказательство. Положим

C = A∩ B,D= A ∪B.

Пусть

|A |= a,|B |= b,|C|= c;

тогда $|D|= a+b− c.$ По условию, имеем

f(A )=5a+ 10, f(B)= 5b+ 10, f(C)≤ 5c+ 10.

Заметим, что все рейсы, посчитанные в $f(A )$ и $f(B ),$ учитываются также и в $f(D);$ более того, если какой-то рейс учтён и в $f(A ),$ и в $f(B ),$ то оба его конца лежат в $C,$ то есть количество дважды учтённых рейсов равно $f(C).$ Поэтому

f(D )≥ f(A)+ f(B)− f(C)≥ (5a +10)+(5b+ 10)− (5c+ 10)=5(a+ b− c)+ 10 =5d+ 10.

Учитывая, что законы соблюдены, получаем $f(D) =5d+ 10,$ что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Вернёмся к решению. Если в настоящий момент нет ни одной критической группы, можно добавить рейс между любой парой городов, между которыми его ещё нет (такая пара найдётся!). Иначе, применяя лемму, получаем, что объединение всех критических групп — тоже критическая группа $A;$ по предположению, в ней $a< 998$ городов. Пусть $x$ — город вне $A;$ тогда $x$ не входит ни в какую критическую группу.

Пусть из $x$ идёт $k$ рейсов в города из $A.$ Поскольку группа $A′ = A∪ {x}$ не критическая, имеем

′ 5(a+1)+ 10> f(A )= f(A )+k= 5a+ 10+k,

откуда $k< 5.$ С другой стороны, $a≥ 12,$ поэтому в $A$ есть город $y,$ не соединённый рейсом с $x,$ и города $x$ и $y$ не входят в одну критическую группу. Значит, министерство может ввести рейс между $x$ и $y.$

Ошибка.
Попробуйте повторить позже

Задача 8#137301Максимум баллов за задание: 7

В треугольник $ABC$ вписана окружность $ω,$ касающаяся стороны $BC$ в точке $K.$ Окружность $ω′$ симметрична окружности $ω$ относительно точки $A$ . Точка $A0$ выбрана так, что отрезки $BA0$ и $CA0$ касаются $′ ω.$ Пусть $M$ — середина стороны $BC.$ Докажите, что прямая $AM$ делит отрезок $KA0$ пополам.

Источники: ВСОШ, ЗЭ, 2022, 9.8 (см. olympiads.mccme.ru)

Показать доказательство

Пусть точки $B′,$ $C′$ и $K′$ симметричны относительно $A$ точкам $B,$ $C$ и $K$ соответственно. Тогда окружность $ω′$ вписана в треугольник $′′ AB C$ и касается $′ ′ B C$ в точке $′ K .$ Медиана $AM$ является средней линией в треугольниках $′ BCC$ и $′ B BC,$ так что $′ ′ AM ∥BC ∥B C.$ Поскольку $A$ — середина $′ KK ,$ утверждение задачи равносильно тому, что прямая $AM$ содержит среднюю линию треугольника $′ KK A0$ (параллельную $′ A0K$ ), то есть утверждение равносильно параллельности $′ ′ B C ∥A0K .$

$PIC$

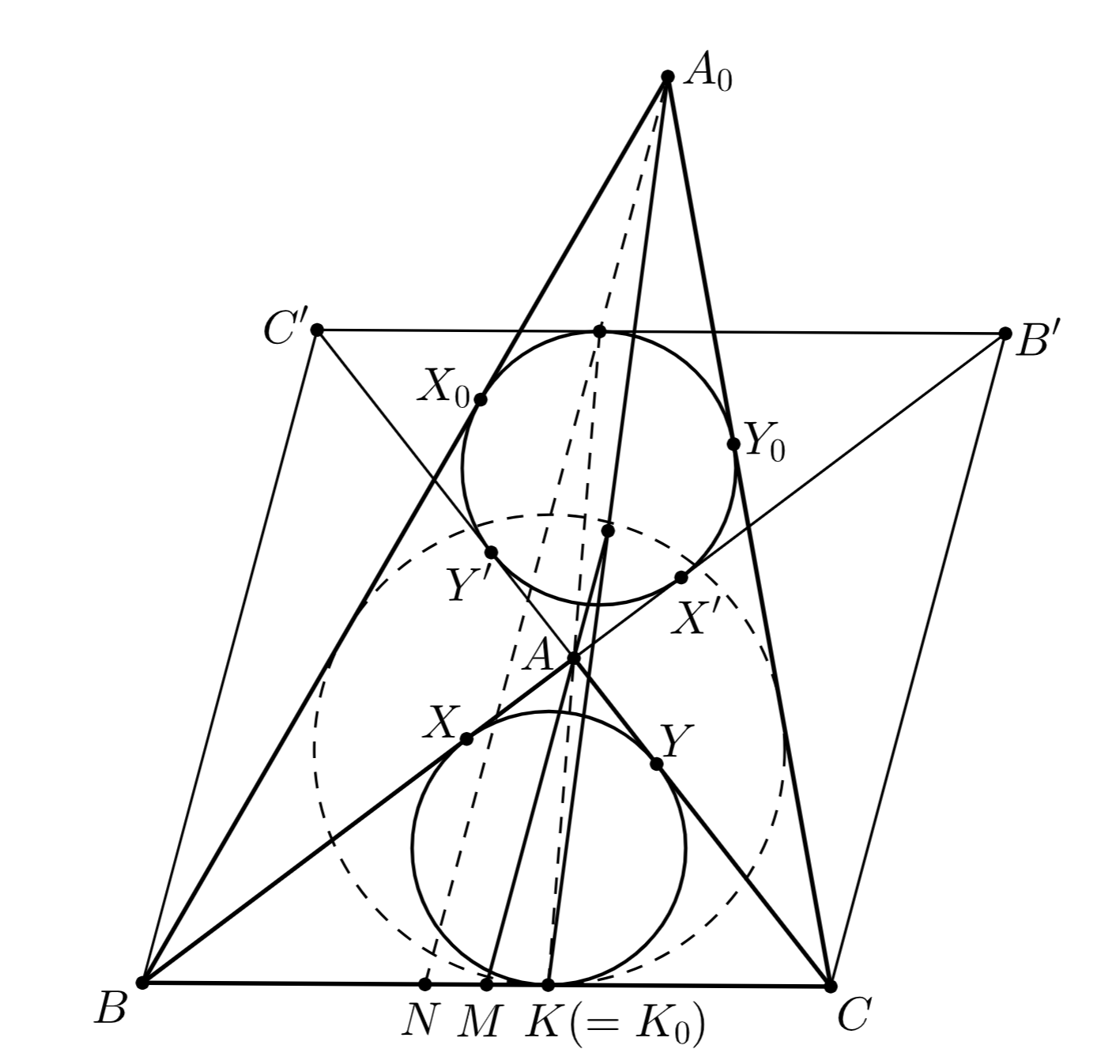
Пусть $ω$ касается $AB$ и $AC$ в точках $X$ и $Y$ соответственно, а $ω′$ касается отрезков $AB ′,$ $AC′,$ $A0B$ и $A0C$ в точках $X′,$ $Y ′,$ $X0$ и $Y0$ соответственно. Заметим, что

AB − AC = (AX + XB )− (AY + YC)= XB − YC =KB − KC.

Аналогично, если вписанная окружность треугольника $A0BC$ касается $BC$ в точке $K0,$ то

A0B− A0C =K0B − K0C.

Однако

A0B − A0C = (A0X0 + X0B)− (A0Y0+ Y0C)= X0B − Y0C =X ′B − Y′C = (XA + AB )− (YA +AC )= AB− AC,

так что $KB − KC =K0B − K0C,$ и потому $K = K0.$

Из доказанного следует, что вневписанные окружности треугольников $ABC$ и $A0BC$ также касаются отрезка $BC$ в одной и той же точке $N,$ симметричной $K$ относительно $M$ (поскольку $BN = CK$ ). Гомотетия с центром $A0,$ переводящая прямую $BC$ в прямую $B′C ′,$ переводит вневписанную окружность треугольника $A0BC$ в окружность $ω′,$ то есть точку $N$ — в $K ′.$ Значит, $N$ лежит на прямой $A0K;$ но, поскольку $BN = CK =C ′K ′,$ имеем $K ′N ∥B ′C,$ то есть $A0K ′ ∥B′C,$ что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание 1. После первого абзаца решение также можно завершить применением теоремы Брианшона к описанному (около $ω′$ ) шестиугольнику $A BB ′K ′C ′C. 0$ Теорема утверждает, что три главных диагонали $A K′, 0$ $BC ′,$ $B′C$ этого шестиугольника пересекаются в одной точке или попарно параллельны; в нашей задаче реализуется второй случай, то есть $′ ′ ′ A0K ∥BC ∥ B C.$

______________________________________________________________________________________________________________________________________________________

Замечание 2. Из утверждения задачи следует, что центр $′ I$ вписанной окружности треугольника $A0BC$ лежит на $AM.$ Существуют способы решить задачу, доказав этот факт.