Закл 2023

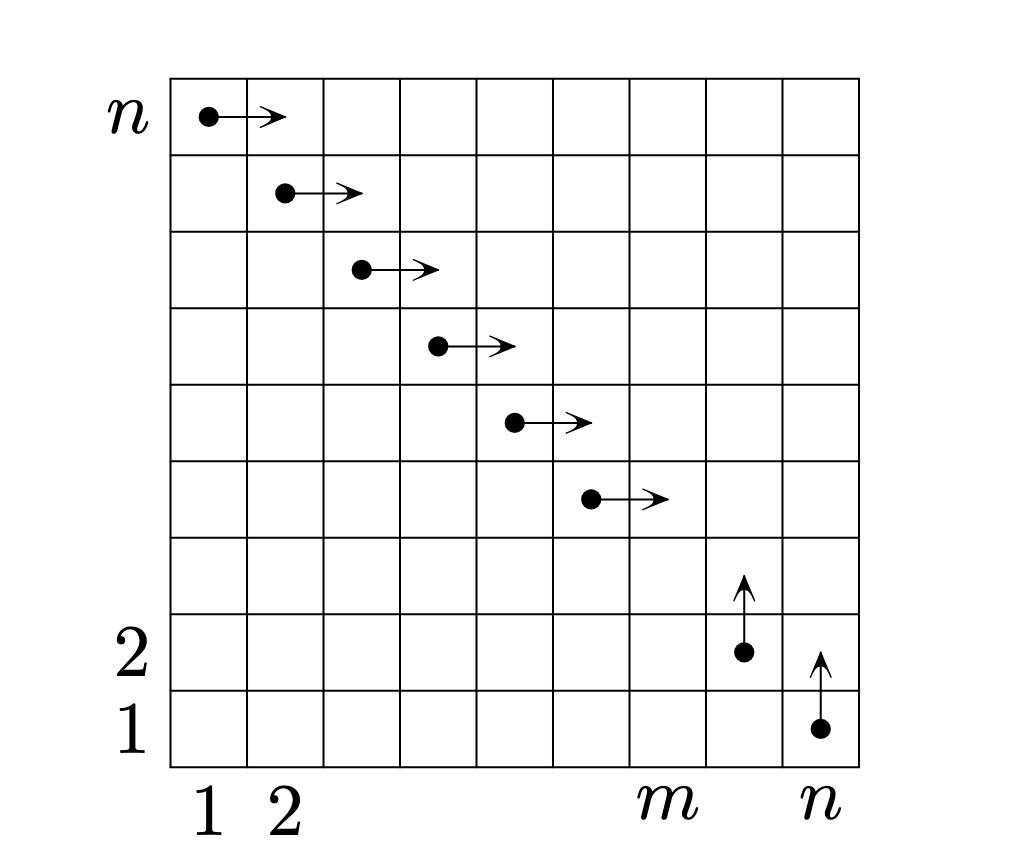
Будем изображать турнир в виде таблицы в которой и столбцы, и строки пронумерованы числами от до Столбцы будут соответствовать девочкам, а строки — мальчикам. Тогда каждая партия задаётся клеткой, координаты которой соответствуют номерам девочки и мальчика, играющих в этой партии. Поставим сначала фишку в клетку После победы девочки фишка будет перемещаться вверх, а в случае победы мальчика — вправо. При этом если фишка доходит до края таблицы, то из последней строки при движении вверх она перемещается в первую строку, а из последнего столбца при движении вправо — в первый столбец. Тогда условие задачи равносильно тому, что фишка обошла все клетки таблицы, побывав в каждой ровно по одному разу.

Раскрасим клетки таблицы в цветов по диагоналям, идущим вправо-вниз: первую диагональ — в первый цвет, вторую — во второй, -ю диагональ — в -й цвет, а следующие диагонали — снова в цвета с первого по -й. Заметим, что после каждой партии номер цвета клетки, в которой находится фишка, увеличивается на по модулю Так как всего в турнире было проведено партий, что кратно то в конце фишка находится в клетке -го цвета, то есть на главной диагонали (далее, говоря «диагональ», мы будем иметь в виду именно эту диагональ). Пусть финальная клетка в маршруте фишки расположена в столбце с номером тогда требуется доказать, что число нечётно.

Из верхней клетки диагонали фишка не могла пойти вверх, так как уже была в клетке Значит, если эта клетка не финальная, то из неё фишка пошла вправо. Тогда и из следующей клетки диагонали она сделала ход вправо, и т.д. до клетки, расположенной в столбце с номером Аналогично из клеток диагонали, находящихся в столбцах с номерами от до фишка ходила вверх. Пусть первая клетка диагонали, в которую попала фишка, находится в столбце с номером Рассмотрим путь фишки от начальной клетки до неё. Все пути от клеток первого цвета до следующей клетки -го цвета должны быть такими же, как и рассматриваемый путь, а именно, каждый такой путь получается из другого смещением на вектор Действительно, если бы фишка из клетки сделала ход вверх, а из клетки — вправо, то в клетку она бы не попала, а если из этих клеток она делала ходы вправо и вверх соответственно, то попала бы в одну клетку дважды; поэтому из каждых двух таких клеток фишка делала одинаковые ходы.

Без ограничения общности будем считать, что Клетки диагонали, находящиеся левее финальной клетки, будем называть левыми, а находящиеся правее — правыми. Пронумеруем левые клетки числами от до а правые — от до (и те, и другие нумеруем, двигаясь вправо-вниз). Посмотрим, в каком порядке фишка обходила эти клетки. С левых клеток она смещалась на клеток вправо (поскольку с них в клетку первого цвета она делала ход вправо), а с правых клеток — на клетку вправо. Значит, для левых клеток нам важен лишь остаток от деления номера на а для правых — от деления на При этом, если правых клеток меньше то можно увеличить на добавив правых клеток; это не повлияет на дальнейшие рассуждения. Для удобства заменим все номера клеток на соответствующие остатки, причём для правых клеток вместо остатка будем использовать число

Пусть число при делении на даёт остаток Тогда первый переход с левых клеток на правые был с числа на число и в этот момент все клетки с нулём в левой части были посещены. На диагонали остались только числа от до Дальше цепочка переходов между правыми и левыми клетками выглядит так:

В этой цепочке каждое число от до встречается два раза, начинается она на правых клетках, а заканчивается на левых. Переходы с правых клеток на левые будем называть переходами первого типа, а с левых на правые — второго. Тогда в цепочке переход первого типа и перехода второго, и они чередуются.

Докажем, что каждые два числа в цепочке, симметричные относительно её центра, дают в сумме Для крайних чисел это верно. Каждые два симметричных перехода имеют один тип, поэтому в них по модулю (для переходов первого типа) или по модулю (для переходов второго типа) прибавляется одно и то же число. Значит, сумма следующих двух симметричных чисел (которые ближе к центру цепочки) снова равна либо по модулю либо по модулю Но сумма самих чисел не меньше и не больше поэтому она может быть равна только

Предположим, что число чётно, и рассмотрим два случая.

1) Число нечётно. Тогда центральный переход в цепочке имеет второй тип. У правой нижней клетки диагонали нечётный номер, поскольку число нечётно, а чётно. Левая верхняя клетка диагонали тоже имеет нечётный номер, поэтому при переходе первого типа чётность числа меняется. Пусть с числа переход первого типа происходит на число Тогда по модулю переходы первого типа выглядят так: …, Суммы чисел в этих парах являются последовательными нечётными числами, поэтому при делении на они дают все нечётные остатки по два раза. В частности, есть переход, в котором сумма чисел равна по модулю Как показано выше, эта сумма равна Но тогда для этого перехода симметричный ему тоже имеет первый тип и содержит те же самые числа, то есть один из переходов повторился, чего быть не должно.

2) Число чётно. Тогда у центрального перехода в цепочке первый тип. Последняя левая клетка имеет нечётный номер, так как число нечётно, а чётно. У первой правой клетки тоже нечётный номер, значит, при переходе второго типа чётность числа не меняется. Аналогично первому случаю можно показать, что среди них найдётся переход, пара чисел в котором даёт сумму и получаем такое же противоречие.