Тема Закл (финал) 10 класс

Закл 2023

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#75128Максимум баллов за задание: 7

Даны натуральные числа $a$ и $b$ такие, что $a≥ 2b.$ Существует ли многочлен $P (x)$ степени больше $0$ с коэффициентами из множества ${0,1,2,...,b− 1}$ такой, что $P(a)$ делится на $P (b)?$

Источники: Всеросс., 2023, ЗЭ, 10.3(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Как известно, для целочисленного многочлена P выражение P(a) − P(b) кратно a − b. Если подобрать такой многочлен P, что P(b) = a − b, задача будет решена.

Подсказка 2:

Как насчёт того, чтобы рассмотреть a − b в системе счисления с основанием b?

Показать ответ и решение

Легко видеть, что если $b= 1,$ то всякий многочлен с коэффициентами от 0 до $b− 1$ является нулевым.

Пусть $b >1.$ Представим $a− b$ в $b$ -ичной записи (иными словами, в системе счисления с основанием $b$ ): $n a− b= cnb + ...+ c1b+ c0,$ где $ci ∈{0,1,2,...,b− 1}.$ Поскольку $a− b ≥b,$ в этой записи $n≥ 1.$

Покажем, что $n P (x)= cnx + ...+c1x+ c0$ удовлетворяет условию. Действительно, по теореме Безу, для любого многочлена $f$ с целыми коэффициентами $f(a)− f(b)$ делится на $a− b.$ Значит, $P (a)− P(b)$ делится на $a − b= P(b).$ Но тогда и $P (a)= (P (a)− P(b))+ P(b)$ делится на $P(b).$

Ответ:

Существует при $b> 1$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#90097Максимум баллов за задание: 7

У $100$ школьников есть стопка из $101$ карточки, которые пронумерованы числами от $0$ до $100.$ Первый школьник перемешивает стопку, затем берет сверху из получившейся стопки по одной карточке, и при каждом взятии карточки (в том числе при первом) записывает на доску среднее арифметическое чисел на всех взятых им на данный момент карточках. Так он записывает $100$ чисел, а когда в стопке остается одна карточка, он возвращает карточки в стопку, и далее все то же самое, начиная с перемешивания стопки, проделывает второй школьник, потом третий, и т.д. Докажите, что среди выписанных на доске $10000$ чисел найдутся два одинаковых.

Источники: ВСОШ, ЗЭ, 2023, 10.2 и 11.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Попробуйте посмотреть, какие множества чисел могут получаться у школьников на 1 шаге, на 2 шаге, на 100 шаге?

Подсказка 2

Попробуйте в явном виде найти все возможные значения, находящиеся в этих множествах. Как найти одинаковые среди них?

Подсказка 3

Рассмотрите первое, второе и сотое множества, а именно их объединение. Сколько в нëм чисел?

Показать доказательство

На $1$ -м шаге у каждого из $100$ человек было выписано одно из чисел множества

A1 = {0,1,2,...,100}

На $2$ -м шаге — одно из чисел множества

{ 1 2 3 199} A2 = 2,2,2,..., 2

На $100$ -м шаге выписано одно из чисел множества

{ S S− 1 S− 2 S− 100 } A100 = 100,-100-,-100-,...,-100--

где $S = 100-⋅101- 2$ — сумма всех чисел (а вычитается — число на оставшейся в конце карточке).

Видим, что ${ 1 2 3 199 200} A1 ∪A2 =A2 = 0,2,2,2,..., 2 , 2 ,$ так что $|A1∪ A2|= 201.$ Далее, $|A100|=101,$ но числа $1 1 50− 2,50,50+ 2$ принадлежат $A2∩A100,$ значит, $|A1 ∪A2∪ A100|≤ 201 +101− 3= 299.$

Итак, мы показали, что $300$ чисел, выписанных на $1$ -м, $2$ -м и $100$ -м шагах, могут принимать не более $299$ различных значений. Следовательно, какие-то два из них равны.

Ошибка.
Попробуйте повторить позже

Задача 3#107141Максимум баллов за задание: 7

Дано число $a ∈(0,1).$ Положительные числа $x , 0$ $x , 1$ $x, 2$ …, $x n$ удовлетворяют условиям

x0+ x1+...+xn = n +a

1-+ -1+ ...+ -1 =n + 1. x0 x1 xn a

Найдите наименьшее возможное значение выражения

2 2 2 x0+x1+ ...+ xn.

Источники: Всеросс., 2023, ЗЭ, 10.8(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Для начала попробуйте угадать ответ. Поможет его угадать условия на выражения. На самом деле достаточно найти самые тривиальные x_i для которых условие верно.

Подсказка 2

И правда ответ n + a². Теперь попробуйте переписать сумму квадратов x_i через сумму квадратов 1 - x_i для того, чтобы избавится от n в правой части.

Подсказка 3

Теперь нам достаточно доказать, что сумма квадратов (1 - x_i) больше, чем (1 - a)^2. Тут надо рассмотреть два случая. Попробуйте понять почему при x₀ ≤ a задача очевидна, где x₀ — минимальное из x_i.

Подсказка 4

Если же x₀ ≥ a, то попробуйте из каждого слагаемого вынести соответственное x_i и оценить его a.

Показать ответ и решение

Будем доказывать ответ $n+ a2.$ Заметим, что при $x =a 0$ и $x = x = ...= x = 1 1 2 n$ достигается равенство. Перепишем

∑ 2 ∑ 2 ∑ ∑ 2 xk = (1− xk) + 2 xk − (n+ 1)= (1 − xk) +n +2a− 1

Поэтому достаточно доказать, что

∑ 2 2 (1− xk) ≥(1− a)

Пусть $x0$ — наименьшее из чисел. При $x0 ≤ a$ имеем

∑ (1− xk)2 ≥ (1 − x0)2 ≥(1− a)2

Пусть $x0 ≥a,$ то

∑ ∑ ( 1 ) (1− x0)2 = xk x- − 2+ xk k

Так как $xk+ x1k ≥ 2,$ а значит, скобки из суммы неотрицательны. Следовательно,

∑ ( ) ∑ ( ) ( ) xk -1 − 2 +xk ≥a -1 − 2 +xk =a n+ 1− 2(n +1)+ n+ a = (1− a)2 xk xk a

Что и требовалось.

Ответ:

$n +a2$

Ошибка.
Попробуйте повторить позже

Задача 4#128454Максимум баллов за задание: 7

Квадрат $100×100$ разбит на квадраты $2× 2.$ Потом его разбивают на доминошки (прямоугольники $1 ×2$ и $2× 1).$ Какое наименьшее количество доминошек могло оказаться внутри квадратов разбиения?

Источники: ВСОШ, ЗЭ, 2023, 10.6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Нам необходимо сделать оценку снизу, то есть предъявить набор доминошек (возможно, просто доказать его существование), которые точно попадут в квадраты разбиения. Подумайте, как можно "ловить" подобные доминошки?

Подсказка 2:

Находить их в явном виде плохо, это просто не сделать (разбиений на домино очень много). Значит, нужно найти некоторые объекты, которые будут их "детектировать", то есть просто говорить, что они точно есть. Подумаем, какие самые тривиальные детекторы могут быть?

Подсказка 3:

Например, угловые клетки. В каждом углу доски нужная доминошка точно найдётся. Попробуем выделить несколько более высокоуровневые признаки. Почему доминошка, которая задевает угловую клетку, подходит?

Подсказка 4:

Потому что пересекает границу квадрата с нечётной стороной, а все такие границы лежать внутри квадратов разбиения, значит, такие доминошки всегда попадают в квадраты. Хм, что же хочется сделать?

Подсказка 5:

В такие моменты полезно попробовать обобщить идею! Как же будет звучать наше предположение?

Подсказка 6:

Для каждого квадрата с нечётной стороны, который исходит из левого нижнего угла, найдётся доминошка на его границе. Таким образом, мы сможем найти 50 нужных доминошек.

Подсказка 7:

Теперь нужно доказать, что для любого квадрата такая доминошка найдётся. Сделайте это самостоятельно, но скажем следующее: квадраты нечётные, а в доминошке ровно 2 клетки).

Подсказка 8:

Итого, мы нашли 50 требуемых доминошек. Кажется, можно найти больше...

Подсказка 9:

Осознайте, каким образом можно найти ещё 50 доминошек. Итого, есть оценка на 100 доминошек. Может, можно ещё больше?

Подсказка 10:

Спустя несколько попыток Вы, скорее всего, потерпели неудачу. Может, тогда пора переходить к примеру?

Подсказка 11:

Пример за Вами, однако скажем, что он достаточно "однородный"... Успехов!

Показать ответ и решение

Пример. Верхнюю и нижнюю горизонтали разобьём на горизонтальные доминошки — они окажутся в квадратах $2×2.$ Остальной прямоугольник $98× 100$ разобьём на вертикальные доминошки — они не окажутся в квадратах $2 ×2.$

Оценка. Рассмотрим квадраты $A1,$ $A3,...,A99$ размеров $1× 1,$ $3× 3,...,99× 99,$ у которых левый нижний угол совпадает с левым нижним углом исходного квадрата $100 ×100.$ Для каждого из квадратов $Ai$ $(i= 1,3,...,99)$ найдётся доминошка $Xi,$ пересекающая его сторону (поскольку квадраты нечётной площади не разбиваются на доминошки). Легко видеть, что $Xi$ лежит внутри квадратика $2× 2$ из разбиения. Аналогично, рассматривая квадраты $B1,B3,...,B99$ размеров $1×1,$ $3× 3,...,99× 99,$ у которых правый верхний угол совпадает с правым верхним углом исходного квадрата $100× 100,$ находим ещё $50$ нужных нам доминошек $Yj$ ( $j = 1,3,5,...,99).$ Это завершает решение (очевидно, что все доминошки $X1,$ $X3,...,X99,$ $Y1,$ $Y3,...,Y99$ различны).

Ответ:

100

Ошибка.
Попробуйте повторить позже

Задача 5#131940Максимум баллов за задание: 7

Прямые, содержащие стороны данного остроугольного треугольника $T,$ покрасили в красный, зелёный и синий цвета. Затем эти прямые повернули вокруг центра описанной окружности данного треугольника по часовой стрелке на угол $∘ 120$ (прямая сохраняет свой цвет после поворота). Докажите, что три точки пересечения одноцветных прямых являются вершинами треугольника, равного $T.$

Источники: ВСОШ, ЗЭ, 2023, 10.1 (см. olympiads.mccme.ru)

Показать доказательство

Пусть $ABC$ — данный треугольник, $O$ — центр его описанной окружности, $D,$ $E,$ $F$ — середины его сторон $BC,$ $CA,$ $AB$ соответственно, так что $DEF$ подобен $ABC$ с коэффициентом $1∕2$ и

OD ⊥ BC, OE ⊥CA, OF ⊥ AB.

Пусть при повороте вокруг $O$ по часовой стрелке на угол $120∘$ точка $D$ переходит в $D′.$ При таком повороте прямая $BC$ переходит в перпендикуляр к $OD′,$ проходящий через $D ′,$ пусть этот перпендикуляр пересекает $BC$ в точке $K.$

$PIC$

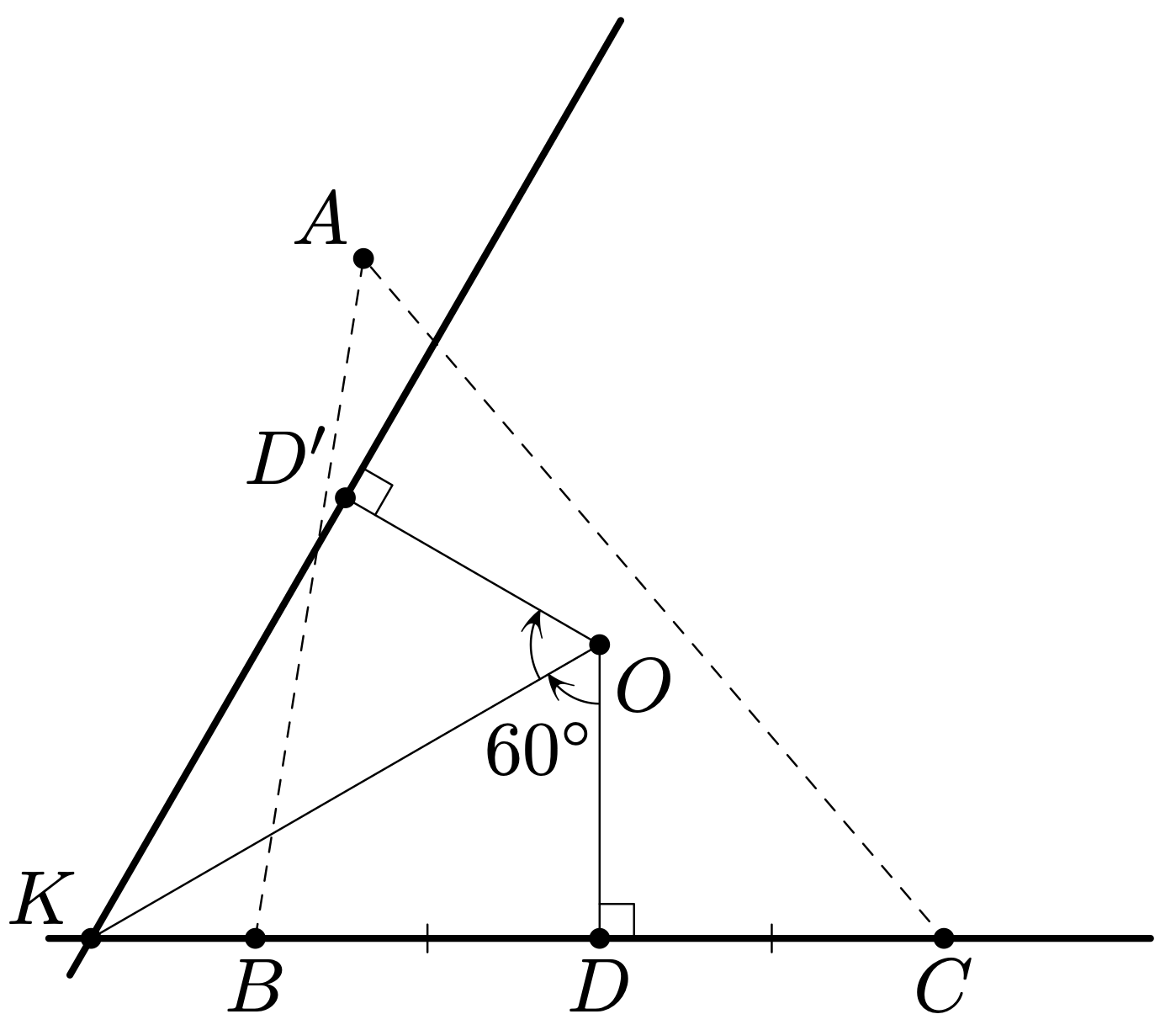
Видим, что прямоугольные треугольники $ODK$ и $OD ′K$ равны (симметричны относительно $OK$ ), и поэтому

′ ∠KOD = ∠DOD--= 60∘, 2

значит, в прямоугольном треугольнике $KOD$ верно $OK = 2OD.$

Иными словами, $K$ получается из $D$ в результате поворотной гомотетии: поворота с центром $O$ по часовой стрелке на угол $60∘$ и последующей гомотетии с центром $O$ и коэффициентом $2.$ Аналогичный результат получим для других точек $L,$ $M$ пересечения одноцветных прямых.

Таким образом, треугольник $KLM$ получается из $DEF$ поворотной гомотетией с центром $O$ и коэффициентом $2.$ Тогда $KLM$ подобен $DEF$ с коэффициентом $2,$ следовательно, равен $ABC.$

Ошибка.
Попробуйте повторить позже

Задача 6#131943Максимум баллов за задание: 7

С одной стороны теннисного стола выстроилась очередь из $n$ девочек, а с другой — из $n$ мальчиков. И девочки, и мальчики пронумерованы числами от 1 до $n$ в том порядке, как они стоят. Первую партию играют девочка и мальчик с номерами 1, а далее после каждой партии проигравший встаёт в конец своей очереди, а победивший играет со следующим. Через некоторое время оказалось, что каждая девочка сыграла ровно одну партию с каждым мальчиком. Докажите, что если $n$ нечётно, то в последней партии играли девочка и мальчик с нечётными номерами.

Источники: ВСОШ, ЗЭ, 2023, 10.4 (см. olympiads.mccme.ru)

Показать доказательство

Будем изображать турнир в виде таблицы $n×n,$ в которой и столбцы, и строки пронумерованы числами от $1$ до $n.$ Столбцы будут соответствовать девочкам, а строки — мальчикам. Тогда каждая партия задаётся клеткой, координаты которой соответствуют номерам девочки и мальчика, играющих в этой партии. Поставим сначала фишку в клетку $(1,1).$ После победы девочки фишка будет перемещаться вверх, а в случае победы мальчика — вправо. При этом если фишка доходит до края таблицы, то из последней строки при движении вверх она перемещается в первую строку, а из последнего столбца при движении вправо — в первый столбец. Тогда условие задачи равносильно тому, что фишка обошла все клетки таблицы, побывав в каждой ровно по одному разу.

Раскрасим клетки таблицы в $n$ цветов по диагоналям, идущим вправо-вниз: первую диагональ — в первый цвет, вторую — во второй, $...,$ $n$ -ю диагональ — в $n$ -й цвет, а следующие диагонали — снова в цвета с первого по $(n − 1)$ -й. Заметим, что после каждой партии номер цвета клетки, в которой находится фишка, увеличивается на $1$ по модулю $n.$ Так как всего в турнире было проведено $n2$ партий, что кратно $n,$ то в конце фишка находится в клетке $n$ -го цвета, то есть на главной диагонали (далее, говоря «диагональ», мы будем иметь в виду именно эту диагональ). Пусть финальная клетка в маршруте фишки расположена в столбце с номером $m,$ тогда требуется доказать, что число $m$ нечётно.

Из верхней клетки диагонали $n$ фишка не могла пойти вверх, так как уже была в клетке $(1,1).$ Значит, если эта клетка не финальная, то из неё фишка пошла вправо. Тогда и из следующей клетки диагонали она сделала ход вправо, и т.д. до клетки, расположенной в столбце с номером $m − 1.$ Аналогично из клеток диагонали, находящихся в столбцах с номерами от $m + 1$ до $n,$ фишка ходила вверх. Пусть первая клетка диагонали, в которую попала фишка, находится в столбце с номером $k.$ Рассмотрим путь фишки от начальной клетки до неё. Все пути от клеток первого цвета до следующей клетки $n$ -го цвета должны быть такими же, как и рассматриваемый путь, а именно, каждый такой путь получается из другого смещением на вектор $(1,−1).$ Действительно, если бы фишка из клетки $(a− 1,b)$ сделала ход вверх, а из клетки $(a,b− 1)$ — вправо, то в клетку $(a,b)$ она бы не попала, а если из этих клеток она делала ходы вправо и вверх соответственно, то попала бы в одну клетку дважды; поэтому из каждых двух таких клеток фишка делала одинаковые ходы.

$PIC$

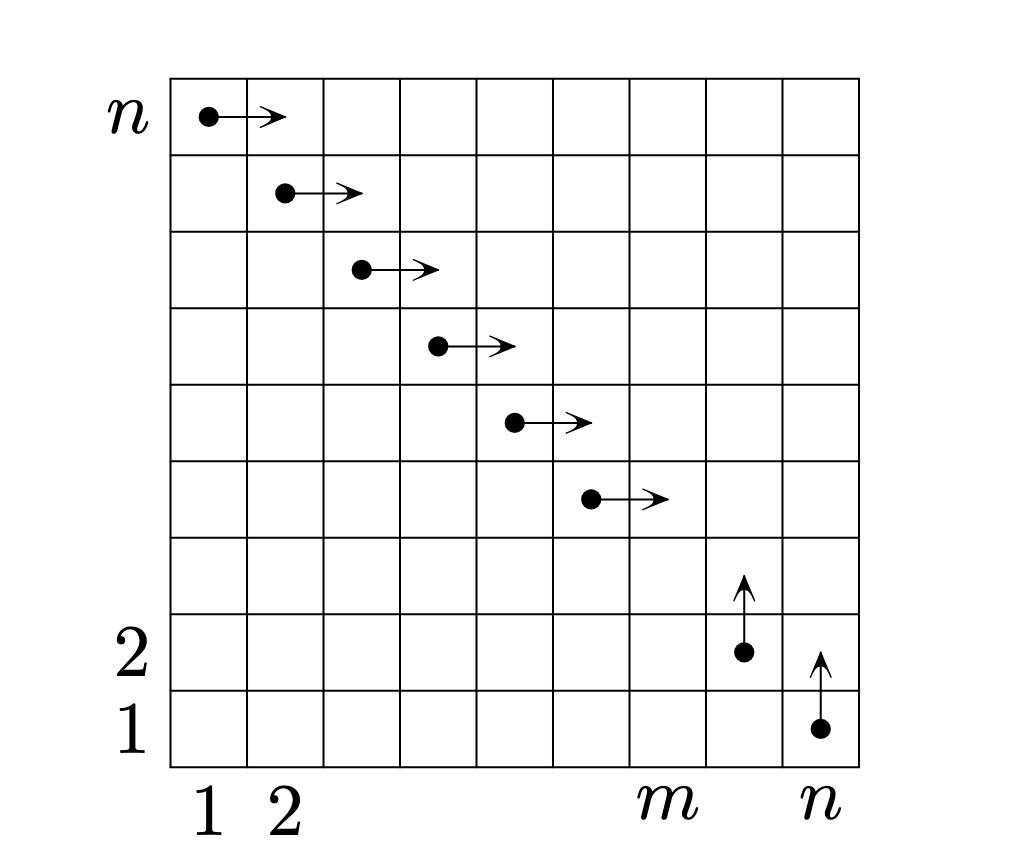
Без ограничения общности будем считать, что $k< m.$ Клетки диагонали, находящиеся левее финальной клетки, будем называть левыми, а находящиеся правее — правыми. Пронумеруем левые клетки числами от $1$ до $m − 1,$ а правые — от $1$ до $n− m$ (и те, и другие нумеруем, двигаясь вправо-вниз). Посмотрим, в каком порядке фишка обходила эти клетки. С левых клеток она смещалась на $k$ клеток вправо (поскольку с них в клетку первого цвета она делала ход вправо), а с правых клеток — на $k− 1$ клетку вправо. Значит, для левых клеток нам важен лишь остаток от деления номера на $k,$ а для правых — от деления на $k− 1.$ При этом, если правых клеток меньше $k,$ то можно увеличить $n$ на $2(k − 1),$ добавив $2(k − 1)$ правых клеток; это не повлияет на дальнейшие рассуждения. Для удобства заменим все номера клеток на соответствующие остатки, причём для правых клеток вместо остатка $0$ будем использовать число $k− 1.$

Пусть число $m$ при делении на $k$ даёт остаток $d.$ Тогда первый переход с левых клеток на правые был с числа $0$ на число $k− d,$ и в этот момент все клетки с нулём в левой части были посещены. На диагонали остались только числа от $1$ до $k− 1.$ Дальше цепочка переходов между правыми и левыми клетками выглядит так:

k− d → ⋅⋅⋅→ d.

В этой цепочке каждое число от $1$ до $k− 1$ встречается два раза, начинается она на правых клетках, а заканчивается на левых. Переходы с правых клеток на левые будем называть переходами первого типа, а с левых на правые — второго. Тогда в цепочке $k − 1$ переход первого типа и $k− 2$ перехода второго, и они чередуются.

Докажем, что каждые два числа в цепочке, симметричные относительно её центра, дают в сумме $k.$ Для крайних чисел это верно. Каждые два симметричных перехода имеют один тип, поэтому в них по модулю $k− 1$ (для переходов первого типа) или по модулю $k$ (для переходов второго типа) прибавляется одно и то же число. Значит, сумма следующих двух симметричных чисел (которые ближе к центру цепочки) снова равна либо $1$ по модулю $k− 1,$ либо $0$ по модулю $k.$ Но сумма самих чисел не меньше $2$ и не больше $2k− 2,$ поэтому она может быть равна только $k.$

Предположим, что число $m$ чётно, и рассмотрим два случая.

1) Число $k$ нечётно. Тогда центральный переход в цепочке имеет второй тип. У правой нижней клетки диагонали нечётный номер, поскольку число $n− m$ нечётно, а $k− 1$ чётно. Левая верхняя клетка диагонали тоже имеет нечётный номер, поэтому при переходе первого типа чётность числа меняется. Пусть с числа $1$ переход первого типа происходит на число $2s.$ Тогда по модулю $k− 1$ переходы первого типа выглядят так: $1→ 2s,$ $2 → 2s+1,$ …, $k− 1→ 2s+ k− 2.$ Суммы чисел в этих парах являются последовательными нечётными числами, поэтому при делении на $k− 1$ они дают все нечётные остатки по два раза. В частности, есть переход, в котором сумма чисел равна $1$ по модулю $k− 1.$ Как показано выше, эта сумма равна $k.$ Но тогда для этого перехода симметричный ему тоже имеет первый тип и содержит те же самые числа, то есть один из переходов повторился, чего быть не должно.

2) Число $k$ чётно. Тогда у центрального перехода в цепочке первый тип. Последняя левая клетка имеет нечётный номер, так как число $m − 1$ нечётно, а $k$ чётно. У первой правой клетки тоже нечётный номер, значит, при переходе второго типа чётность числа не меняется. Аналогично первому случаю можно показать, что среди них найдётся переход, пара чисел в котором даёт сумму $k,$ и получаем такое же противоречие.

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#131957Максимум баллов за задание: 7

Дана трапеция $ABCD,$ в которой $AD ∥BC,$ а лучи $AB$ и $DC$ пересекаются в точке $G.$ Общие внешние касательные к окружностям, описанным около треугольников $ABC$ и $ACD,$ пересекаются в точке $E.$ Общие внешние касательные к окружностям, описанным около треугольников $ABD$ и $BCD,$ пересекаются в точке $F.$ Докажите, что точки $E,F$ и $G$ лежат на одной прямой.

Источники: ВСОШ, ЗЭ, 2023, 9.7 и 10.7 (см. olympiads.mccme.ru)

Показать доказательство

Пусть прямая $EC$ повторно пересекает окружность $(ABC )$ в точке $X,$ а прямая $EA$ повторно пересекает окружность $(ACD )$ в точке $Y$ (мы разберём расположение точек, указанное на рисунке; другие случаи рассматриваются аналогично).

Рассмотрим гомотетию с центром $E,$ переводящую $(ABC)$ в $(ACD).$ При такой гомотетии точка $X$ переходит в $C,$ а точка $A$ — в $Y.$ Отсюда $AX ∥CY$ и

∠AEC = ∠AY C− ∠ECY = ∠AYC − ∠AXC.

Но $∠AXC =180∘− ∠ABC$ и $∠AY C = 180∘− ∠ADC.$ Значит,

∠AEC =∠ABC − ∠ADC =∠ABC − ∠BCG =∠BGC.

Из полученного равенства следует, что точки $A,$ $C,$ $E,$ $G$ лежат на одной окружности.

$PIC$

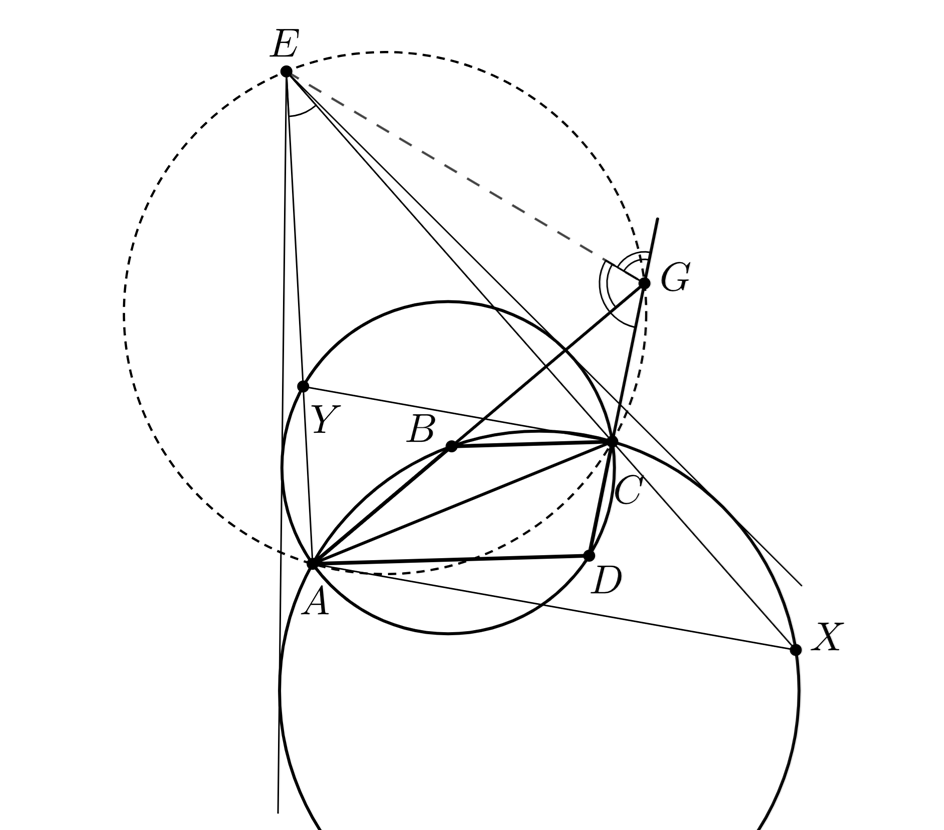
Поскольку точка $E$ лежит на серединном перпендикуляре к $AC$ (т.е. на оси симметрии окружностей $(ABC )$ и $(ACD )$ ), она является серединой дуги $AGC$ окружности $(ACEG ).$ Значит, $E$ лежит на внешней биссектрисе угла $BGC.$

Аналогично показывается, что $F$ также лежит на внешней биссектрисе угла $BGC.$

______________________________________________________________________________________________________________________________________________________

Замечание. У задачи есть следующее обобщение. Пусть $ABCD$ — четырёхугольник, $G =AB ∩ CD,$ а $M$ — вторая точка пересечения окружностей $(ADG )$ и $(BCG )$ (иначе говоря, точка Микеля этого четырёхугольника). Пусть $E$ — центр гомотетии с положительным коэффициентом, переводящей $(ABC )$ в $(ADC ).$ Тогда точки $A,$ $C,$ $M,$ $E$ лежат на одной окружности, причём $E$ — середина дуги $AC$ (т.е. $ME$ — биссектриса угла между $AM$ и $CM$ ).

Доказать это можно аналогично решению задачи: имеем (в направленных углах)

∠AEC = ∠ABC +∠ADC = ∠GBC +∠AMG = ∠GMC +∠AMG = ∠AMC.

Ошибка.
Попробуйте повторить позже

Задача 8#131959Максимум баллов за задание: 7

Найдите наибольшее натуральное число $n,$ для которого произведение чисел $n,n +1,$ $n +2,$ …, $n+ 20$ делится на квадрат какого-то одного из них.

Источники: ВСОШ, ЗЭ, 2023, 10.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать какой-нибудь пример. Чтобы легче придумывалось, попробуйте подобрать n так, чтобы произведение чисел от n до n + 20, делённое на n², равнялось некоторой цешке. Она целая.

Подсказка 2:

Попробуйте n = 20!. Чтобы показать, что при больших n это невозможно, предположите обратное. Пусть существует такое n и произведение делится на некоторое k². Рассмотрите частное произведения и k. Оно должно делиться на k. А с чем оно сравнимо по этому модулю?

Подсказка 3:

Пусть P = n(n + 1)...(n + 20), k = n + i, где i от 0 до 20. Тогда P / k = (k – i)(k – i + 1)...(k – 1)(k + 1)(k + 2)...(k + j), где j = 20 – i. Нетрудно видеть, что P / k сравнимо с (–1)ⁱi!j! по модулю k. Может ли (–1)ⁱi!j! делиться на k?

Подсказка 4:

Покажите, что число i!j! больше 0 и меньше 20!. Используйте для этого равенство j = 20 – i.

Показать ответ и решение

При $n= 20!$ имеем