Тема Закл (финал) 10 класс

Закл до 2015

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела закл (финал) 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 21#96593Максимум баллов за задание: 7

В остроугольном треугольнике $ABC$ на высоте $BK$ как на диаметре построена окружность $S,$ пересекающая стороны $AB$ и $BC$ в точках $E$ и $F$ соответственно. К окружности $S$ в точках $E$ и $F$ проведены касательные. Докажите, что их точка пересечения $P$ лежит на прямой, содержащей медиану треугольника $ABC,$ проведенную из вершины $B.$

Показать доказательство

$PIC$

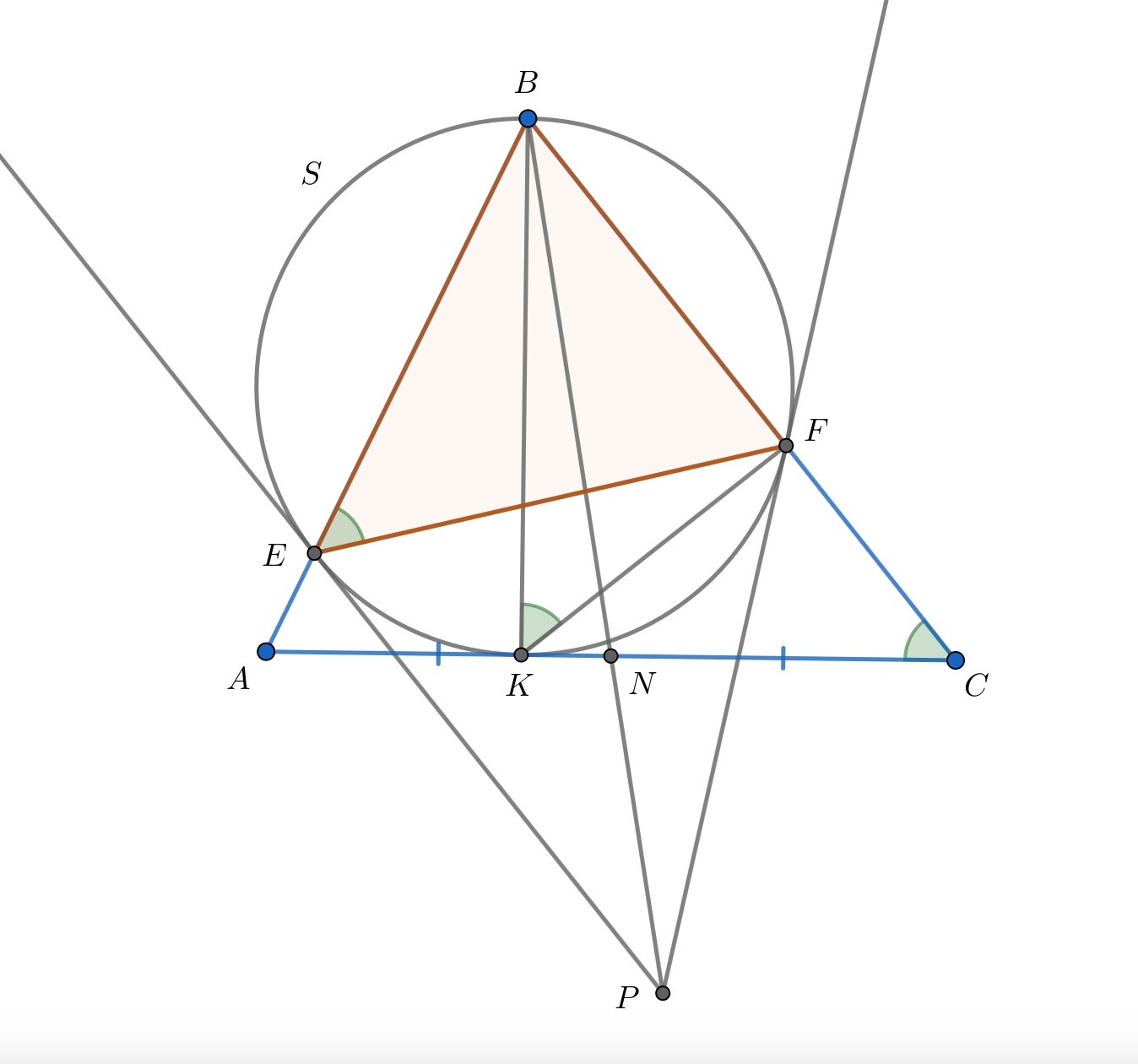
Заметнм, что $∠BEF = ∠BKF = ∠C$ (стороны последних двух углов взаимно перпендикулярны). Значит, треугольннк $FBE$ получается из треугольника $ABC$ симметрией относительно биссектрисы угла $B$ с последующей гомотетней с центром в точке $B$ . Следовательно, медиана $BN$ треугольника $ABC$ совпадает с симедианой треугольника $FBE$ . Но согласно основной задаче о симедиане эта симедиана проходит через указанную в условии точку пересечения касательных.