Регион 2023
Ошибка.
Попробуйте повторить позже
Дано натуральное число На клетчатой доске
расставили
ладей так, что никакие две не стоят в одной горизонтали или
одной вертикали. После этого доску разрезали по линиям сетки на две связных части, симметричных друг другу относительно центра
доски. Какое наибольшее количество ладей могло оказаться в одной из частей? (Клетчатая фигура называется связной,
если по этой фигуре от любой её клетки можно добраться до любой другой, переходя каждый раз в соседнюю по стороне
клетку.)
Источники:
Подсказка 1:
В подобных задачах часто ответ выражается через переменную и тривиальную константу (0, −1, +1). Навряд ли, ответ будет n + 7 или n + 5, но ничего нельзя говорить наверняка. Начнём с малого. Какую точно оценку мы можем гарантировать?
Подсказка 2:
n можно обеспечить при любом разбиении (банально взять ту часть, где больше). Тогда ответ, скорее всего, будет либо около n, либо около 2n (около — значит ±1 или 0). Если с этими вариантами потерпим крах, будем думать дальше. Итак, хочется проверить сначала более простые случаи. Какой же случай будет самым простым?
Подсказка 3:
Кажется, 2n, потому что чем больше ладей, тем проще получить противоречие. Но ещё не факт, что мы его получим. Попробуем сначала построить пример на 2n.
Подсказка 4:
Спустя несколько попыток вы поймёте, что это гиблый номер. Значит, хотим доказать, что 2n ладей не могут находиться в одной связной части. Вспомним условие на ладьи...
Подсказка 5:
Никакие две ладьи не стоят в одной вертикали или горизонтали. Осознайте, что в каждой вертикали и горизонтали есть ровно одна ладья. Какой тогда способ доказать, что в каждой части не более 2n − 1 ладьи, может оказаться рабочим?
Подсказка 6:
Доказать, что в каждой части есть целиком либо столбец, либо строка. Задача не самая простая. Какие строки и столбцы удобнее всего использовать?
Подсказка 7:
Крайние, ведь за ними следить явно проще, чем за теми, что в центре. А где крайние строки и столбцы, недалеко и до угловых клеток...
Подсказка 8:
С помощью них докажите, что в каждой части есть то, что нам нужно. Не забывайте, про центральную симметричность частей.
Подсказка 9:
Мы поняли, что ладей ≤ 2n − 1. Попробуем же теперь построить пример на 2n − 1...
Подсказка 10:
До него догадайтесь самостоятельно, но скажем одно: диагонали Вам в помощь! Успехов!
Заметим, что в каждой вертикали и каждой горизонтали стоит ровно по одной ладье.
Покажем сначала, что все ладей не могли попасть в одну часть. Пусть
— угловые клетки доски в порядке обхода
против часовой стрелки. Из симметрии,
и
должны принадлежать разным частям, как и
и
Это значит, что либо
и
либо
и
лежат в одной части, а остальные две клетки — в другой.
Пусть для определённости и
лежат в части I. Тогда все граничные клетки между ними также должны лежать в части I;
действительно, если какая-то такая клетка
лежит в части II, то в ней же лежит какой-то путь из
в
а в части I лежит какой-то
путь из
в
но эти пути должны иметь общую клетку, что невозможно.
Значит, вся горизонталь между клетками и
лежит в части I, то есть в ней должна быть хотя бы одна ладья. Аналогично, в части
II тоже есть целая горизонталь (между
и
), а значит, есть ладья. Отсюда и следует требуемое.
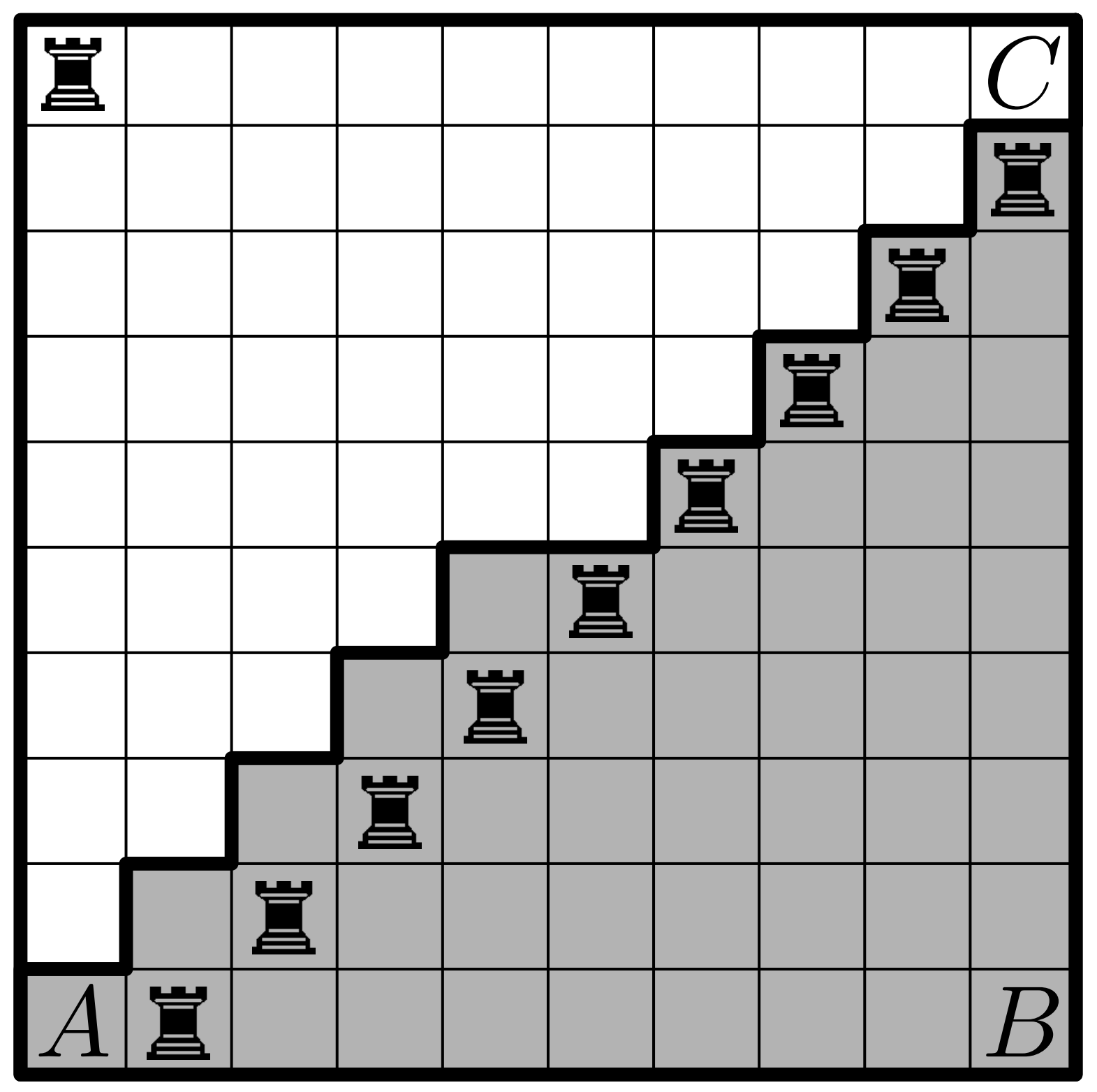
Осталось привести пример, когда в одной из частей расположено ладей. Один из возможных примеров устроен так. Рассмотрим
диагональ квадрата; в одну часть попадут клетки ниже нее, а также нижняя половина самой диагонали; остальные клетки
попадут во вторую часть. Расставим
ладью в клетки непосредственно под диагональю; тогда они окажутся в одной
части. Оставшуюся ладью поставим в пересечение оставшихся строки и столбца. На рисунке указан такой пример при
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




