Регион 2023
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Для натурального числа обозначим через
наименьшее общее кратное всех чисел
Существует ли такое натуральное
число
что
Источники:
Подсказка 1
Предположим, что это возможно и посмотрим на максимальную степень двойки, которую можно найти среди первых n+1 чисел. А что можно сказать о степени двойки, которую можно найти среди первых n чисел?
Подсказка 2
Верно! Если максимальная степень двойки среди первых n+1 чисел равна k, то среди первых n точно не меньше k/2. Какой вывод можно сделать?
Предположим, что такое существует. Пусть
делится на
но не делится на
Тогда
Значит, среди чисел
есть число
, делящееся на
Но тогда число
делится на
поэтому
делится на
Тогда, поскольку
то
делится на
что неверно.
Нет
Ошибка.
Попробуйте повторить позже
Велодорожка состоит из двух участков: сначала идёт асфальтовый, а затем песчаный. Петя и Вася стартовали порознь (сначала Петя, а затем Вася), и каждый проехал всю дорожку. Скорость каждого мальчика на каждом из двух участков была постоянной. Оказалось, что они поравнялись в середине асфальтового участка, а также в середине песчаного. Кто из мальчиков затратил на всю дорожку меньше времени?
Источники:
Подсказка 1:
Какую часть каждого из участков проехал каждый мальчик между моментами встречи?
Подсказка 2:
Они проехали по половине каждого из участков. Сколько времени затратил каждый из мальчиков на эти участки?
Первое решение. Между двумя моментами встречи каждый мальчик проехал половину асфальтового и половину песчаного участков, и они затратили на это поровну времени. Значит, на всю дорожку каждый из них затратил вдвое больше времени, то есть тоже поровну.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Нарисуем графики движения мальчиков по дорожке: на горизонтальной оси отмечаем время на вертикальной —
положение
мальчика, считая от начала дорожки.
Пусть
— точки, соответствующие старту Пети, моменту, когда он перешёл с асфальтового участка на песчаный, и его
финишу; пусть
— аналогичные точки для Васи. Тогда графики движения мальчиков — это ломанные
и
при
этом отрезки
и
горизонтальны (см. рисунок). По условию, середины отрезков
и
совпадают, откуда
— параллелограмм. Аналогично,
— параллелограмм. Значит, отрезки
и
параллельны и равны.
Поэтому между моментами финиша Пети и Васи прошло столько же времени, сколько и между моментами их старта; отсюда и следует
ответ.
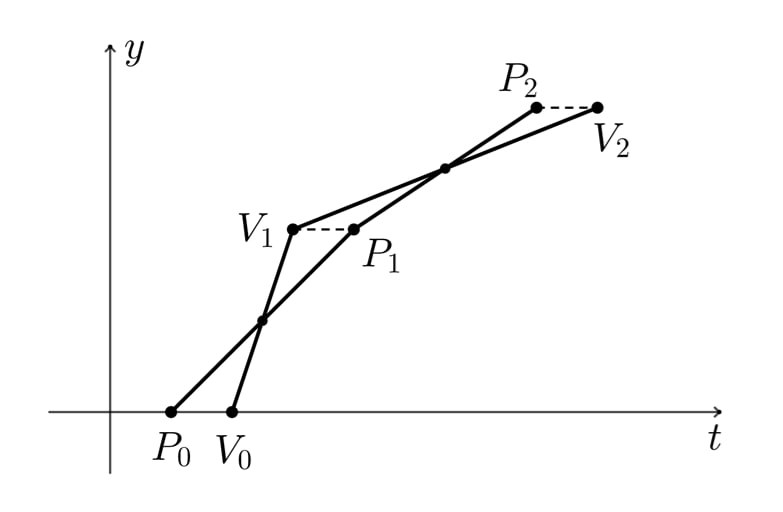
они затратили поровну времени
Ошибка.
Попробуйте повторить позже
Дан бумажный треугольник, длины сторон которого равны 5 см, 12 см и 13 см. Можно ли разрезать его на несколько (больше
одного) многоугольников, у каждого из которых площадь (измеренная в ) численно равна периметру (измеренному в
см)?
Источники:
Подсказка 1
Проверьте для исходного треугольника: чему равна его площадь? А его периметр?
Подсказка 2
Можно ли хороший многоугольник разрезать на несколько меньших хороших многоугольников?
Подсказка 3
Предположим, мы разрезали фигуру на несколько хороших многоугольников. Чему равна сумма площадей всех этих кусков? А теперь подумайте о сумме периметров всех кусков.
Многоугольник, у которого площадь (измеренная в ) численно равна периметру (измеренному в см), назовём хорошим.
Заметим, что исходный треугольник — хороший: он прямоугольный с катетами см и
см, поэтому его площадь равна
и
численно совпадает с его периметром, равным
Если какой-то многоугольник П разбит на хорошие многоугольники, то площадь П, равная сумме площадей всех многоугольников разбиения, совпала бы численно с суммой периметров многоугольников разбиения. Но сумма этих периметров больше периметра П (на удвоенную сумму длин общих частей границ многоугольников разбиения). Получаем, что площадь П больше его периметра.
Значит, никакой хороший многоугольник, в том числе данный треугольник, нельзя разрезать на несколько (больше одного) хороших многоугольников.
нельзя
Ошибка.
Попробуйте повторить позже
Дано натуральное число На клетчатой доске
расставили
ладей так, что никакие две не стоят в одной горизонтали или
одной вертикали. После этого доску разрезали по линиям сетки на две связных части, симметричных друг другу относительно центра
доски. Какое наибольшее количество ладей могло оказаться в одной из частей? (Клетчатая фигура называется связной,
если по этой фигуре от любой её клетки можно добраться до любой другой, переходя каждый раз в соседнюю по стороне
клетку.)
Источники:
Подсказка 1:
В подобных задачах часто ответ выражается через переменную и тривиальную константу (0, −1, +1). Навряд ли, ответ будет n + 7 или n + 5, но ничего нельзя говорить наверняка. Начнём с малого. Какую точно оценку мы можем гарантировать?
Подсказка 2:
n можно обеспечить при любом разбиении (банально взять ту часть, где больше). Тогда ответ, скорее всего, будет либо около n, либо около 2n (около — значит ±1 или 0). Если с этими вариантами потерпим крах, будем думать дальше. Итак, хочется проверить сначала более простые случаи. Какой же случай будет самым простым?
Подсказка 3:
Кажется, 2n, потому что чем больше ладей, тем проще получить противоречие. Но ещё не факт, что мы его получим. Попробуем сначала построить пример на 2n.
Подсказка 4:
Спустя несколько попыток вы поймёте, что это гиблый номер. Значит, хотим доказать, что 2n ладей не могут находиться в одной связной части. Вспомним условие на ладьи...
Подсказка 5:
Никакие две ладьи не стоят в одной вертикали или горизонтали. Осознайте, что в каждой вертикали и горизонтали есть ровно одна ладья. Какой тогда способ доказать, что в каждой части не более 2n − 1 ладьи, может оказаться рабочим?
Подсказка 6:
Доказать, что в каждой части есть целиком либо столбец, либо строка. Задача не самая простая. Какие строки и столбцы удобнее всего использовать?
Подсказка 7:
Крайние, ведь за ними следить явно проще, чем за теми, что в центре. А где крайние строки и столбцы, недалеко и до угловых клеток...
Подсказка 8:
С помощью них докажите, что в каждой части есть то, что нам нужно. Не забывайте, про центральную симметричность частей.
Подсказка 9:
Мы поняли, что ладей ≤ 2n − 1. Попробуем же теперь построить пример на 2n − 1...
Подсказка 10:
До него догадайтесь самостоятельно, но скажем одно: диагонали Вам в помощь! Успехов!
Заметим, что в каждой вертикали и каждой горизонтали стоит ровно по одной ладье.
Покажем сначала, что все ладей не могли попасть в одну часть. Пусть
— угловые клетки доски в порядке обхода
против часовой стрелки. Из симметрии,
и
должны принадлежать разным частям, как и
и
Это значит, что либо
и
либо
и
лежат в одной части, а остальные две клетки — в другой.
Пусть для определённости и
лежат в части I. Тогда все граничные клетки между ними также должны лежать в части I;
действительно, если какая-то такая клетка
лежит в части II, то в ней же лежит какой-то путь из
в
а в части I лежит какой-то
путь из
в
но эти пути должны иметь общую клетку, что невозможно.
Значит, вся горизонталь между клетками и
лежит в части I, то есть в ней должна быть хотя бы одна ладья. Аналогично, в части
II тоже есть целая горизонталь (между
и
), а значит, есть ладья. Отсюда и следует требуемое.
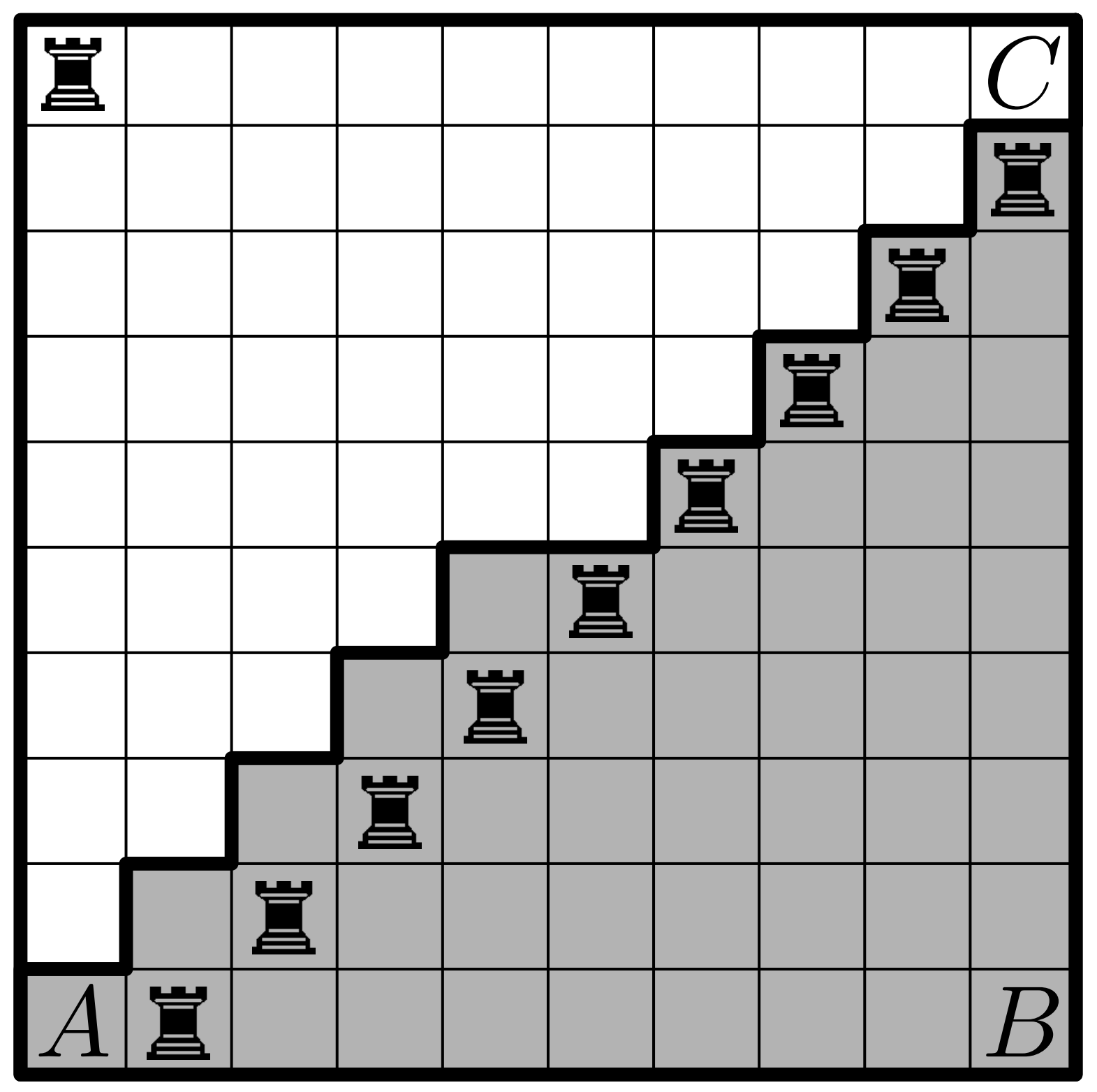
Осталось привести пример, когда в одной из частей расположено ладей. Один из возможных примеров устроен так. Рассмотрим
диагональ квадрата; в одну часть попадут клетки ниже нее, а также нижняя половина самой диагонали; остальные клетки
попадут во вторую часть. Расставим
ладью в клетки непосредственно под диагональю; тогда они окажутся в одной
части. Оставшуюся ладью поставим в пересечение оставшихся строки и столбца. На рисунке указан такой пример при
Ошибка.
Попробуйте повторить позже
Даны натуральные числа и
Ни одно из них не кратно другому. Известно, что число
делится на
Докажите, что
Источники:
Подсказка 1:
Будем доказывать от противного. Если дана делимость одного выражения на другое, то есть смысл рассмотреть какую-нибудь их линейную комбинацию.
Подсказка 2:
Рассмотрим разность abc + 1 и ab – b + 1, она равна b(ac – a + 1). Она тоже делится на ab – b + 1. Какие выводы можно сделать?
Подсказка 3:
Ясно, что b не имеет общих делителей с ab – b + 1. Значит, ac – a + 1 делится на ab – b + 1.
Подсказка 4:
Вспомним, что задача решается от противного, то есть предполагается, что b ≥ c + 1. Есть ощущение, что при таком раскладе ab – b + 1 редко когда меньше ac – a + 1.
Первое решение. Предположим противное: пусть Из делимости
на
следует, что число
кратно Поскольку числа
и
взаимно просты, получаем, что делится на
Ясно, что
поэтому либо
либо
В первом случае получаем
и, значит, делится на
что невозможно по условию. Во втором случае имеем
то есть
Это значит, что то есть
но это также невозможно по условию, ибо тогда снова
делится на
______________________________________________________________________________________________________________________________________________________
Второе решение. Опять же предположим противное. Поскольку делится на
то и
тоже кратно то есть
при некотором натуральном Иначе говоря,
Значит, делится на
По нашему предположению, С другой стороны, поскольку
имеем
откуда Значит,
и потому
Теперь переписывается в виде
то есть
Но тогда
то есть делится на
Это невозможно.
Ошибка.
Попробуйте повторить позже
Четырёхугольник вписан в окружность
Оказалось, что окружности, построенные на отрезках
и
как на диаметрах,
касаются друг друга внешним образом в точке
Пусть точки
и
— середины отрезков
и
соответственно.
Докажите, что перпендикуляр
к прямой
восстановленный в точке
пересекает прямую
в точке, лежащей на
Источники:
Обозначим окружности с диаметрами и
через
и
соответственно. Заметим, что точка
лежит на отрезке
Пусть прямые и
пересекают
в точках
и
соответственно. Поскольку
— диаметр
имеем
В прямоугольном треугольнике
отрезок
— высота, поэтому
С другой стороны, поскольку имеем
Итак,
то есть точки
и
лежат на одной окружности
.png)
Пусть теперь прямая пересекает окружности
и
в точках
и
соответственно (точка
лежит на отрезках
и
). Тогда
поскольку — центр окружности
С другой стороны,
что следует из того, что — высота в прямоугольном треугольнике
Значит,
то есть Но точка
отлична от
и
так как
не лежит на
значит, окружности
и
имеют три общих
точки
то есть они совпадают. Поэтому
лежит на
что и требовалось доказать.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание 1. Решение можно было бы завершить многими разными способами. Например, равенства
означают, что точки
и
лежат на одной окружности
Тогда либо окружности
и
совпадают, либо это
три разных окружности. Во втором случае радикальные оси пар этих трёх окружностей должны пересекаться в одной
точке или быть параллельными; но эти радикальные оси — это прямые
и
и для них эти утверждения
неверны.
Рассуждение выше имеет недостаток: оно не проходит, когда точки
и
лежат на одной прямой. Этот случай легко
разобрать отдельно (тогда
проходит через центр окружности
______________________________________________________________________________________________________________________________________________________
Замечание 2. Существуют и другие решения, идейно схожие с приведённым выше. Например, можно рассуждать так.
Пусть лучи и
пересекают
повторно в точках
и
Пусть
Тогда
откуда Тогда
— высота в прямоугольном треугольнике, и
С другой стороны, если прямая пересекает
в точках
и
то
Однако, как нетрудно проверить, на отрезке есть только две точки
такие, что
и это точки
и
Значит,
что и требовалось доказать.
.png)
Ошибка.
Попробуйте повторить позже
На доску записали 99 чисел, среди которых нет равных. В тетрадку выписали чисел — все разности двух чисел с доски (каждый раз
из большего числа вычитали меньшее). Оказалось, что в тетрадке число 1 записано ровно 85 раз. Пусть
— наибольшее число, записанное
в тетрадке. Найдите наименьшее возможное значение
Источники:
Подсказка 1:
Хорошей идеей будет разбить все числа на арифметические прогрессии с разностью 1.
Подсказка 2:
Попробуйте обозначить через nᵢ количество чисел в i-й прогрессии. Чему равна сумма всех nᵢ? Попробуйте вычислить количество прогрессий.
Подсказка 3:
Зная количество прогрессий и количество чисел, можно оценить количество чисел в какой-то из прогрессий с помощью принципа Дирихле. Дальше до оценки недалеко. Не забудьте про пример.
Докажем, что Все числа с доски разбиваются на цепочки чисел вида
так, что числа из разных цепочек не отличаются ровно на 1. Такое разбиение нетрудно построить, соединив любые два числа, отличающиеся на 1, отрезком и рассмотрев полученные ломаные.
Пусть получилось цепочек, в которых
…,
чисел соответственно (некоторые цепочки могут состоять из одного числа). В
цепочке из
чисел есть ровно
пара чисел, отличающихся на 1. Поэтому общее количество единиц в тетрадке
равно
откуда Значит, в одной из цепочек не меньше, чем
чисел, то есть не меньше 8 чисел. Разность наибольшего и
наименьшего чисел в такой цепочке не меньше
Осталось привести пример, в котором Такой пример дают, например, числа
Действительно, в этом примере и ровно для первых 85 из этих чисел в наборе есть число, на единицу большее.
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник в котором
Пусть
и
— середины сторон
и
соответственно, а
— основание высоты, опущенной из вершины
Вписанная окружность касается стороны
в точке
Прямая, проходящая через
и параллельная
пересекает отрезок
в точке
Докажите, что в четырехугольник
можно вписать
окружность.
Источники:
Первое решение. Совершим гомотетию с центром и коэффициентом
При этой гомотетии точки
и
переходят в
и
соответственно; пусть точки
и
переходят соответственно в
и
Тогда достаточно доказать, что четырёхугольник
описан. Мы докажем, что он описан около вписанной окружности
треугольника
Три стороны четырёхугольника уже касаются
поэтому достаточно доказать, что её касается
Пусть — центр
Тогда
поэтому
и
симметричны относительно
Далее заметим, что
Но — медиана в прямоугольном треугольнике
поэтому
Значит,
Значит, и прямые
и
также симметричны относительно
поскольку одна из них касается
то и другая тоже. Это и требовалось
доказать.
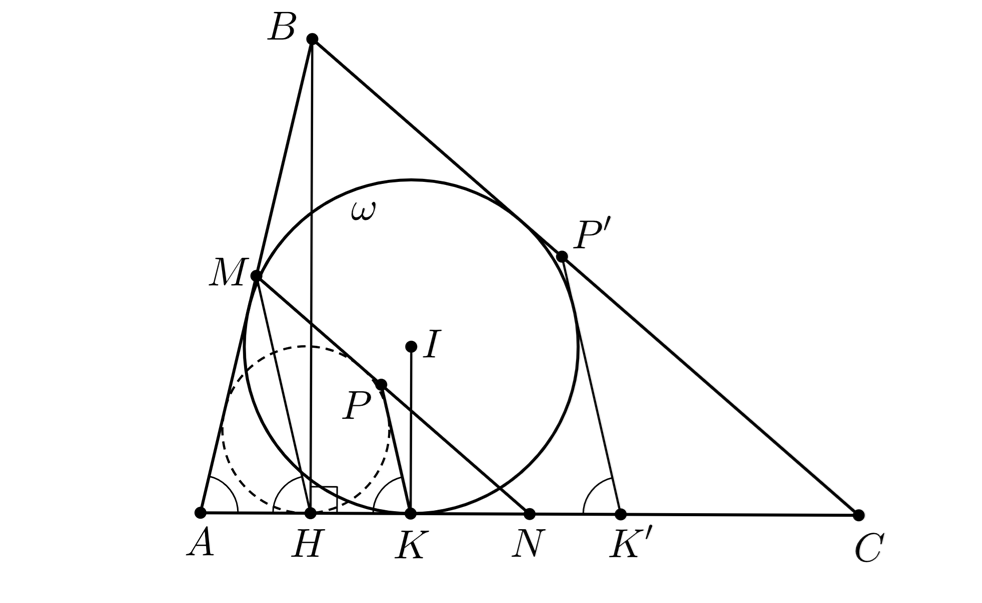
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. У решения выше есть несколько вариантов. Например, похожими рассуждениями можно показать, что в четырёхугольнике
биссектрисы трёх углов
и
проходят через одну точку — середину отрезка
Отсюда следует, что эта середина —
центр искомой вписанной окружности.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Пусть прямая пересекает прямую
в точке
Как и в решении выше, получаем, что
откуда
Мы докажем, что окружности, вписанные в треугольники и
совпадают (тогда это и будет вписанная окружность
четырёхугольника
). Поскольку обе окружности вписаны в угол
для этого достаточно показать, что они касаются
прямой
в одной и той же точке. Как известно, расстояния от
до точек касания этих окружностей с
равны
соответственно
Значит, нам надо доказать, что
или что
Обозначим полупериметр треугольника через
и пусть
Имеем
С другой стороны,
откуда и следует искомое равенство.
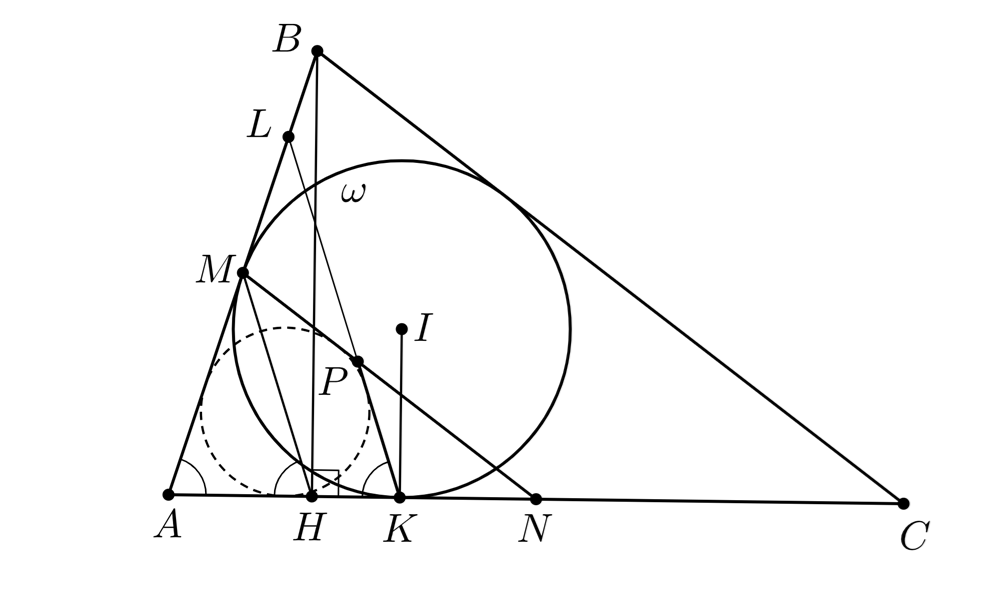
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Во втором абзаце решения по сути доказан следующий известный признак: четырёхугольник описан тогда и
только тогда, когда
(где
и
— точки пересечения продолжений боковых сторон, расположенные как на
рисунке).
Ошибка.
Попробуйте повторить позже
Найдите наибольшее число такое, что для любых положительных чисел
и
сумма которых равна 1, выполнено
неравенство
Источники:
Подсказка 1:
Попробуйте угадать максимальное m.
Подсказка 2:
Возьмите m = 1. Перед доказательством проделайте некоторые махинации со знаменателями, используя равенство a + b + c = 1.
Подсказка 3:
ab + c = ab + c(a + b + c) = (c + a)(c + b). Проделайте это со знаменателями. Далее сможете доказать вручную с помощью нескольких простых оценок.
Подсказка 4:
Осталось для m > 1 найти пример, при котором неравенство не выполнено. Пусть m = 1 + 2t, где t от 0 до 1 (если доказать это для 1 < m < 3, для других m это будет очевидно). Попробуйте как-нибудь грубо оценить каждое из слагаемых левой части сверху, чтобы из сумма получилась меньше 1 + 2t, то есть m.
Первое решение. Докажем сначала, что удовлетворяет требованиям задачи. Заметим, что
Следовательно,
Значит, осталось доказать неравенство
Возведем это неравенство в квадрат; оно примет вид
После сокращения слева останется сумма корней, а справа — Но любой из корней не меньше, чем
действительно,
например,
Отсюда и следует требуемое.
Осталось доказать, что при любом неравенство выполнено не всегда; достаточно это сделать при
Пусть
при
Положим
и
Тогда
однако
______________________________________________________________________________________________________________________________________________________
Второе решение. Приведём другое доказательство того, что подходит. Для этого докажем, что если
— наибольшее из чисел
то верно даже неравенство
Обозначим
заметим, что
поэтому
Левая часть неравенства выше переписывается
как
Значит, нам достаточно доказать, что
Возводя это неравенство в квадрат, получаем
после сокращения подобных слагаемых получаем, что нам достаточно доказать неравенство
Наконец, это неравенство вытекает из неравенства (поскольку
) и
где мы применили неравенство о средних.
Ошибка.
Попробуйте повторить позже
Куб разбит на миллион единичных кубиков; в каждом кубике расположена лампочка. Три грани большого куба,
имеющие общую вершину, окрашены: одна красным, другая синим, а третья зелёным. Назовём столбцом набор из 100
кубиков, образующих блок
У каждого из 30 000 столбцов есть одна окрашенная торцевая клетка; в этой клетке
стоит переключатель — нажатие на этот переключатель меняет состояние всех 100 лампочек в столбце (выключенная
лампочка включается, а включенная выключается). Изначально все лампочки были выключены. Петя нажал на несколько
переключателей, получив ситуацию, в которой ровно
лампочек горят. Докажите, что после этого Вася может нажать на
несколько переключателей так, чтобы ни одна лампочка не горела, использовав не более
переключателей с красной
грани.
Источники:
Ясно, что результат нажатия нескольких переключателей не зависит от того, в каком порядке эти нажатия были произведены — количество переключений каждой лампочки не зависит от этого порядка. В частности, можно считать, что Петя использовал каждый переключатель не более одного раза.
Весь куб разбивается на слоёв, параллельных красной грани. Каждый переключатель на некрасной грани переключает лампочки в
одном слое, а каждый переключатель на красной грани — по лампочке во всех
слоях.
После действий Пети найдётся слой, в котором включено лампочек — назовём один такой слой главным. Пусть
— набор из
переключателей на красной грани, связанных со включёнными лампочками в главном слое. Мы докажем, что Вася сможет погасить все
лампочки, использовав с красной грани ровно эти переключатели.
Запустим несколько другой процесс, начиная с того же исходного положения. Пусть — набор переключателей с красной грани,
использованных Петей, а
— набор использованных им переключателей с некрасных граней, связанных с главным слоем.
Пусть Петя применит
и
, а затем Вася применит
. После действий Пети в главном слое будут гореть те же
лампочек, что и раньше, а значит, после действий Васи все лампочки в главном слое будут погашены. Если теперь Вася
применит в каждом из остальных слоёв наборы переключателей с некрасных граней, аналогичные
, то все лампочки будут
погашены.
Пусть теперь Петя применит все остальные переключатели (с некрасных граней!), которые он применял исходно, а Вася
применит их ещё по разу. Все лампочки по-прежнему будут погашены. При этом в новом процессе Петя применил ровно те же
переключатели, что и в исходном, а Вася использовал лишь переключатели набора с красной грани (и какие-то — с
остальных граней). Значит, если в исходном процессе Вася совершит те же действия, которые он сделал в новом, он добьётся
требуемого.


