Тема Регион 10 класс

Регион 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#128694Максимум баллов за задание: 7

У Олега есть набор из 2024 различных клетчатых прямоугольников размеров $1× 1,$ $1 ×2,$ $1× 3,$ …, $1 ×2024$ (по одному прямоугольнику каждого размера). Может ли он, выбрав некоторые из них, составить какой-нибудь клетчатый квадрат площадью больше 1?

Источники: ВСОШ, РЭ, 2024, 9.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Предположим, что это возможно. Пусть n — наибольшая из длин выбранных прямоугольников. Попробуйте как-нибудь оценить площадь квадрата.

Подсказка 2:

Например, ясно, что его площадь не меньше n², поскольку сторона не меньше n. Возможно, можно найти какое-то противоречие с этим?

Подсказка 3:

Какой может быть наибольшая площадь выбранных прямоугольников?

Показать ответ и решение

Предположим противное, и пусть $n> 1$ — наибольшая из длин выбранных прямоугольников. Тогда составлен клетчатый квадрат $k× k,$ где $k≥ n >1.$ Значит, его площадь не менее $2 n .$ С другой стороны, его площадь не больше, чем суммарная площадь всех прямоугольников

1× 1, 1×2, ..., 1× n,

то есть не больше

n(n+-1)- 2 1 +2+ 3+ ⋅⋅⋅+ n= 2 <n .

Противоречие.

Ответ:

не сможет

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#128697Максимум баллов за задание: 7

В ряд выписаны по одному разу все натуральные числа от 1 до 1000 в каком-то порядке. Докажите, что можно выбрать несколько стоящих подряд выписанных чисел, сумма которых больше 100000, но не превосходит 100500.

Источники: ВСОШ, РЭ, 2024, 9.4 (см. olympiads.mccme.ru)

Показать доказательство

Среди наших чисел где-то есть $500.$ Покажем для начала, что можно выбрать числа с одной стороны от числа $500$ так, чтобы их сумма была больше 100000. Сумма всех без чисел без $500$ равна

1+1000 --2---⋅1000 − 500= 500000

Тогда по принципу Дирихле с одной из сторон от числа $500$ сумма чисел не меньше 250000. Тогда, очевидно, с одной стороны от числа $500$ можно выбрать несколько подряд идущих чисел так, чтобы их сумма превосходила 100000. Без ограничения общности будем полагать, что эти числа находятся справа от $500$ (то есть числа, общая сумма которых не меньше 250000). Обозначим эти числа $a1,$ $a2,$ …, $ak,$ где $a1$ — первое число справа от $500,$ $a2$ — второе число и так далее.

Выберем наименьшее такое $n,$ что

a1+ a2+ ...+an >100000.

Если теперь

a1+ a2+ ...+an ≤100500,

то мы уже нашли подходящие числа. Предположим, что это не так. Тогда $n$ — наименьшее такое число, что $a1+ a2+...+an >100500,$ поскольку

a1 +a2+ ...+ an− 1 ≤100000

в силу выбора $n.$ Покажем, что сумма

500+a1+ a2+ ...+an−1

подходит.

Во-первых, все слагаемые этой суммы в нашем ряду стоят подряд.

Во-вторых, $an ≤1000$ по условию. Обозначим

Si = a1+a2+ ...+ ai.

Тогда $Sn > 100500$ и, следовательно,

500+ Sn− 1 =500+ Sn− an > 500 +100500− 1000=100000.

Остается доказать, что эта сумма не превосходит $100500.$ Для этого используем знание о том, что $Sn−1 ≤ 100000.$ Тогда $500+ Sn−1 ≤ 100500.$

Ошибка.
Попробуйте повторить позже

Задача 3#128703Максимум баллов за задание: 7

На координатной плоскости нарисована парабола $y = x2.$ Для данного числа $k >0$ рассматриваются трапеции, вписанные в эту параболу (то есть все вершины трапеции лежат на параболе), у которых основания параллельны оси абсцисс, а произведение длин равно $k.$ Докажите, что продолжения боковых сторон всех таких трапеций проходят через одну точку.

Источники: ВСОШ, РЭ, 2024, 10.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте ввести координаты и написать уравнение боковой стороны AB. Если внимательно на него посмотреть, вы увидите эту точку.

Подсказка 2:

Пусть точки A и B имеют координаты (a, a²) и (b, b²). Тогда уравнение AB примет вид y = (a + b)x − ab. По всей видимости, мы хотим получить точку, у которой координаты будут выражаться через k.

Подсказка 3:

Обратите внимание на величину ab, она фиксирована и равна k²/4.

Показать доказательство

Пусть $ABCD$ — одна из рассматриваемых трапеций, $AD ∥ BC$ и $BC ∥Ox.$ Пусть точки $A$ и $B$ имеют координаты $(a,a2)$ и $(b,b2).$ Легко получить уравнение прямой $AB :$

2 2 2 2 (b − a )x− (b− a)y +(ba − ab )=0,

что после сокращения на $b− a ⁄=0$ превращается в

y = (a+ b)x− ab.

Но $ab$ равно произведению половин оснований трапеции. Отсюда $ab= k2. 4$ Следовательно, прямая $AB$ проходит через фиксированную точку $(0,− k2). 4$

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 4#128705Максимум баллов за задание: 7

По кругу стоят 100 белых точек. Аня и Боря красят по очереди по одной ещё не покрашенной точке в красный или синий цвет, начинает Аня. Аня хочет, чтобы в итоге оказалось как можно больше пар разноцветных соседних точек, а Боря — чтобы оказалось как можно меньше таких пар. Какое наибольшее число пар разноцветных соседних точек Аня может гарантировать себе независимо от игры Бори?

Источники: ВСОШ, РЭ, 2024, 10.3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте рассмотреть простую стратегию (она будет одинаковой для обоих игроков).

Подсказка 2:

Пусть Аня на каждом ходу ищет пару из неокрашенной и окрашенной точки, красит неокрашенную в противоположный цвет. Сколько пар она сможет создать?

Подсказка 3:

Учтите, что в конце игры количество разноцветных пар должно быть чётным. Почему это так?

Подсказка 4:

Стратегия Бори аналогична. Почему он не позволит Ане создать более 50 пар?

Показать ответ и решение

Нужно показать, что Аня всегда может добиться, чтобы разноцветных пар было не меньше 50, а Боря сможет помешать ей добиться, чтобы таких пар было больше 50.

Аня красит в любой цвет любую точку, а дальше каждым ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной (такая, очевидно, найдётся), и красит непокрашенную точку в цвет, отличный от цвета покрашенной. При этом образуется новая пара соседних разноцветных точек.

Боря каждым своим ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной, и красит непокрашенную точку в цвет, совпадающий с цветом покрашенной. При этом образуется новая пара соседних одноцветных точек.

Всего в круге имеется 100 пар соседних точек, и каждый игрок делает по 50 ходов. В итоге Боря добьётся того, что хотя бы 50 пар будут одноцветными, а Аня — что хотя бы 49 пар будут разноцветными. Однако количество разноцветных пар всегда чётно. Действительно, после окончания игры пройдём полный круг, начиная с какой-либо отмеченной точки (пусть для определённости с красной). Группы из идущих подряд красных и синих точек будут чередоваться: К—С—К—С—…—К, и значит, встретим пар разноцветных соседей вида К—С столько же, сколько пар вида С—К. Поэтому если пар разноцветных соседних точек не меньше 49, то их хотя бы 50.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 5#128708Максимум баллов за задание: 7

Диагонали выпуклого четырёхугольника $ABCD$ перпендикулярны и пересекаются в точке $O.$ Центры вписанных окружностей треугольников $ABC,$ $BCD,$ $CDA,$ $DAB$ являются вершинами выпуклого четырёхугольника, периметр которого равен $P.$ Докажите, что сумма радиусов вписанных окружностей треугольников $AOB,$ $BOC,$ $COD,$ $DOA$ не превосходит $P- 2.$

Источники: ВСОШ, РЭ, 2024, 10.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1.

В задаче надо сравнить два странных выражения. Давайте постепенно выражать их через более понятные отрезки. Начнём с суммы радиусов вписанных окружностей. Что можно заметить про треугольники, в которые вписаны наши окружности?

Подсказка 2.

Правильно! Они прямоугольные! Попробуйте вспомнить (или вывести), как выражается радиус вписанной окружности прямоугольного треугольника через его стороны.

Подсказка 3.

На самом деле радиус вписанной окружности треугольника AOB равен (OA + OB − AB)/2. Что получится, если сложить все четыре радиуса? Попробуйте выразить сумму только через отрезки, содержащие вершины четырёхугольника ABCD.

Подсказка 4.

Правильно! AC + BD - P/2, где P — периметр ABCD. Теперь хотелось бы получить похожее выражение для P. На самом деле отрезки между центрами вписанных окружностей посчитать хорошо, скорее всего, не получится, но можно оценить их длину снизу. Как это сделать?

Подсказка 5.

Стоит заметить, что у соседних вписанных окружностей есть общая касательная. Это может помочь в оценке?

Подсказка 6.

Да! На самом деле расстояние между центрами можно оценить через длину общей внешней касательной, которую уже несложно выразить через стороны исходного четырёхугольника ABCD. Попробуйте это сделать и сравнить с тем, что мы получили в сумме радиусов вписанных окружностей.

Показать доказательство

В прямоугольном треугольнике $AOB$ радиус вписанной окружности равен

1 2(OA + OB − AB )

(что также равно расстоянию от вершины прямого угла до точки касания катета со вписанной окружностью). Складывая это равенство с аналогичными для треугольников $BOC,$ $COD,$ $DOA,$ получаем, что сумма $S$ радиусов вписанных окружностей треугольников $AOB,$ $BOC,$ $COD,$ $DOA$ равна

1 P 2(2(OA +OB + OC +OD )− PABCD)= AC +BD − -ABC2D-.

$PIC$

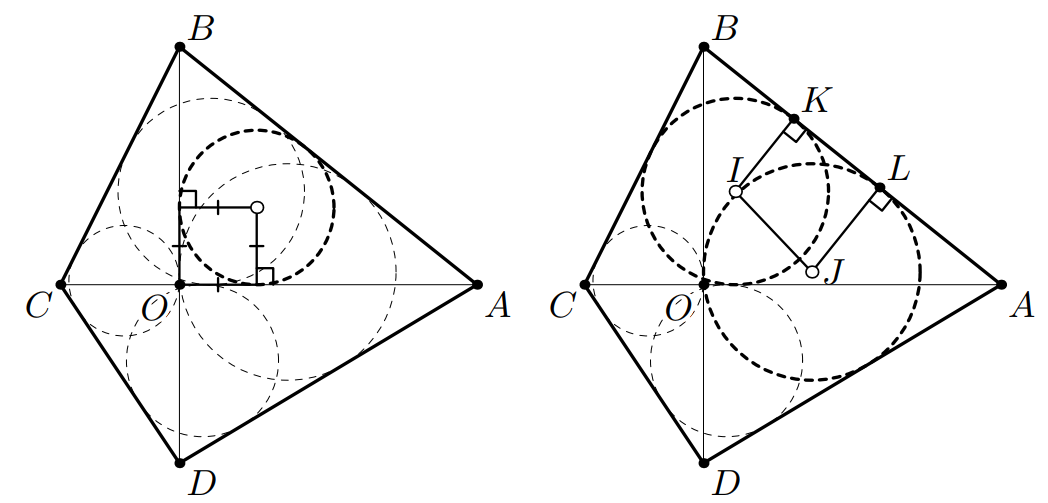
Пусть вписанные окружности треугольников $ABC$ и $DAB$ имеют центры $I,$ $J$ и касаются стороны $AB$ в точках $K$ и $L$ соответственно. Поскольку $KL$ — проекция $IJ$ на прямую $AB,$ имеем

1 1 IJ ≥ KL =AK − AL = 2(AC + AB − BC )− 2(AD + AB − BD )=

1 = 2(AC+ BD − BC − AD ).

Сложим это неравенство с аналогичными для расстояний между другими парами центров вписанных окружностей треугольников $ABC,$ $BCD,$ $CDA,$ $DAB.$ Получим оценку на периметр $P$ :

1 P ≥ 2(4AC +4BD − 2PABCD).

Сравнивая с выражением для $S,$ получаем требуемое неравенство $P ≥ 2S.$

Ошибка.
Попробуйте повторить позже

Задача 6#128938Максимум баллов за задание: 7

Сергей утверждает, что нашел различные вещественные числа $x,y,z$ такие, что

1 1 1 x2+-x+-1 + y2+-y+-1 + z2+-z+1-= 4.

Могут ли слова Сергея быть правдой?

Источники: ВСОШ, РЭ, 2024, 10.6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Получается, что нужно либо придумать пример, либо доказать, что равенства не может быть. Если верен второй случай, то, скорее всего, выражение слева будет либо всегда меньше 4, либо больше. Главный вопрос — насколько выражение слева удобно для оценивания?

Подсказка 2:

Оно вполне себе удобное, ведь в знаменателе каждой дроби находится простой квадратный трёхчлен, значение которого можно оценить снизу, а саму дробь, следовательно, сверху.

Показать ответ и решение

Заметим, что

2 2 2 4(x + x+ 1)=(4x +4x +1)+ 3= (2x+ 1)+ 3≥ 3,

причем равенство достигается только при $x = −1∕2.$ Тогда первое слагаемое

---1---- 4 x2+ x+ 1 ≤ 3

То же верно и для других слагаемых. Значит, левая часть уравнения Сергея не превышает $4∕3⋅3= 4,$ причем равенство достигается лишь при равенстве всех переменных $1 − 2,$ значит, равенство невозможно для различных $x,y,z.$

Ответ:

не могут

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#128940Максимум баллов за задание: 7

Петя утверждает, что он написал 10 подряд идущих натуральных чисел, и оказалось, что среди всех цифр, используемых в этих числах, каждая цифра (от 0 до 9) встречается одно и то же количество раз. Могли ли слова Пети оказаться правдой?

Источники: ВСОШ, РЭ, 2024, 10.7 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать пример с такими числами.

Подсказка 2:

Ясно, что последние цифры этих чисел в некотором порядке представляют собой набор цифр от 0 до 9. Значит, достаточно поработать с цифрами чисел, кроме последней.

Подсказка 3:

Если каждое число без последней цифры будет содержать одинаковое количество всех цифр, это даст требуемое.

Показать ответ и решение

Примером могут служить числа вида $A0,$ $A1,$ $A2,$ $A3,$ $A4,$ $A5,$ $A6,$ $A7,$ $A8,$ $A9,$ где в качестве $A$ можно взять любое число, состоящее из одинакового количества всех цифр от $0$ до $9,$ например, любую перестановку цифр $0,1,2,...,9,$ где $0$ не является первой цифрой.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. На самом деле, можно показать, что все возможные примеры устроены так. Заметим, что каждая из цифр $0,...,9$ появляется по разу в разряде единиц у рассматриваемых чисел. Предположим, что наименьшее из чисел на доске заканчивается не нулем, то есть происходит переход через разряд между числами, оканчивающимися на $0$ и $9.$

Рассмотрим последовательность из 10 подряд идущих натуральных чисел:

n, n+ 1, n+ 2, ..., n+ 9.

Предположим, что в этой последовательности происходит переход через степень $10$ (например, от $d 10 − 1$ к $d 10$ ). Иными словами, есть числа разной длины. Пусть числа от $n$ до $m$ имеют $d$ цифр, а числа от $m +1$ до $n+ 9$ – $d+ 1$ цифр, где $d m = 10 − 1.$ Тогда:

Количество чисел с $d$ цифрами: $m − n+ 1,$
Количество чисел с $d +1$ цифрами: $(n+ 9)− m.$

Так как всего 10 чисел:

(m − n +1)+ ((n+ 9)− m )= 10.

Общее количество цифр:

(10d− n)⋅d+ (n +10− 10d)⋅(d+1)= 10d+ n+10− 10d.

По условию, общее число цифр делится на $10$ (каждая из 10 цифр встречается одинаковое количество раз), получаем противоречие, ведь $n$ не делится на $10.$ Следовательно, переход невозможен, и все 10 чисел имеют одинаковое количество цифр $d.$

Рассмотрим число $[n-] C = 10 ,$ то есть все разряды исходного без единиц, количества вхождений цифр в эти разряды также равны между собой. Пусть оно имеет вид:

------- C = Ai9◟. ◝..◜9 ◞, k раз

где $i$ – это первая с конца цифра не равная 9, тогда

----------- C +1 =A (i+ 1)0◟.k.◝◜р.аз0◞,

Заметим, что в $A$ точно входит каждая цифра, отличная от $0,i,i+ 1,9,$ ведь иначе $i$ и $i+ 1$ имеют больше вхождений: в этом случае у них есть вхождение в некоторые числа не в разряде единиц, а другие его не имеют, поскольку второй переход через разряд в последовательности невозможен. Тогда для них общее количество вхождений в разряды за исключением единиц кратно $10,$ ведь $A$ не меняется при переходе через разряд. Тогда это верно и для всех цифр. Заметим, что среди $i,i+ 1$ есть хотя бы одно число не равное $0$ или $9,$ и количество его вхождений в разряды, кроме единиц, по модулю $10$ равно количеству чисел либо до перехода через разряд, либо после, то есть не равно $0,$ противоречие.

Цифра $j$ входит суммарно $10Cj +1$ раз, где $Cj$ — количество вхождений в запись $C,$ то есть в записи $C$ всех цифр поровну, тогда последовательность имеет требуемый вид:

------ --- C0,C1,...C9.

Ответ:

могли

Ошибка.
Попробуйте повторить позже

Задача 8#128943Максимум баллов за задание: 7

Дан четырёхугольник $ABCD,$ в котором $∠A = ∠C =90∘.$ Известно, что его вершины $A$ и $D$ вместе с серединами сторон $AB$ и $BC$ лежат на одной окружности. Докажите, что вершины $B$ и $C$ вместе с серединами сторон $AD$ и $DC$ тоже лежат на одной окружности.

Источники: ВСОШ, РЭ, 2024, 10.8 (см. olympiads.mccme.ru)

Показать доказательство

Первое решение. Обозначим через $K,L,$ $M,N$ середины сторон $AB,BC,$ $CD,DA$ соответственно. По условию, четырехугольник $AKLD$ — вписанный. Значит,

∘ ∘ ∠KLD =180 − ∠KAD = 90.

Поскольку $KL$ — средняя линия треугольника $ABC,$ то $KL ∥AC,$ поэтому $LD ⊥AC.$ Пусть отрезки $DL$ и $AC$ пересекаются в точке $D1.$

$PIC$

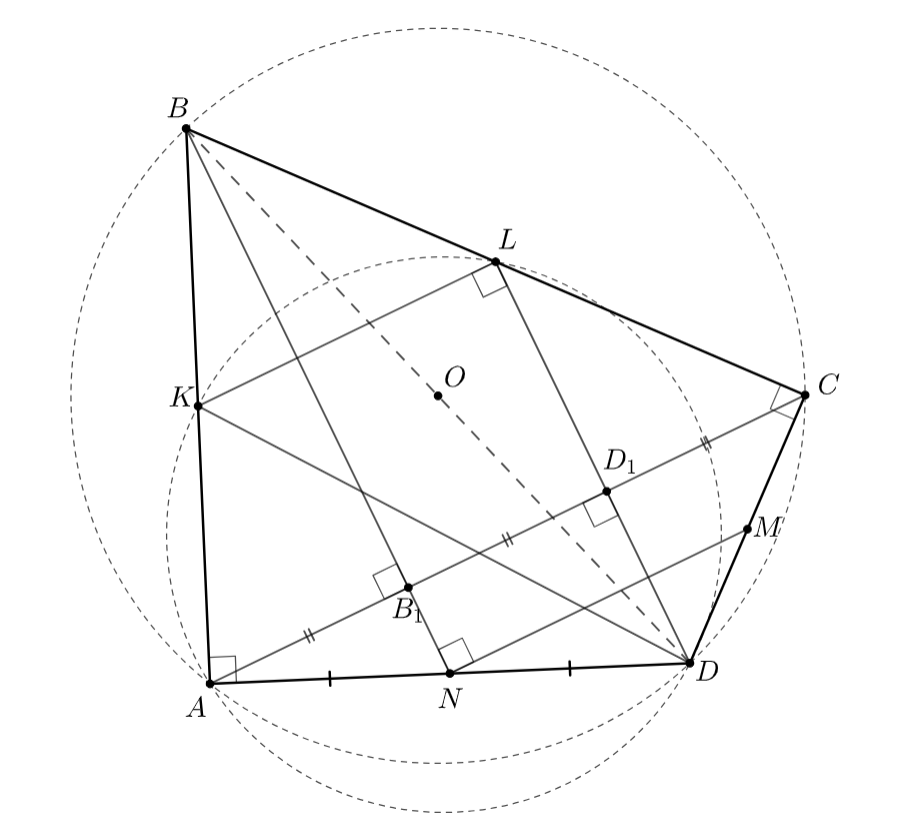
Опустим из точки $B$ перпендикуляр $BB1$ на прямую $AC.$ Тогда $BB1 ∥ LD1,$ значит, $D1$ — середина отрезка $CB1$ по теореме Фалеса. Кроме того, четырехугольник $ABCD$ вписан в окружность, построенную на отрезке $BD$ как на диаметре, обозначим центр этой окружности через $O.$ Вновь по теореме Фалеса проекции точек $B$ и $D$ на прямую $AC$ находятся на равном расстоянии от проекции точки $O,$ то есть от середины отрезка $AC.$ Из этого следует, что $CD1 = AB1.$ Итого,

AB1 =CD1 = BD1.

Значит, $B1N$ — средняя линия в треугольнике $AD1B,$ поэтому

B1N ∥DD1 и ∠D1B1N = 90∘.

Поскольку еще и $NM$ — средняя линия треугольника $ACD,$ то $∘ NM ∥AC и ∠B1NM = 90.$ Следовательно, точки $B,C,N$ и $M$ лежат на окружности с диаметром $BM,$ что и требовалось доказать.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Воспользуемся обозначениями из первого решения, $K,L,$ $M, N$ середины сторон $AB,BC,$ $CD,DA$ соответственно. Поскольку $KL$ — средняя линия треугольника $ABC,$ то $KL ∥AC.$ Отсюда и из вписанности четырехугольника $ABCD,$ мы получаем равенства углов:

∠BDC = ∠BAC = ∠BKL = 180∘− ∠AKL.

$PIC$

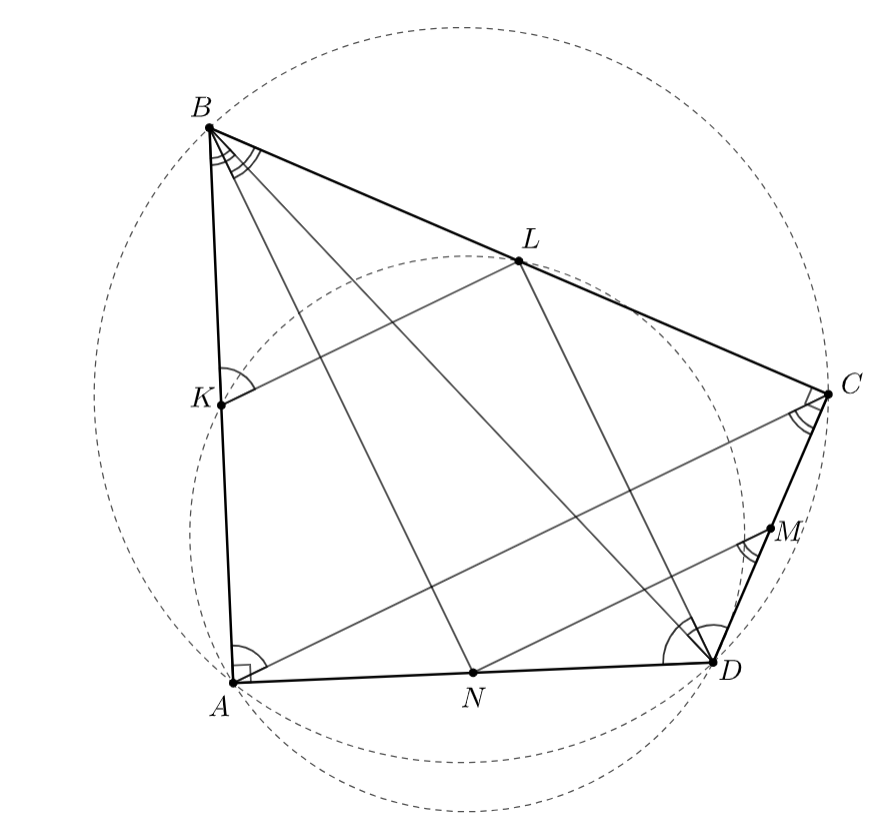
Таким образом, вписанность четырехугольника $AKLD$ равносильна равенству углов

∠ADL =∠BDC,

что эквивалентно равенству

∠ADB =∠CDL.

Последнее равенство равносильно подобию треугольников $LCD$ и $BAD,$ что эквивалентно равенству отношений их катетов

LC AB CD- = AD.

Домножая на знаменатели, получаем соотношение

AB ⋅CD = 1AD ⋅BC. 2

Рассуждая аналогично, получаем, что это же равенство равносильно вписанности четырехугольника $BNMC.$ Поскольку $MN$ — средняя линия треугольника $ABD,$ то $MN ∥ AC.$ Отсюда и из вписанности четырехугольника $ABCD,$ мы получаем равенства углов:

∠ABD = ∠ACD = ∠DMN = 180∘ − ∠CMN.

Таким образом, вписанность четырехугольника $BNMC$ равносильна равенству углов

∠CBN = ∠ABD

что эквивалентно равенству

∠ABN =∠CBD.

Последнее равенство равносильно подобию треугольников $BAN$ и $BCD,$ что эквивалентно равенству отношений их катетов

AN- AB- CD = BC.

Домножая на знаменатели, получаем соотношение

1 AB ⋅CD = 2AD ⋅BC,

что завершает данное доказательство.

Ошибка.
Попробуйте повторить позже

Задача 9#128947Максимум баллов за задание: 7

Найдите все тройки (не обязательно различных) натуральных чисел $a,b,c$ такие, что каждое из чисел $a+ bc,$ $b+ ca,$ $c+ab$ является простым делителем числа $2 2 2 (a +1)(b + 1)(c +1).$

Источники: ВСОШ, РЭ, 2024, 10.9 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Давайте сначала предположим, что все три числа различны. Может ли одна скобка делиться на два числа из этих трёх?

Подсказка 2:

Нет, ведь произведение любых двух чисел больше любой скобки. Докажите это. Значит, каждая скобка делится на какое-то из этих чисел. Давайте заметим, что условие задачи инвариантно относительно перестановки переменных. Поэтому давайте их упорядочим и рассмотрим наименьшую скобку. В каких случаях наименьшая скобка может делиться на какое-то из чисел?

Подсказка 3:

Пусть теперь какие-то из чисел совпали. В каком случае это возможно и как будет выглядеть условие?

Подсказка 4:

Итак, вы пришли к тому, что среди a, b, c точно есть единица. Пусть это c. Тогда 2(a² + 1)(b² + 1) должно делиться на простое число a + b. Обратите внимание на НОД скобочек.

Подсказка 5:

Итак, вы пришли к тому, что хотя бы два числа из a, b, c должны быть 1. Пусть это b и c. Тогда 4(a² + 1) должно делиться на a + 1. Посмотрите на НОД a² + 1 и a + 1.

Показать ответ и решение

Видим, что

a= b= c=1

удовлетворяет условию. Далее будет доказано, что других ответов нет.

1) Предположим, что

s= (a2+ 1)(b2+1)(c2+ 1)

делится на $pqr,$ где

p= a+ bc,q = b+ ca,r= c+ab

это следует из условия, если дополнительно предполагать, что $p,q,r$ различны.

Заметим, что один из трех сомножителей $a2+ 1,$ $b2+ 1,$ $c2 +1$ не может делиться на произведение двух из чисел $p,q,r,$ так как он меньше этого произведения. Действительно, рассмотрим, например, $pq.$ Из раскрытия скобок видим, что

pq > c2(ab)+ab≥ c2 +1, pq > b2c+ ab≥ b2+ 1

и аналогично

pq > a2+ 1.

Следовательно, каждый из сомножителей $a2+ 1,$ $b2+ 1,$ $c2+1$ должен делиться ровно на одно из чисел $p,q,r.$ Пусть, для определенности, $a$ — наименьшее из чисел $a,b,c.$ Тогда $a2 ≤ bc$ и $1≤ a,$ поэтому $a2 +1$ может делиться на $p= bc +a$ только в случае $a2 = bc$ и $a = 1,$ т.е в случае

a = b=c =1.

Далее, $2 a ≤ ac$ и $1≤ b,$ поэтому $2 a +1$ может делиться на $q = ac+ b$ только в случае $2 a = ac$ и $b= 1,$ т.е в случае

a = b=c =1.

Аналогично, $a2+ 1$ может делиться на $r= ab+c$ только при

a = b=c =1.

2) Пусть какие-то два из трех чисел $p,q,r$ совпадают, скажем, $p =q.$ Тогда

0= q− p= b+ca− a− bc= (a− b)(c− 1).

Значит, либо $a= b,$ либо $c= 1.$ Первый случай возможен лишь при $a= b=1,$ иначе

p= a+bc= a+ ac= a(a+ c)

— составное число, что дает противоречие. Значит, в любом случае среди $a,b,c$ присутствует единица, скажем, $c= 1.$

Тогда наши данные простые числа — это $p= a+ b,$ $q = a+ b$ и $r= ab+ 1,$ и они должны быть делителями

s= 2(a2+ 1)(b2+1).

Если хотя бы одно из чисел $a,b$ больше 1, то $p> 2$ и на $p= a+b$ обязан делиться хотя бы один из сомножителей $a2+1$ и $b2+ 1.$ А поскольку разность

(a2 +1)− (b2+ 1)=(a− b)(a+ b)

делится на $p= a+ b,$ получаем, что оба числа $a2+1,$ $b2+ 1$ делятся на $p.$ Тогда если $r$ отлично от $p= q,$ то $s$ делится на $pqr,$ что разобрано в случае $1.$

Остается вариант

p= q = r.

Рассуждаем как в предыдущем случае и получаем, что хотя бы два из трех чисел $a,b,c$ обязаны равняться $1.$ Пусть, например,

a =b =1,p= q = r= c+1,s= 4(c2+ 1).

Случай $c=1$ уже был ранее. Если $c> 1,$ то $c+ 1$ — нечетное простое, значит $c2+1$ должно делиться на $c+ 1.$ Отсюда

(c2+ 1)− (c+1)= c(c− 1)

должно делиться на $c+ 1.$ Но это невозможно, так как

0< c− 1< c<c +1

и $c+ 1$ — простое.

Ответ:

$(1,1,1)$

Ошибка.
Попробуйте повторить позже

Задача 10#128949Максимум баллов за задание: 7

Каждый из 2024 людей является рыцарем или лжецом. Некоторые из них дружат друг с другом, причём дружба взаимна. Каждого из них спросили про количество друзей, и все ответы оказались различными целыми числами от 0 до 2023. Известно, что все рыцари отвечали на вопрос верно, а все лжецы изменяли истинный ответ ровно на 1. Какое наименьшее число лжецов могло быть среди этих людей?

Источники: ВСОШ, РЭ, 2024, 10.10 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Рассмотрим разбиение людей на две группы, группа A: назвали числа от 0 до n−1, группа B: назвали числа от n до 2n−1, где n = 1012. Можно ли связать число дружб людей из разных групп, обозначим его E, с числом лжецов в A/B?

Подсказка 2

Е оценивается сверху через истинное число друзей персонажей из A, а его можно оценить сверху через число лжецов в A. Есть ли аналогичная оценка для E снизу через число лжецов в B?

Подсказка 3

Почти все дружелюбные люди из группы B дружат более чем с половиной рыцарей и лжецов, значит, и с кем-то из A. Как для отдельного человека оценить это количество?

Подсказка 4

Сравним оценки для E: n(n−1)/2 + x ≥ E ≥ n(n+1)/2 − y, где x, y — количество лжецов в A и В соответственно. Какой отсюда следует вывод об общем числе лжецов?

Подсказка 5

x + y ≥ n. Надо построить пример с n лжецами. Может рассмотреть крайний случай, где достигаются оценки или где все лжецы входят в одну группу?

Показать ответ и решение

Оценка. Пусть $n= 1012.$ Людей обозначим вершинами, номер вершины будет означать ответ соответствующего человека, а если пара людей дружит, то проведем ребро между соответствующими вершинами.

Пусть $A$ — множество всех людей, которые назвали числа от 0 до $n− 1,$ а $B$ — множество всех людей, которые назвали числа от $n$ до $2n − 1.$ Пусть $di$ — степень вершины $i.$ Тогда по условию $di = i,$ если $i$ — рыцарь, и $|di− i|= 1$ в противном случае. Пусть в множестве $A$ ровно $x$ лжецов, а в множестве $B$ — ровно $y.$

Оценим количество $E$ ребер между людьми из разных множеств $A$ и $B.$

С одной стороны, $E$ не больше суммы степеней вершин множества $A,$ откуда

(n− 1)n E ≤ d0+d1+ ...+ dn−1 ≤0 +1+ 2+ ...+ (n − 1)+ x=--2---+x.

С другой стороны, из каждой вершины $i$ множества $B$ не более $n− 1$ ребер идет в вершины множества $B,$ и значит, не менее $di− (n − 1)$ ребер идет в вершины множества $A.$ Отсюда

E ≥ dn+ dn+1+...+d2n−1− n(n − 1)≥ n+ (n +1)+ ...+ (2n− 1)− y − n(n− 1)

n(n +1) = --2---− y.

Получаем неравенство:

n(n+-1)- (n−-1)n 2 − y ≤ 2 + x,

откуда $x+ y ≥ n.$ Это означает, что всего лжецов не менее $n.$

Пример. Как и прежде, номер человека будет означать его ответ. Возьмем два множества людей:

C = {0,1,...,n − 1}

D ={n,n+ 1,...,2n− 1}.

Пусть в множестве $C$ никакие двое людей не дружат друг с другом, а в множестве $D$ — любые двое дружат. Далее, пусть человек $i∈C$ и $j ∈ D$ дружат тогда и только тогда, когда $i+ j ≥2n − 1.$ Тогда у человека $i∈ C$ всего $i+1$ друг:

2n− 1,2n− 2,...,2n − i− 1.

У человека $j ∈D$ будет всего $j$ друзей:

это j− n+ 1 людей n − 1,n− 2,...,2n− j− 1

из множества $C$ и все люди множества $D,$ кроме него самого. При этом все люди в $C$ — лжецы, а в $D$ — рыцари. Видим, что все условия задачи выполняются.

Ответ:

1012