Регион 2022
Ошибка.
Попробуйте повторить позже
На стороне остроугольного треугольника
отмечены точки
и
так, что
На дуге
описанной окружности
треугольника
не содержащей точку
нашлись такие точки
и
что
и
Докажите, что
Источники:
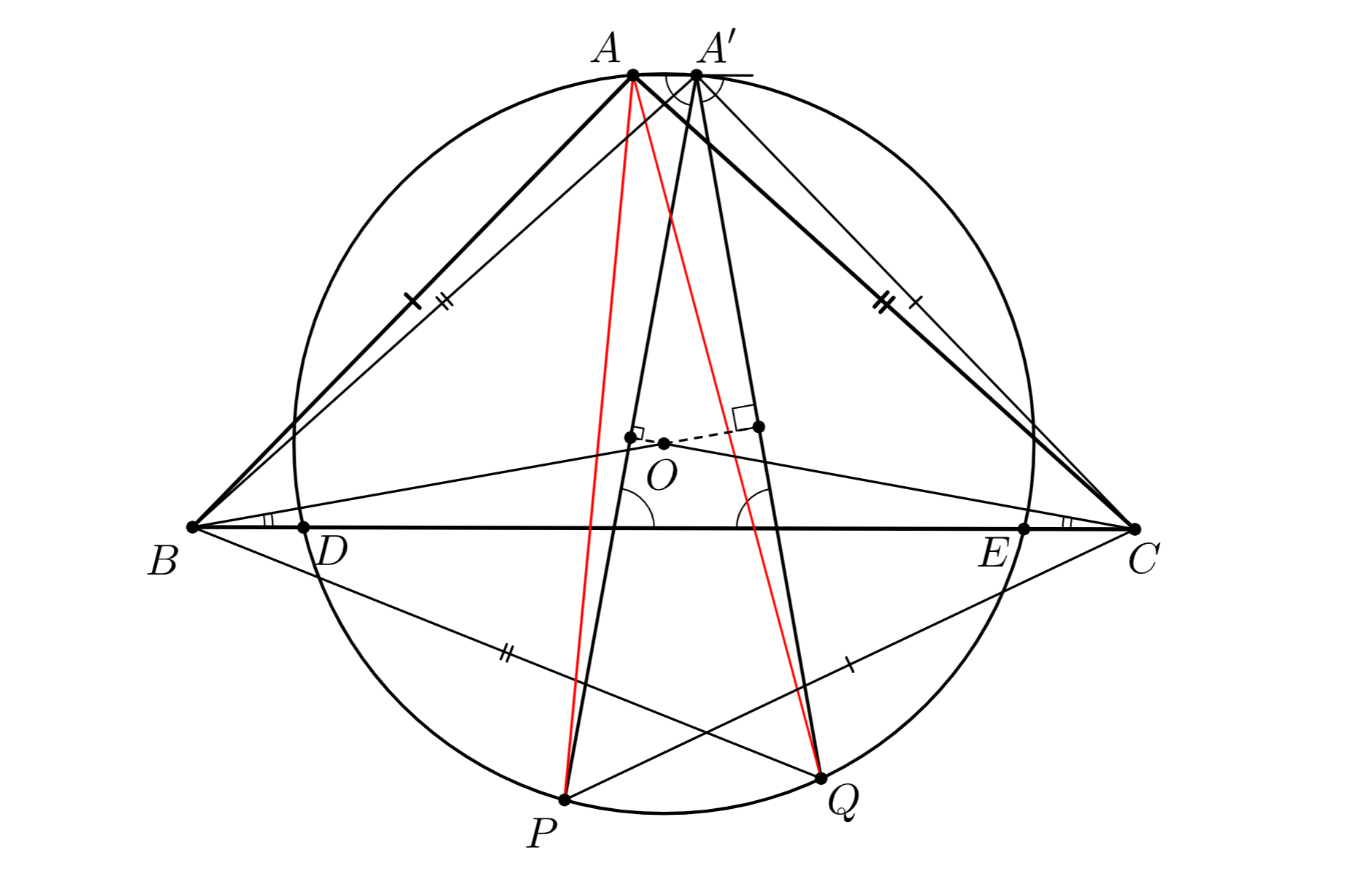
Первое решение. Без ограничения общности будем считать, что точка лежит на отрезке
и
Пусть
— центр
окружности
Пусть точка
симметрична
относительно серединного перпендикуляра к отрезку
(см. первый рисунок). Из
симметрии
Окружность с центром и радиусом
пересекает окружность
в точках, симметричных относительно прямой
то
есть точки
и
симметричны относительно
Аналогично, точки
и
симметричны относительно прямой
Прямые и
симметричны относительно серединного перпендикуляра к отрезку
поэтому они образуют равные углы с
прямой
Поскольку
и
то прямые
и
образуют равные углы с прямой
Значит, меньшие дуги окружности
стягиваемые хордами
и
равны, а тогда
что и
требовалось.
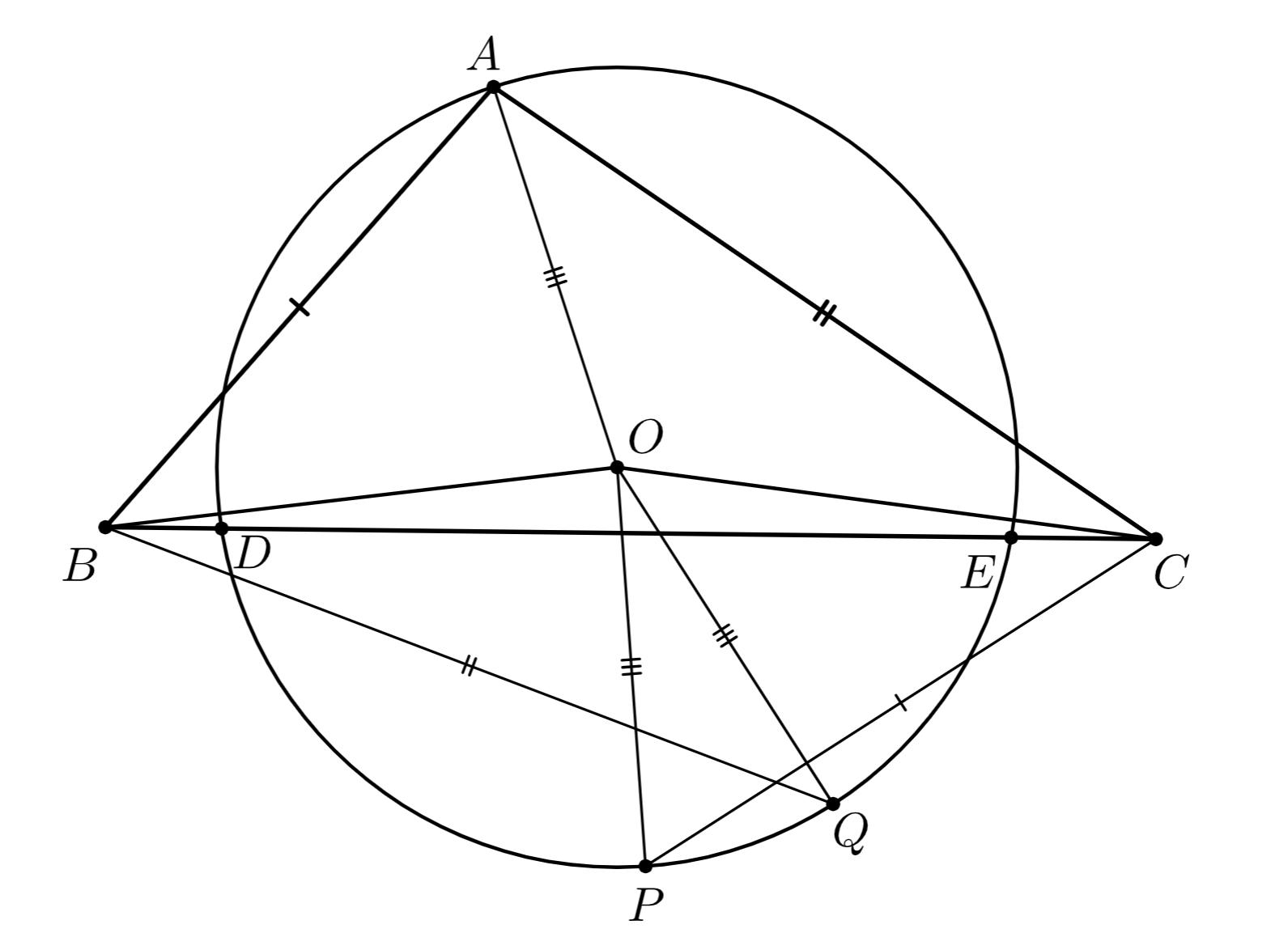
Второе решение. Без ограничения общности будем считать, что точка лежит на отрезке
Пусть
— центр окружности
Заметим, что
Поскольку
то точки и
лежат по одну сторону от прямой
(см. второй рисунок). Треугольники
и
равны по трем сторонам,
треугольники
и
— тоже.
Тогда
(Если луч не лежит внутри угла
то луч
лежит внутри угла
а значит и внутри угла
В этом случае
либо
либо
в обоих случаях получаем противоречие с равенством треугольников и
Аналогично, луч
лежит внутри угла
)
Поэтому треугольники и
равны по двум сторонам и углу между ними, откуда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




