Тема Регион 10 класс

Регион 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31258Максимум баллов за задание: 7

В окружность $Ω$ вписан шестиугольник $AECDBF$ . Известно, что точка $D$ делит дугу $BC$ пополам, а треугольники $ABC$ и $DEF$ имеют общую вписанную окружность. Прямая $BC$ пересекает отрезки $DF$ и $DE$ в точках $X$ и $Y$ , а прямая $EF$ пересекает отрезки $AB$ и $AC$ в точках $Z$ и $T$ соответственно. Докажите, что точки $X,Y,T,Z$ лежат на одной окружности.

Источники: ВСОШ, РЭ, 2022, 10.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Из-за общей вписанной окружности добываем ещё одну биссектрису и, соответственно, середину дуги

Подсказка 2

Раз проведены из середин дуг отрезки, то поможет лемма, что всегда получается добыть ещё вписанность (посчитайте угол между хордами и вписанный угол)

Подсказка 3

Явно же не хочется в XYTZ проводить что-то такое и считать углы, значит, надо будет считать отрезки. А счёт отрезков для вписанных четырёхугольников это степень точки писать

Подсказка 4

Рассмотрите случай, когда стороны XYTZ параллельны, а в ином случае можно пересечь и реализовать план пункта 2

Показать доказательство

Пусть $I$ — центр общей вписанной окружности $ω$ треугольников $ABC$ и $DEF$ . Так как $D$ — середина дуги $BC$ , точки $A,$ $I,$ $D$ лежат на одной прямой. Окружность $ω$ вписана в угол $∠FDE,$ поэтому $DI$ — биссектриса угла $∠F DE,$ а точка $A$ — середина дуги $FE.$ Сформулируем и докажем следующее утверждение.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Дана окружность и её хорда $BC.$ Точка $D$ — середина одной из дуг $BC.$ Через $D$ провели две прямые, которые пересекают прямую $BC$ и окружность в точках $X,$ $F$ и $Y,$ $E.$ Тогда точки $E,$ $F,$ $X,$ $Y$ лежат на одной окружности.

Доказательство 1. Из равенства углов

1 ⌢ ⌢ 1 ⌢ ⌢ ∠F ED = 2(FB+ BD )= 2(F B+ CD )=∠F XB

следует искомая вписанность.

$PIC$

____________________________________________________________________________________________________

Доказательство 2. Заметим, что $∠BF D =∠BCD =∠DBC.$ Тогда описанная окружность треугольника $BXF$ касается прямой $BD,$ поэтому $DB2 = DX ⋅DF.$ Аналогично $DB2 = DY ⋅DE.$ Следовательно, точке $E,$ $F,$ $X,$ $Y$ лежат на одной окружности.

$PIC$

____________________________________________________________________________________________________

Лемма доказала вписанность $EFXY.$ Аналогично, четырёхугольник $BCT Z$ — вписанный. Если $BC ||EF,$ то конструкция симметрична относительно прямой $AD,$ и утверждение задачи очевидно. Рассмотрим точку $S$ пересечения $F E$ и $BC.$ Приравнивая произведения отрезков секущих для окружностей $Ω,$ $(BCT Z)$ и $(FEY X)$ (т.е. степень точки $S$ относительно окружностей), получаем равенства

SX⋅SY = SF ⋅SE = SB⋅SC = SZ⋅ST

Из $SX ⋅SY =SZ ⋅ST$ следует, что точки $X,$ $Y,$ $Z,$ $T$ лежат на одной окружности.

$PIC$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#79752Максимум баллов за задание: 7

Пусть $P(x)= a xn+ a xn−1+ ...+ ax +a , n n−1 1 0$ где $n$ — натуральное число. Известно, что числа $a,a ,...,a 0 1 n$ — целые, при этом $an ⁄=0,an−k = ak$ при всех $k= 0,1,...,n,$ и $an+ an−1+ ...+a1 +a0 = 0.$ Докажите, что число $P(2022)$ делится на квадрат некоторого натурального числа, большего $1.$

Источники: Всеросс., 2022, РЭ, 10.4(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Понятно, что константа здесь взята с неба (так как коэффициенты могут быть любыми числами). Поэтому опираться на 2022 не нужно. Будем доказывать задачу в общем виде, то есть, что P(x) делится на квадрат некоторого целого числа при любом целом x (c ограничением > 1 разберёмся позже).

Подсказка 2:

То есть хотим доказать, что P(x) = Н(х)Q(x)², где Q(x), H(x) ∈ ℤ[x]. Подумаем, какая степень может быть у Q(x)?

Подсказка 3:

В теории, конечно, любая, только вот как доказывать? Доказывать делимость на квадратный трёхчлен уже не самая простая задача, а что говорить про большие степени? Поэтому стоит начать с многочлена Q(x), равного линейной функции, а если не сработает, то придётся страдать...

Подсказка 4:

Хотим доказать, что P(x) делиться на многочлен (x − с)², где с ∈ ℤ. Сейчас Вам предстоит запомнить идею. То, что мы хотим доказать, равносильно тому, что P(x + c) делится на x² (осознайте самостоятельно, чтоб получить удовольствие от задачи). А делимость на x² гораздо более простой в доказательстве факт, чем делимость на другую квадратичную функцию. Как же его доказать?

Подсказка 5:

Введём обозначения для красоты и удобства. Пусть t = x − c, а также R(t) = P(t + c). Хотим доказать, что P(t + с) делится на t², то есть, что R(t) делится на t². Что это значит?

Подсказка 6:

Что у R(t) должны быть нулевыми свободный коэффициент и коэффициент при t. Начнём со свободного. Как изящно получить свободный коэффициент с помощью R(t)?

Подсказка 7:

Подставить 0! R(0) — и есть свободный коэффициент. То есть хотим доказать, что aₙcⁿ + aₙ₋₁cⁿ⁻¹ + ... + a₁c + a₀ = 0, однако по условию мы знаем, что aₙ + aₙ₋₁ + ... + a₁ + a₀ = 0. На какие мысли о "с" это наталкивает?

Подсказка 8:

Разумеется, что нужно взять с = 1, тогда мы сразу докажем, что свободный коэффициент нулевой. Остаётся разобраться с коэффициентом перед t. Его уже простой подстановкой не узнать, придётся считать честно...

Подсказка 9:

Но и это не беда! R(t) = aₙ(t + 1)ⁿ + aₙ₋₁(t + 1)ⁿ⁻¹ + ... + a₁(t+1) + a₀ = 0. Вспомним про бином Ньютона и поймём, что коэффициент при t это naₙ + (n − 1)aₙ₋₁ + ... + a₁. Хотим доказать, что это выражение равно 0. Пока что непонятно, как это делать, но ведь мы ещё никак не воспользовались условием про симметричность коэффициентов...

Подсказка 10:

naₙ + (n − 1)aₙ₋₁ + ... + a₁ = 0 равносильно тому, что aₙ₋₁ + 2aₙ₋₂ ... + (n − 1)a₁ + na₀ (в силу симметрии). Очень уж красиво дополняют друг друга эти выражения, которые численно равны. Причём мы хотим, чтоб они численно были равны 0. Может быть, их тогда стоит сложить?... А изначальное ограничение на 1 разрешится само собой) Дальше мы замолкаем. Успехов!

Показать доказательство

Достаточно доказать утверждение: многочлен $P (x)$ делится на $(x − 1)2.$ Действительно, после деления (например, столбиком), в частном получится многочлен $Q(x)$ с целыми коэффициентами, и тогда равенство многочленов $2 P(x)= (x− 1)Q (x)$ влечет равенство $2 P (2022)= 2021 ⋅Q (2022),$ из которого следует утверждение задачи, поскольку $Q(2022)$ — целое число.

Для доказательства утверждения сделаем замену $t= x− 1,$ положим $n n−1 R(t)= P(t+1)= an(t+ 1) +an−1(t+1) + ...+a1(t+1)+ a0$ и докажем, что $R(t)$ делится на $2 t ,$ т.е. что последние два коэффициента многочлена $R(t)$ равны $0.$

Свободный член многочлена $R$ равен $R(0) =an+ an−1+ ...+ a0 =0.$ Поскольку в многочлене $k (t+ 1)$ коэффициент при $t$ равен $k,$ коэффициент при $t$ многочлена $R$ равен $nan+ (n − 1)an−1 +...+ a1.$ Из условий $an−k = ak$ следует, что удвоенный коэффициент при $t$ равен $(nan+ (n − 1)an−1 +...+a1)+(na0+ (n − 1)a1+...+an−1)= n(an+ an−1+ ...+a0)= 0.$ Тем самым, задача решена.

Ошибка.
Попробуйте повторить позже

Задача 3#88689Максимум баллов за задание: 7

Дан квадратный трехчлен $P (x)$ . Докажите, что существуют попарно различные числа $a$ , $b$ и $c$ такие, что выполняются равенства

P(b+c)= P(a),P(c+ a)= P(b),P (a +b)= P(c).

Источники: ВСОШ, РЭ, 2022, 10.2 и 11.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Очень полезно уметь представлять такие задачи. Мы знаем, что Р(х) --- это трёхчлен. Как выглядит его график?

Подсказка 2

Это парабола! Вспомним, что парабола симметрична относительно некоторой вертикальной прямой. А если значения в двух различных точках параболы равны, то что можно сказать про эти точки?

Подсказка 3

Они равноудалены от абсциссы вершины параболы! Теперь подумайте, чему равна сумма таких точек, и из этого приведите пример к задаче.

Показать доказательство

Пусть $d$ — абсцисса вершины параболы $y =P(x)$ , так что прямая $x= d$ — ось симметрии параболы. Тогда для любых чисел $t$ и $s$ с суммой $2d$ (т.е. таких, что точки $t$ и $s$ симметричны относительно $d)$ выполнено $P(t)= P(s)$ .

Таким образом, любая тройка попарно различных чисел $a,b,c$ с суммой $2d$ будет удовлетворять условию задачи. Можно взять, скажем,

2d 2d 2d a =-3 − 1,b= 3-,c= 3-+1.

Ошибка.
Попробуйте повторить позже

Задача 4#134306Максимум баллов за задание: 7

Петя написал на доске десять натуральных чисел, среди которых нет двух равных. Известно, что из этих десяти чисел можно выбрать три числа, делящихся на 5. Также известно, что из написанных десяти чисел можно выбрать четыре числа, делящихся на 4. Может ли сумма всех написанных на доске чисел быть меньше 75?

Источники: ВСОШ, РЭ, 2022, 9.1, 10.1 и 11.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать пример таких чисел.

Подсказка 2:

Добавьте в набор число 20. Оно одновременно делится на 4 и на 5. Осталось взять два маленьких числа, кратных 5, и три числа, кратных 4.

Показать ответ и решение

Пример: $1,$ $2,$ $3,$ $4,$ $5,$ $6,$ $8,$ $10,$ $12,$ $20.$ В этом наборе три числа $(5,10,20)$ делятся на 5, четыре числа $(4,8,12,20)$ делятся на 4, а общая сумма равна $71.$

Ответ:

может

Ошибка.
Попробуйте повторить позже

Задача 5#134326Максимум баллов за задание: 7

У Васи есть $n$ конфет нескольких сортов, где $n ≥145.$ Известно, что если из данных $n$ конфет выбрать любую группу, содержащую не менее 145 конфет (в частности, можно выбрать группу из всех данных $n$ конфет), то существует такой сорт конфет, что выбранная группа содержит в точности 10 конфет этого сорта. Найдите наибольшее возможное значение $n.$

Источники: ВСОШ, РЭ, 2022. 10.3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Пусть имеется n конфет. Рассмотрим все сорта конфет, для каждого из которых в наборе есть ровно 10 конфет этого сорта. Пусть их k. Очевидно, что какой-то из них является тем самым сортом из условия задачи.

Подсказка 2:

Подумайте, как можно нарушить выполнимость условия.

Подсказка 3:

Уберем по 1 конфете каждого из k сортов. Для оставшегося набора из n – k конфет условие не выполняется. Попробуйте оценить величину n – k.

Подсказка 4:

Очевидно, что n ≥ 10k, откуда n/10 ≥ k. Следовательно, n – k ≥ 9n/10. Как мы поняли ранее, этот набор не удовлетворяет условию. Значит, в нём менее 145 конфет. Теперь можно сделать оценку. Не забудьте придумать пример.

Показать ответ и решение

Оценка. Докажем, что $n> 160$ «не работает».

Пусть дан набор из $n$ конфет. Назовём сорт критическим, если конфет этого сорта ровно 10 (среди всех данных $n$ конфет). Пусть у нас $k$ критических сортов, тогда всего конфет не менее $10k:$ $n ≥10k.$ Уберём по одной конфете каждого критического сорта и организуем группу из оставшихся $n − k$ конфет. Для этой группы нет сорта, представленного ровно 10 конфетами. Кроме того,

n 9n 9⋅160 n− k≥ n− 10 = 10 >-10--=144.

Значит, в рассматриваемой группе не менее 145 конфет, поэтому условие задачи не выполняется.

Пример. Теперь приведём пример ситуации, в которой у Васи может быть 160 конфет. Пусть у него есть ровно по 10 конфет 16 сортов. Пусть выбрана группа, для которой нет сорта, представленного ровно 10 конфетами. Тогда в эту группу не входит хотя бы одна конфета каждого сорта (иначе говоря, ни один сорт не будет взят полностью), т.е. группа содержит не более $16 ⋅9 =144$ конфет, значит, условие задачи выполнено.

Ответ:

160

Ошибка.
Попробуйте повторить позже

Задача 6#135017Максимум баллов за задание: 7

На плоскости отмечены $N$ точек. Любые три из них образуют треугольник, величины углов которого в градусах выражаются натуральными числами. При каком наибольшем $N$ это возможно?

Источники: ВСОШ, РЭ, 2022, 9.9 и 10.8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте сначала какой-нибудь пример. Ясно, что точки надо отмечать не каким-то произвольным образом на плоскости. Например, можно отмечать их на окружности, ведь там легко вычисляются углы.

Подсказка 2:

Итак, вы придумали пример на 180 и теперь хотите сделать оценку. Если нет, то придумайте. Попробуйте найти угол, образованный тремя отмеченными точками, внутри которого лежат остальные точки.

Подсказка 3:

Для этого можно ввести координаты, выбрать точку A с наибольшей ординатой и две точки B, C такие, что угол BAC максимален. Теперь подумайте, какое возникнет противоречие, если внутри угла будет хотя бы 178 отмеченных точек.

Показать ответ и решение

Пример. Покажем сначала, что при $N = 180$ требуемое возможно. Отметим на окружности 180 точек, разбивающих её на 180 равных дуг величиной по $∘ 2$ каждая. Величина любой дуги с концами в двух из отмеченных точек выражается чётным числом градусов, поэтому величина любого вписанного в окружность угла, образованного тремя отмеченными точками, выражается натуральным числом градусов. Следовательно, 180 отмеченных точек удовлетворяют условию задачи.

Теперь докажем оценку $N ≤ 180,$ это можно сделать несколькими способами.

_________________________________________________________________________________________________________________________________________________________________________________

Первый способ. Осталось доказать, что $N ≤ 180.$ Любые три отмеченных точки образуют треугольник, поэтому не могут лежать на одной прямой. Считая отмеченные точки расположенными на координатной плоскости, обозначим через $A$ любую из них с максимальной ординатой. Среди оставшихся выберем точки $B$ и $C$ такие, что угол $BAC$ максимален.

Из условия задачи следует, что в треугольнике $ABC$ величины углов $ABC$ и $ACB$ не меньше $1∘,$ поэтому величина угла $BAC$ не больше $178∘.$ Ввиду выбора точек $B$ и $C$ остальные $N − 3$ отмеченные точки лежат строго внутри угла $BAC,$ и каждый луч с началом в точке $A$ содержит не больше одной из них. Проведя через каждую отмеченную точку внутри угла $BAC$ луч с началом в точке $A,$ получим $N − 3$ различных луча, делящих $∠BAC$ на $N − 2$ угла. Если $N − 2> 178,$ то хотя бы один из этих углов имеет величину, меньшую $1∘,$ и является углом некоторого треугольника с вершинами в трёх отмеченных точках, что противоречит условию задачи. Следовательно, $N − 2≤ 178,$ то есть $N ≤180,$ что и требовалось доказать.

_________________________________________________________________________________________________________________________________________________________________________________

Второй способ. Рассмотрим пару отмеченных точек $A,$ $B$ на наибольшем расстоянии друг от друга. Тогда для любой другой отмеченной точки $C$ сторона $AB$ — наибольшая в треугольнике $ABC,$ поэтому, в частности, угол $∠BAC$ острый.

Проведя из точки $A$ лучи во все отмеченные точки, получаем, что все эти лучи различны (ибо три отмеченных точки не могут лежать на одной прямой), и каждый составляет с лучом $AB$ острый угол, выражаемый целым числом градусов. Такой угол (если луч не совпадает с $AB$ ) может принимать значения от $1∘$ до $89∘,$ поэтому количество таких лучей $N − 2$ не превосходит $2⋅89= 178.$ Отсюда $N ≤ 180.$

Ответ:

180

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#135020Максимум баллов за задание: 7

Докажите, что существует натуральное число $b$ такое, что при любом натуральном $n> b$ сумма цифр числа $n!$ не меньше $100 10 .$

Источники: ВСОШ, РЭ, 2022, 9.10 и 10.10 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Нужна какая-нибудь лемма, которая позволит оценивать сумму цифр некоторых чисел. Условие задачи даёт много свободы, можно выбрать любое b. Значит, возможно, получится подогнать задачу под лемму.

Подсказка 2:

Через s(m) обозначим сумму цифр числа m. Если натуральное число m кратно 10ᵏ − 1, где k — также натуральное, то s(m) ≥ 9k. Докажите этот факт.

Подсказка 3:

Попробуйте доказывать по индукции. Распишите число m в виде 10ᵏu + v и сведите к меньшему числу.

Подсказка 4:

Для доказательства перехода понадобится следующий факт: s(a) + s(b) ≥ s(a + b). Докажите его, используя сложение в столбик.

Показать доказательство

Положим $a= 10100.$ Через $s(m)$ обозначим сумму цифр числа $m.$ Отметим простое свойство $s(ℓ)+ s(m) ≥s(ℓ+m ),$ которое сразу видно, если числа $ℓ$ и $m$ сложить в столбик.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Пусть $k$ — натуральное число, и пусть натуральное число $m$ кратно $k 10 − 1.$ Тогда $s(m)≥ 9k.$

Доказательство. Индукция по $m.$ База $k m =10 − 1$ очевидна.

Предположим, что $k m ≥ 10 ,$ и что утверждение доказано для всех чисел, меньших $m.$ Докажем его и для $m.$ Пусть последние $k$ цифр числа $m$ образуют число $v$ (возможно, с ведущими нулями), а все остальные — число $u >0$ (иначе говоря, $-- k m =uv =10 u+ v$ ). Поскольку $m$ делится на $k 10 − 1,$ то и (положительное) число

m′ = u+ v = m − (10k− 1)u

также кратно $k 10 − 1.$ Поэтому $′ s(m )≥ 9k$ по предположению индукции, а тогда

′ s(m )=s(u)+s(v) ≥s(u+v)= s(m )≥ 9k.

______________________________________________________________________________________________________________________________________________________

Для решения задачи осталось взять такое $k,$ что $9k ≥a,$ и заметить, что если $b= 10k− 1$ и $n ≥b,$ то $n!$ делится на $10k − 1$ и, значит, $s(n!)≥ 9k ≥a.$

Ошибка.
Попробуйте повторить позже

Задача 8#135021Максимум баллов за задание: 7

На доске написаны три последовательных нечётных числа. Может ли сумма остатков от деления этих трёх чисел на 2022 равняться некоторому простому числу?

Источники: ВСОШ, РЭ, 2022, 10.6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте в явном виде записать суммы этих остатков. Обозначьте остаток первого числа через r и посмотрите, что получится.

Подсказка 2:

Вероятно, вы столкнулись с проблемой, что в некоторых случаях остатки двух других чисел будут выглядеть r + 2 и r + 4, а в некоторых других — иначе. Разберите эти случаи отдельно.

Показать ответ и решение

Пусть $r$ — остаток меньшего из данных нечётных чисел при делении на 2022, так что $r$ — некоторое нечётное число множества ${1,3,5,$ …, $2021}.$ Если $r≤2017,$ то два других остатка — $r+2$ и $r+ 4,$ так что сумма остатков равна

r+ (r+2)+ (r+ 4)= 3(r+ 2).

Это число составное, так как делится на 3 и больше 3. Отдельно рассмотрим случаи $r =2019$ и $r=2021.$ В первом случае остатки данных чисел равны 2019, 2021 и 1. Во втором случае остатки данных чисел равны 2021, 1 и 3. В обоих случаях сумма остатков делится на 3 и больше 3.

Ответ:

не может

Ошибка.
Попробуйте повторить позже

Задача 9#135022Максимум баллов за задание: 7

Дан вписанный четырёхугольник $ABCD,$ в котором $∠A = 2∠B.$ Биссектриса угла $C$ пересекает сторону $AB$ в точке $E.$ Докажите, что $AD + AE = BE.$

Показать доказательство

Решение

Обозначим $∠ABC =α,$ тогда по условию $∠DAB = 2α.$ На продолжении отрезка $AB$ за точку $A$ отметим точку $F$ так, что $AD = AF.$ Тогда треугольник $AF D$ равнобедренный, и его углы при основании равны. Так как $∠FAD = 180∘− 2α,$ то

∠AFD = ∠ADF = α.

Поскольку четырехугольник $ABCD$ — вписанный, то

∠ADC =180∘− ∠ABC = 180∘− α= 180∘− ∠ADF.

Следовательно, точки $C,$ $D$ и $F$ лежат на одной прямой. Тогда

∠CFB = α= ∠CBF,

поэтому треугольник $FCB$ равнобедренный. Значит, его биссектриса $CE$ совпадает с медианой. Итого,

BE = EF =AD + AE,

что и требовалось.

$PIC$

_________________________________________________________________________________________________________________________________________________________________________________

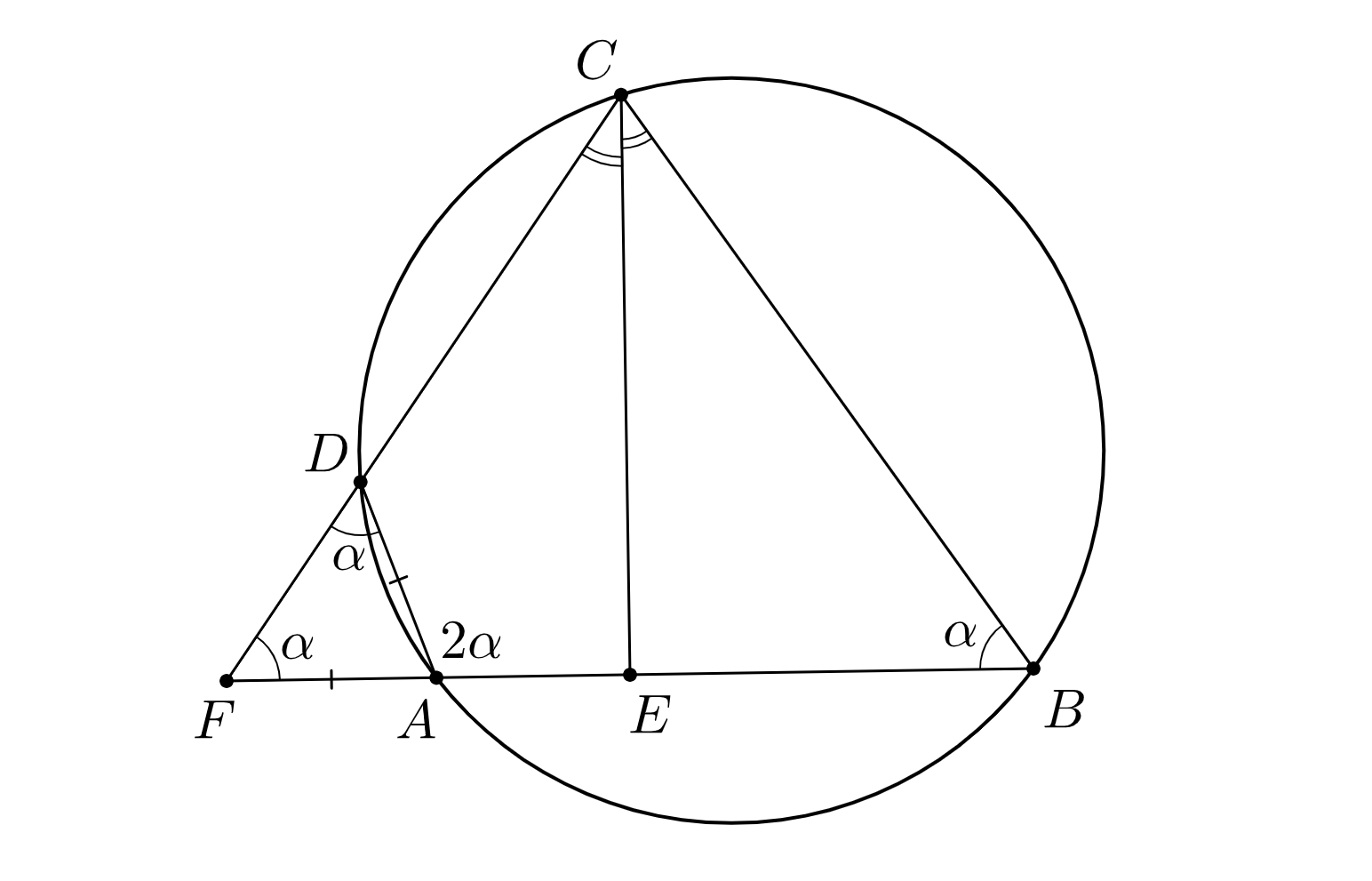
Замечание. Существует и такая вариация решения. Обозначим $∠ABC = α,$ тогда по условию $∠DAB =2α.$ Из вписанности четырёхугольника $ABCD$ имеем

∠BCD = 180∘− ∠DAB =180∘− 2α.

Тогда

∠BCD + ∠ABC = 180∘− α,

лучи $BA$ и $CD$ пересекаются в некоторой точке $F,$ и при этом $∠BF C = α.$ Поскольку

∠CFB = α= ∠CBF,

треугольник $F CB$ равнобедренный. Значит, его биссектриса $CE$ совпадает с медианой, поэтому

BE = EF =AF + AE.

Для завершения решения остаётся показать, что $AF =AD.$ Это следует из вписанности четырёхугольника $ABCD,$ поскольку

∠ADF = ∠CBF = α.

Значит, треугольник $AF D$ равнобедренный с равными углами

∠AFD = ∠ADF = α.

Ошибка.
Попробуйте повторить позже

Задача 10#135023Максимум баллов за задание: 7

В вершины правильного 100-угольника поставили 100 фишек, на которых написаны номера 1, 2, …, 100, именно в таком порядке по часовой стрелке. За ход разрешается обменять местами некоторые две фишки, стоящие в соседних вершинах, если номера этих фишек отличаются не более чем на $k.$ При каком наименьшем $k$ серией таких ходов можно добиться расположения, в котором каждая фишка сдвинута на одну позицию по часовой стрелке (по отношению к своему начальному положению)?

Источники: ВСОШ, РЭ, 2022, 10.9 и 11.8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать пример, он почти очевидный.

Подсказка 2:

Ясно, что такое можно реализовать для k = 50. Достаточно просто 99 раз сдвинуть фишку 50 против часовой стрелки.

Подсказка 3:

Чтобы доказать оценку на 50, попробуйте рассмотреть промежуток на окружности между фишками 1 и 100, который изначально без фишек.

Подсказка 4:

Попробуйте сравнить количество входов и заходов каждой из остальных фишек эту дугу. Также подумайте, через какую фишку 1 или 100 на дугу могут заходить другие фишки.

Показать ответ и решение

Пример. Фишку 50 последовательно 99 раз меняем со следующей против часовой стрелки. Получаем требуемое расположение.

Есть несколько способов доказать оценку, ниже мы приведём два из них.

Первый способ. Предположим, что при некотором $k <50$ требуемая расстановка получена.

В каждый момент времени считаем покрашенной дугу от фишки 100 до фишки 1 по часовой стрелке. Так как фишки 100 и 1 нельзя поменять за один ход, каждая конкретная фишка $m$ $(2≤ m ≤99)$ могла попасть на покрашенную дугу или покинуть покрашенную дугу лишь путём обмена с одной из фишек 1 или 100.

Поскольку изначально и в конце фишка $m$ не была на покрашенной дуге, она сделала одинаковое количество входов на покрашенную дугу и выходов с покрашенной дуги. При $m ≤50$ фишка $m$ не могла меняться с фишкой 100, поэтому она могла делать вход или выход только путём обмена с фишкой 1. При входе фишка 1 совершает сдвиг на 1 по часовой стрелке, а при выходе — на 1 против часовой стрелки. Проведём аналогичные рассуждения для фишек $m ≥ 51,$ которые не могут меняться с фишкой 1.

Тем самым, мы получаем, что фишки 1 и 100 совершают одинаковый сдвиг по и против часовой стрелки, поэтому они остаются на своих позициях. Противоречие.

_________________________________________________________________________________________________________________________________________________________________________________

Второй способ. Будем считать сдвиги фишек относительно их начальной позиции, причём сдвиг по часовой стрелке будет считаться с плюсом, против часовой — с минусом. Тогда при обмене двух фишек к сдвигу одной из них прибавляется +1, а другой — $− 1.$ Значит, в результате проведённых операций общая сумма сдвигов будет равна 0.

Рассуждаем от противного: пусть при $k <50$ каждая фишка $i$ в итоге сдвинута на одну позицию по часовой стрелке, т.е. её сдвиг оказался равным $1+100ti$ (здесь $ti$ — целое «число оборотов» по часовой стрелке, в частности при $ti <0$ фишка $i$ сделала $|ti|$ оборотов против часовой стрелки). Тогда суммарный сдвиг всех 100 фишек равен

100(t1+ t2+...+t100)+ 100.

Поскольку он должен равняться 0, имеем

t1+ t2 +...+ t100 = −1.

Поскольку $k< 50,$ фишки с номерами $i$ и $j,$ где $j ≥i+ 50,$ не могли меняться местами, поэтому их сдвиги в любой момент заведомо отличаются меньше чем на 100, значит количества оборотов $ti$ и $tj$ равны при $j ≥i+ 50.$ Отсюда имеем $t1 =t51,$ $t2 = t52,$ …, $t50 =t100,$ Тогда сумма

t1+ t2+ ...+ t100 = 2(t1+ t2+ ...+ t50)

— чётна, а значит не равна $− 1.$ Противоречие.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 11#137296Максимум баллов за задание: 7

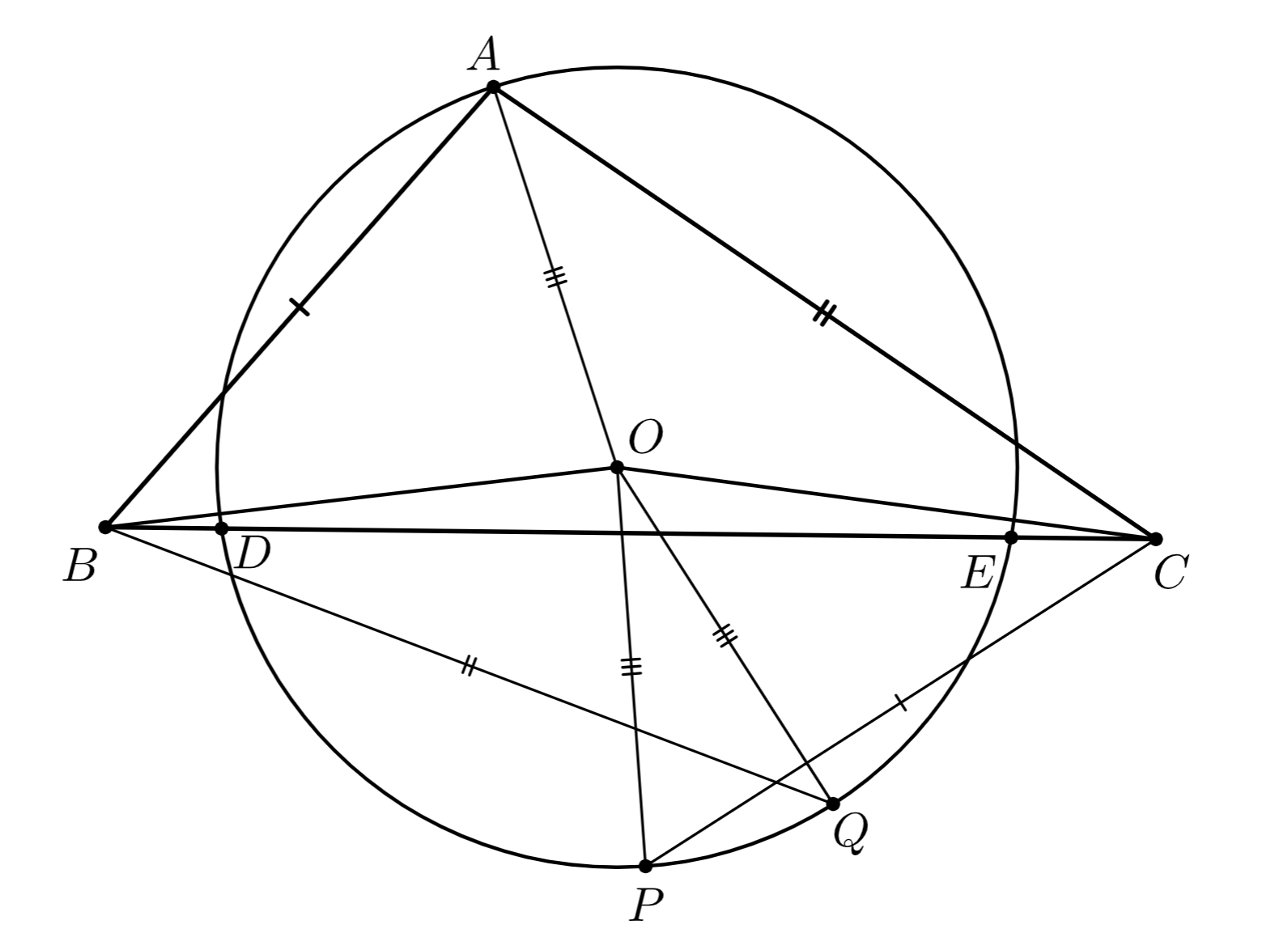
На стороне $BC$ остроугольного треугольника $ABC$ отмечены точки $D$ и $E$ так, что $BD = CE.$ На дуге $DE$ описанной окружности треугольника $ADE,$ не содержащей точку $A,$ нашлись такие точки $P$ и $Q,$ что $AB = PC$ и $AC = BQ.$ Докажите, что $AP = AQ.$

Источники: ВСОШ, ЗЭ, 2022, 10.2 (см. olympiads.mccme.ru)

Показать доказательство

Первое решение. Без ограничения общности будем считать, что точка $D$ лежит на отрезке $BE$ и $AD ≤ AE.$ Пусть $O$ — центр окружности $(ADE ).$ Пусть точка $′ A$ симметрична $A$ относительно серединного перпендикуляра к отрезку $DE$ (см. первый рисунок). Из симметрии

′ A B =AC = BQ.

Окружность с центром $B$ и радиусом $BA ′$ пересекает окружность $(ADE )$ в точках, симметричных относительно прямой $BO,$ то есть точки $A′$ и $Q$ симметричны относительно $BO.$ Аналогично, точки $A′$ и $P$ симметричны относительно прямой $CO.$

Прямые $OB$ и $OC$ симметричны относительно серединного перпендикуляра к отрезку $DE,$ поэтому они образуют равные углы с прямой $DE.$ Поскольку $′ AP ⊥ CO,$ $′ A Q ⊥BO$ и $′ AA ∥DE,$ то прямые $′ A Q$ и $′ A P$ образуют равные углы с прямой $′ AA .$ Значит, меньшие дуги окружности $(ADE),$ стягиваемые хордами $AP$ и $AQ$ равны, а тогда $AP = AQ,$ что и требовалось.

$PIC$

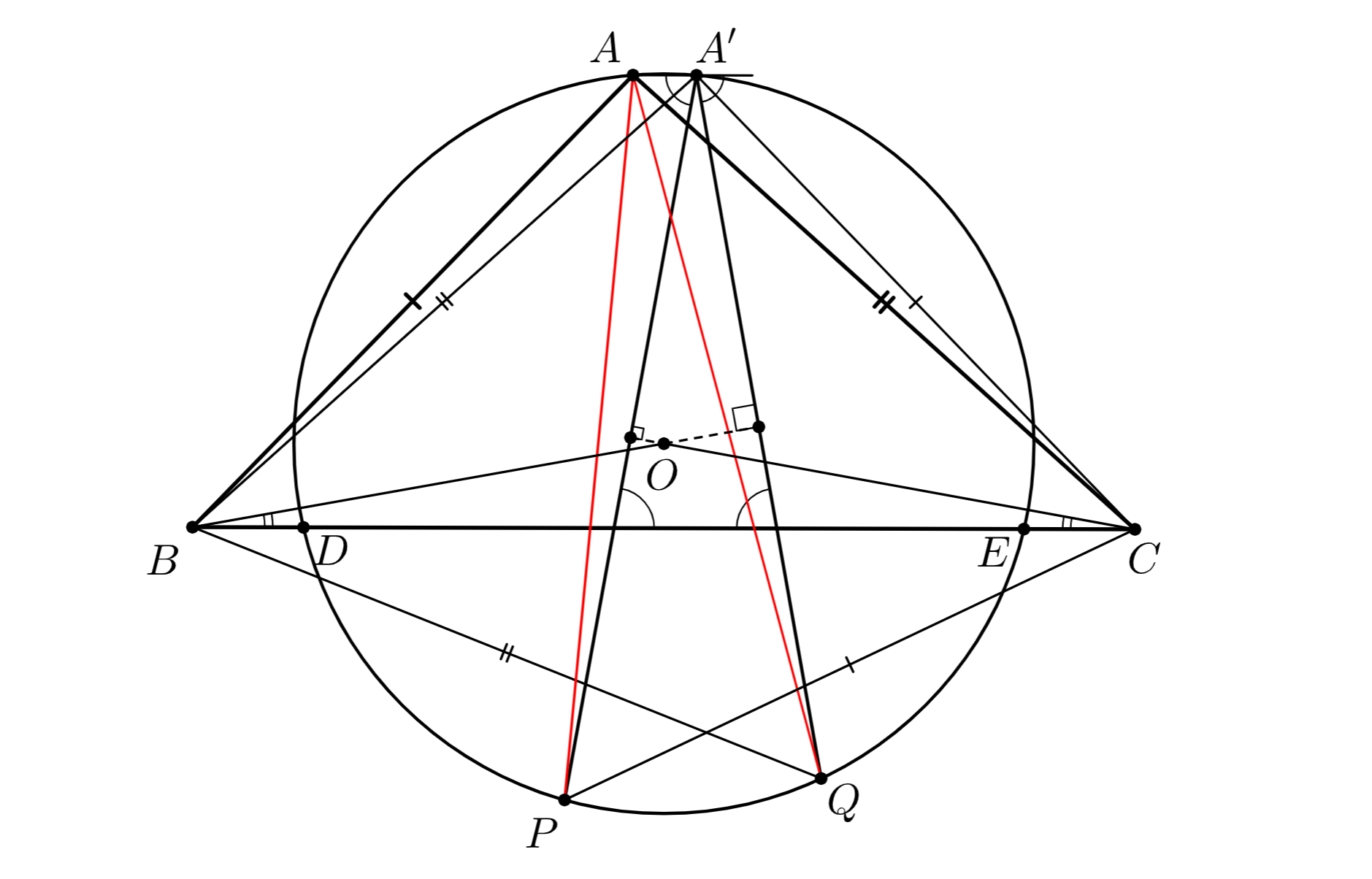
Второе решение. Без ограничения общности будем считать, что точка $D$ лежит на отрезке $BE.$ Пусть $O$ — центр окружности $(ADE ).$ Заметим, что $OB = OC.$ Поскольку

∠DAE < ∠BAC < 90∘,

то точки $A$ и $O$ лежат по одну сторону от прямой $BC$ (см. второй рисунок). Треугольники $OAB$ и $OPC$ равны по трем сторонам, треугольники $OAC$ и $OQB$ — тоже.