Тема Регион 10 класс

Регион 2017

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#73209Максимум баллов за задание: 7

Изначально на доске записаны несколько натуральных чисел (больше одного). Затем каждую минуту на доску дописывается число, равное сумме квадратов всех уже записанных на ней чисел (так, если бы на доске изначально были записаны числа $1,2,2,$ то на первой минуте было бы дописано число $2 2 2 1 + 2 +2$ ). Докажите, что сотое дописанное число имеет хотя бы $100$ различных простых делителей.

Источники: Всеросс., 2017, РЭ, 10.6(см. olympiads.mccme.ru)

Показать доказательство

Заменим в условии сто на $n$ и докажем утверждение индукцией по $n.$ Обозначим число, записанное на $n$ -й минуте через $S . n$ Так как $S1 > 1,$ оно имеет хотя бы один простой делитель, то есть база доказана.

Переход. Заметим, что $2 2 2 2 Sn+1 = Sn+ Sn−1+ ...+S1 =Sn +Sn = Sn(Sn+ 1).$ То есть $Sn+1$ делится на все простые делители $Sn$ (по предположению их хотя бы $n$ ), а также оно делится на простой делитель $Sn+ 1,$ отличный от простых делителей $Sn,$ поскольку $(Sn+ 1,Sn)= 1.$ Получили требуемое.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#81579Максимум баллов за задание: 7

Паша выбрал $2017$ (не обязательно различных) натуральных чисел $a ,a ,...,a 1 2 2017$ и играет сам с собой в следующую игру. Изначально у него есть неограниченный запас камней и $2017$ больших пустых коробок. За один ход Паша добавляет в любую коробку (по своему выбору) $a1$ камней, в любую из оставшихся коробок (по своему выбору) — $a2$ камней, $...,$ наконец, в оставшуюся коробку — $a2017$ камней. Пашина цель — добиться того, чтобы после некоторого хода во всех коробках стало поровну камней. Мог ли он выбрать числа так, чтобы цели можно было добиться за $43$ хода, но нельзя — за меньшее ненулевое число ходов?

Источники: Всеросс., 2017, РЭ, 10.3(см. olympiads.mccme.ru)

Показать ответ и решение

Заметим, что $2017= 43⋅46+39.$ Приведём пример Пашиных чисел, при которых требуемое выполняется. Пусть среди его чисел $39$ двоек, $46$ чисел, равных $44,$ а остальные — единицы.

Чтобы добиться требуемого за $43$ хода, Паша выбирает $39$ коробок, в которые он всегда кладёт по два камня — через $43$ хода в них окажется $2⋅43 =86$ камней. Остальные коробки он разбивает на $43$ группы по $46$ коробок; на $i$ -м ходу он положит по $44$ камня во все коробки $i$ -й группы и по одному камню — в коробки остальных групп. Тогда через $43$ хода в каждой коробке каждой группы будет по $44+42⋅1= 86$ камней, то есть во всех коробках будет поровну камней.

Осталось доказать, что за меньшее число ходов требуемое невыполнимо. Пусть Паша сделал $k< 43$ ходов. Тогда в какую-то коробку $A$ попало $44$ камня на одном ходу и в ней будет не меньше, чем $44+ (k− 1)= 43+ k$ камней. С другой стороны, поскольку $46k <2017,$ в какую-то коробку $B$ ни на одном из ходов не попадёт $44$ камня, то есть в ней будет не больше $2k$ камней. Поскольку $k <43,$ имеем $2k< k+ 43,$ а значит, в коробке $B$ меньше камней, чем в $A.$ Таким образом, Паша ещё не добился требуемого.

Ответ:

Да, мог

Ошибка.
Попробуйте повторить позже

Задача 3#96961Максимум баллов за задание: 7

Окружность с центром в точке $I$ вписана в четырёхугольник $ABCD.$ Лучи $BA$ и $CD$ пересекаются в точке $P,$ а лучи $AD$ и $BC$ пересекаются в точке $Q.$ Известно, что точка $P$ лежит на окружности $ω,$ описанной около треугольника $AIC.$ Докажите, что точка $Q$ тоже лежит на окружности $ω.$

Источники: Всеросс., 2017, РЭ, 10.2(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка

В этой задаче нужно просто аккуратно собрать всю информацию про чертëж и через счёт углов показать, что четырëхугольник QAIC вписанный.

Показать доказательство

$PIC$

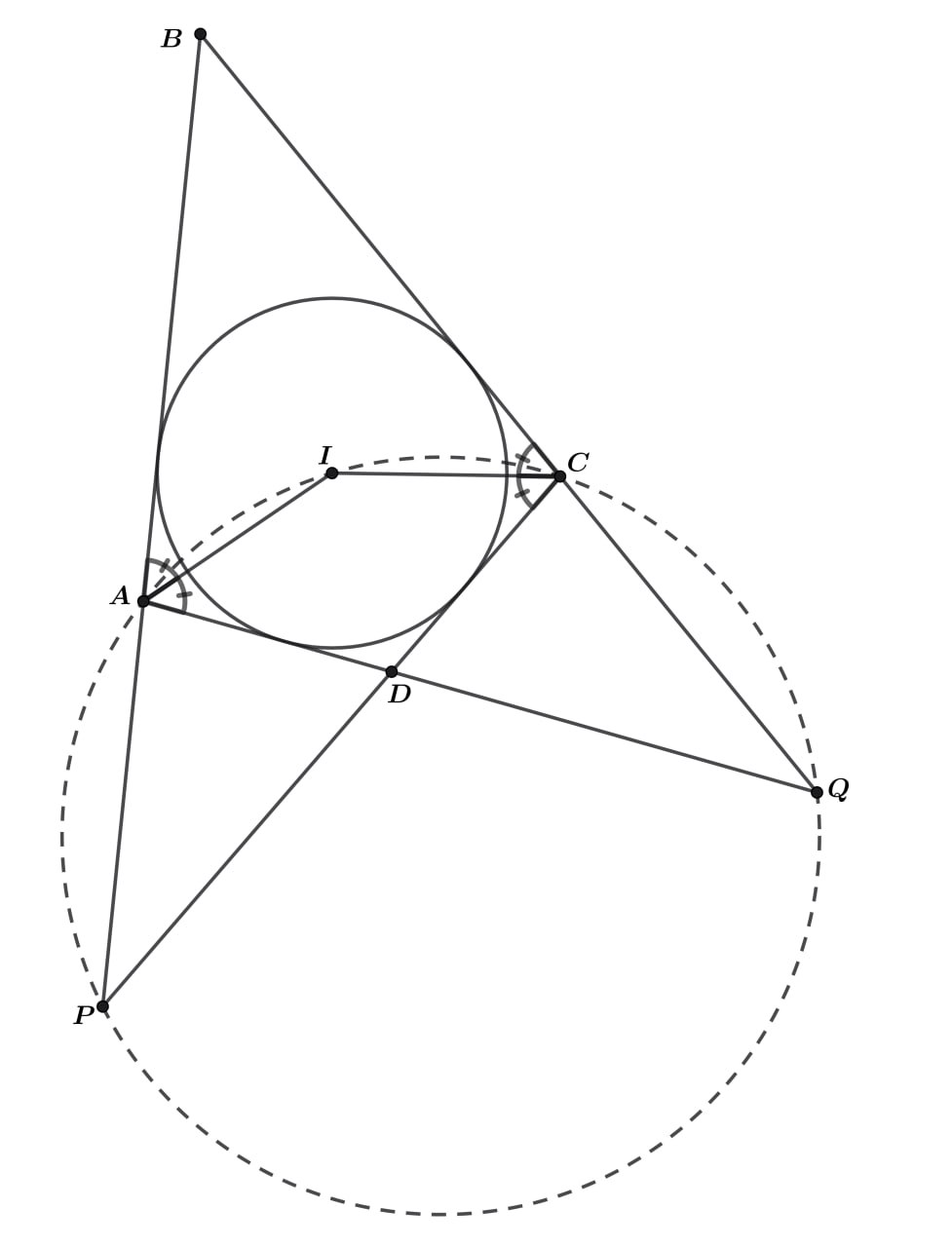
Так как четырёхугольник $AICP$ вписанный, то $∠DCI = ∠PCI = ∠BAI.$ Центр $I$ вписанной окружности четырёхугольника лежит на биссектрисах его углов, поэтому $∠DAI = ∠BAI = ∠DCI = ∠BCI,$ а значит, $∠QAI = ∠BCI = 180∘− ∠QCI.$ Следовательно, точка $Q$ лежит на окружности $ω,$ проходящей через точки $A,I$ и $C.$