Регион 2024

Рассмотрим равносторонний треугольник со стороной разобьём его на правильные треугольнички со стороной и отметим все вершины этих треугольников; полученную конструкцию назовём -треугольником. В дальнейшем под прямыми мы всегда будем понимать прямые, параллельные сторонам этого треугольника и проходящие через хотя бы одну отмеченную точку.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Пусть — отмеченная точка в -треугольнике. Тогда существует единственный способ провести прямых так, что все отмеченные точки, кроме, возможно, покрыты этими прямыми. А именно, для каждой стороны -треугольника надо провести все прямые, параллельные ей и лежащие между этой стороной и точкой включая саму сторону, но исключая прямую, содержащую

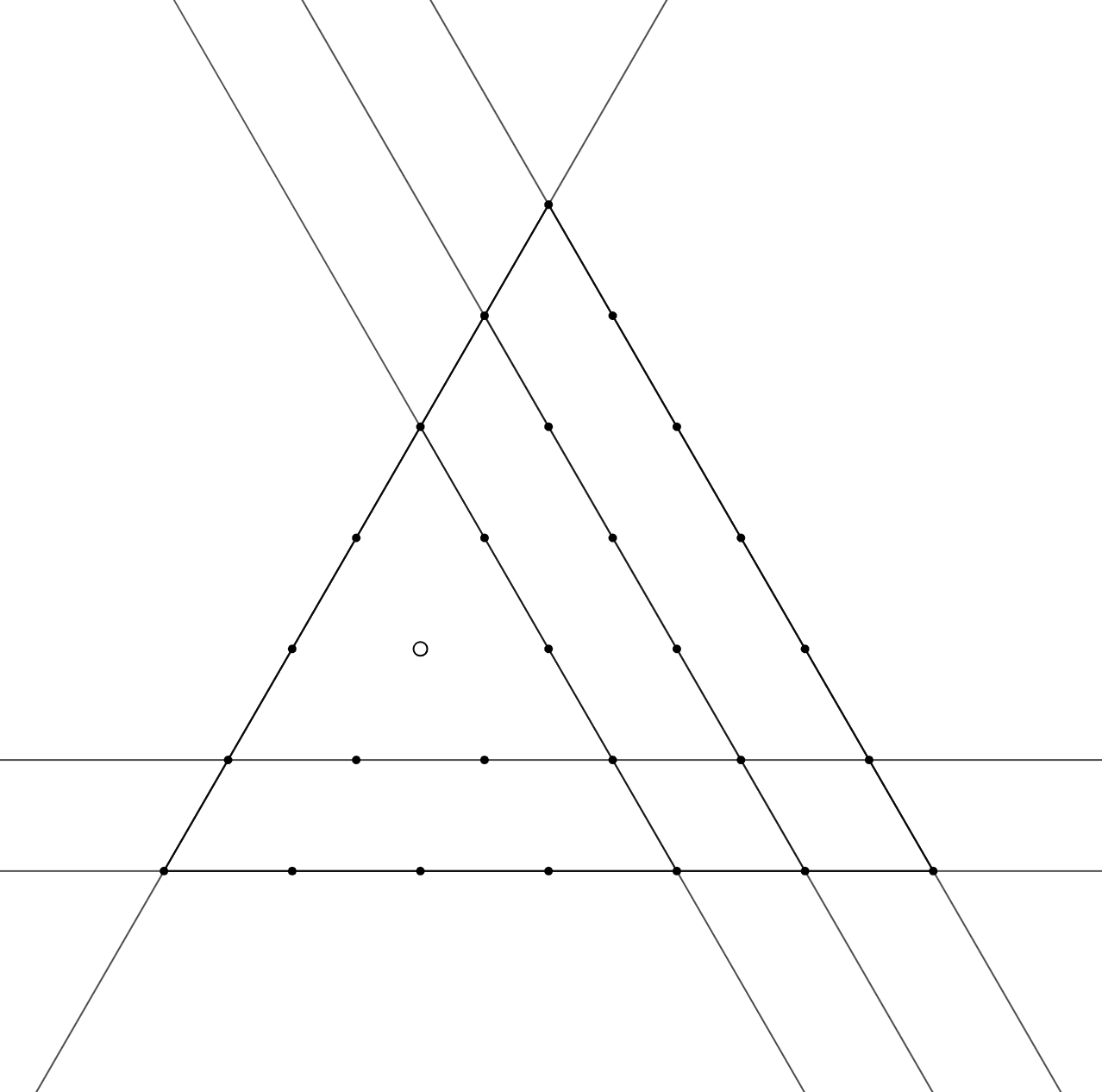
Доказательство. Индукция по База при проверяется легко: надо провести прямую, содержащую две оставшихся точки, кроме

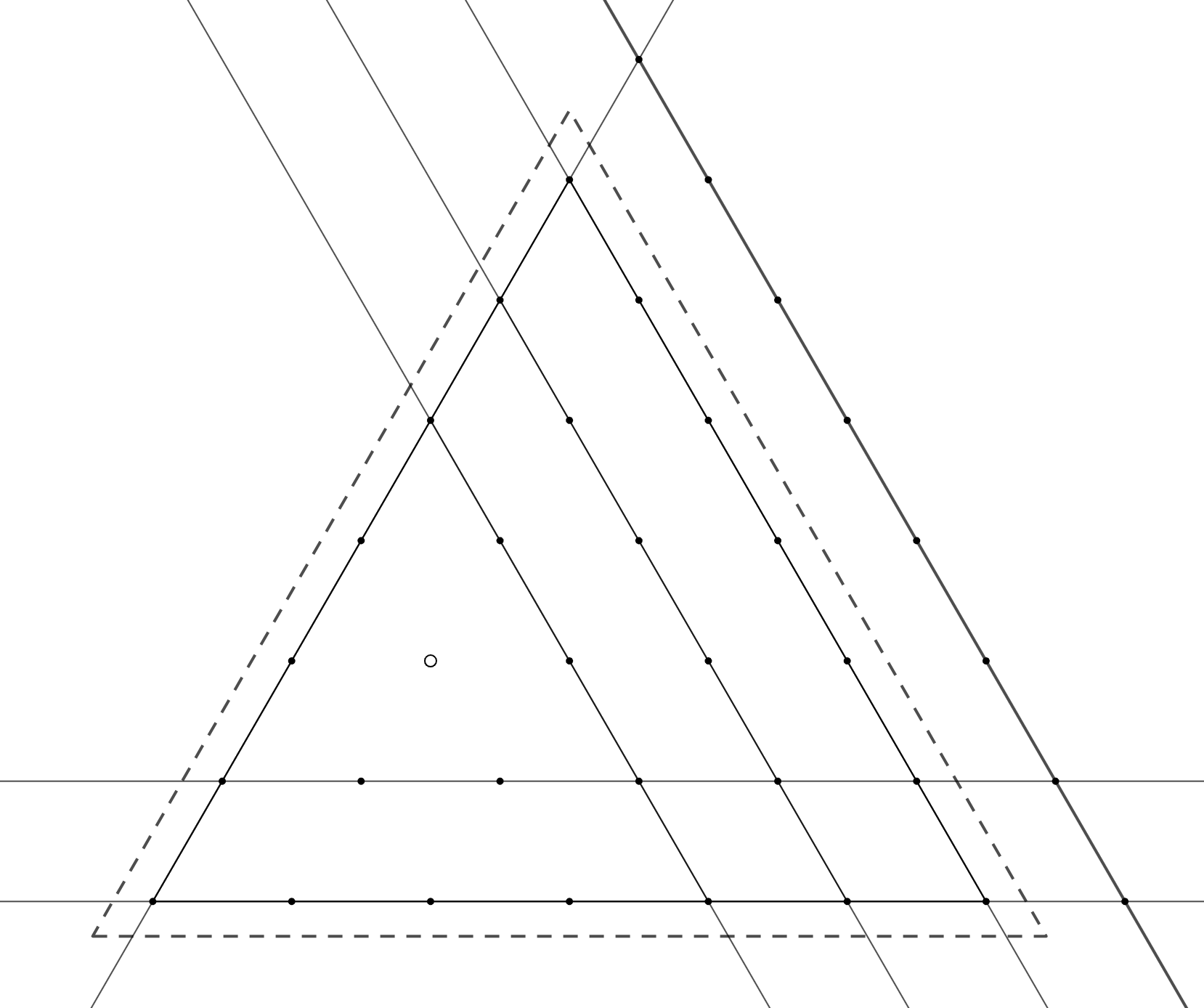
Для перехода рассмотрим сторону -треугольника, на которой не лежит Если прямая, содержащая эту сторону, не проведена, то все отмеченных точек на этой прямой должны быть покрыты различными прямыми; это невозможно, так как прямых Значит, эта прямая проведена. Выкинув её и точки -треугольника, лежащие на ней, получаем -треугольник, в котором проведено прямых с теми же условиями. Осталось применять предположение индукции.

_________________________________________________________________________________________________________________________________________________________________________________

Перейдём к задаче. Рассмотрим одно из разбиений на линейные множества. Для каждого множества проведём прямую, его содержащую. Тогда эти прямые покрыли все отмеченные точки -треугольника, кроме, возможно, его центра Значит, эти прямые устроены так, как описано в лемме, и для любого разбиения этот набор прямых один и тот же.

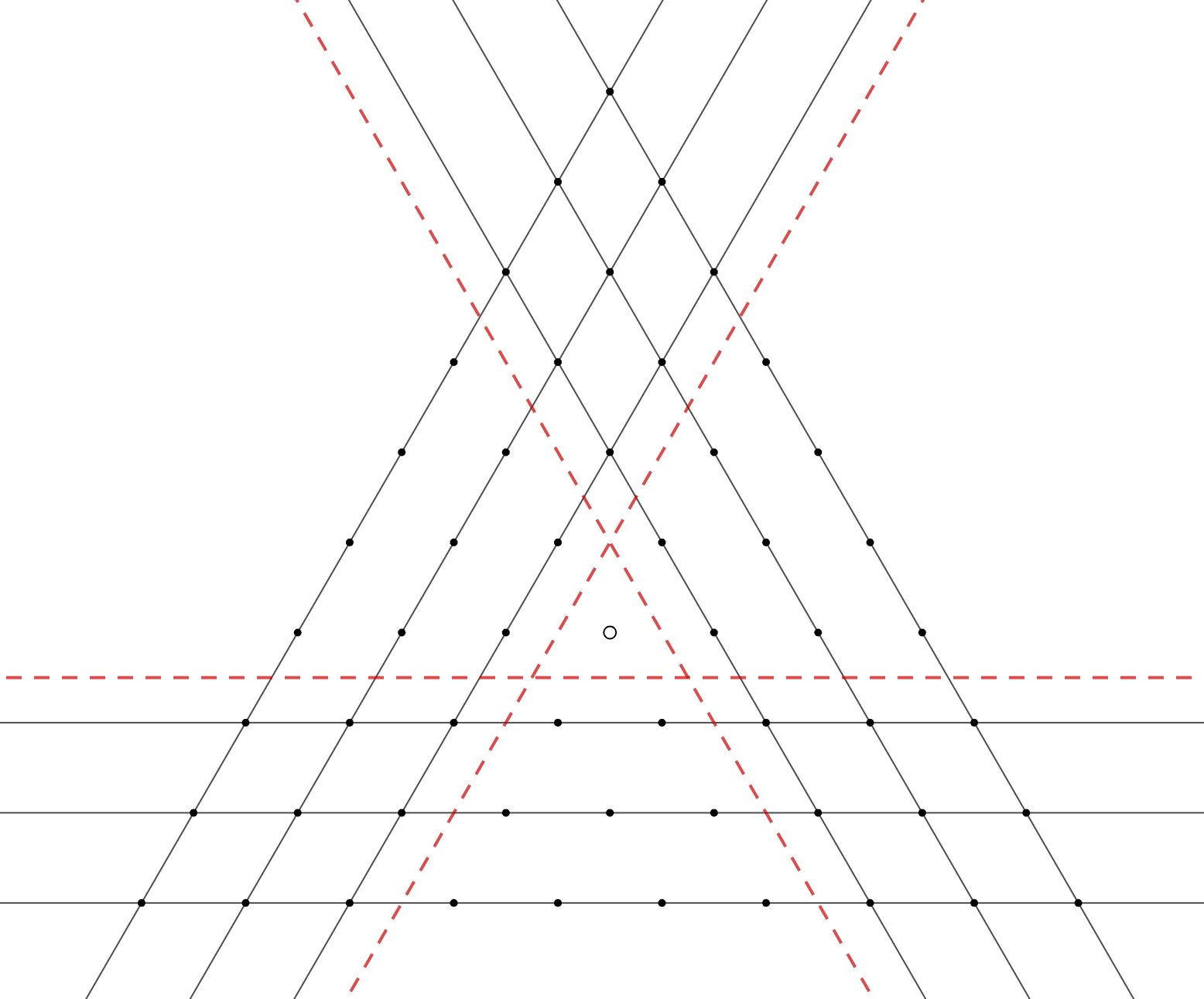
Заметим, что наш -треугольник разбился на областей: три «ромба» в углах, состоящих из точек, покрытых нашими прямыми дважды, и три «трапеции» у сторон, в которых каждая точка покрыты одной прямой. Тогда каждая точка в «трапеции» относится к множеству, лежащему на этой прямой; каждую же точку в «ромбе» можно отнести к любому из двух множеств, лежащих на проходящих через неё прямых. Все такие выборы можно сделать независимо друг от друга. Поскольку в каждом из трёх «ромбов» всего точек, получаем, что требуемых разбиений ровно