Регион 2024
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
График квадратного трехчлена
с вещественными коэффициентами пересекает график
квадратного трехчлена
в точках
и
Касательные в точках
и
к графику
пересекаются в
точке
Оказалось, что точка
лежит на графике
Найдите все возможные значения
Источники:
Подсказка 1
Вычтем из обоих трехчленов линейную функцию, проходящую через A и B. Как теперь выглядят условия задачи?
Подсказка 2
На самом деле, условия касания парабол и прямых, а также пересечение прямых на параболе сохраняются и для новых трехчленов. Осталось решить задачу для более простого случая, когда параболы пересекаются в 2 точках, являющиеся из нулями.
Вычтем из обоих трехчленов линейную функцию, график которой проходит через точки и
Обозначим
полученные трехчлены соответственно
и
(где у
старший коэффициент равен
а у
он равен
). Пусть абсциссы точек
и
равны соответственно
и
Тогда
и
касательные в точках
и
к графику трехчлена
пересекаются на графике
В самом деле,
вычитание линейной функции сохраняет условия касания прямой и параболы в точке с заданной абсциссой, а также
пересечения двух прямых и параболы в одной точке.
Обозначим через
Поскольку
график трехчлена
симметричен
относительно прямой
поэтому касательные к этому графику в точках
и
пересекаются на оси
симметрии. Пусть также точка пересечения касательных имеет координаты
а вершина параболы-графика
имеет координаты
Поскольку старший коэффициент трехчлена равен
имеет место равенство
или
поскольку график
есть парабола
, перенесенная параллельно так, чтобы вершина
попала в
По этой же причине угловые коэффициенты касательных в точках
и
есть
значит,
Таким образом, если перенести параболы-графики
и
так, чтобы
их вершины попали в
то ординаты точек с абсциссой
на этих параболах будут соответственно
и
из чего следует, что старший коэффициент у
в
раза больше, чем у
Ошибка.
Попробуйте повторить позже
У Олега есть набор из 2024 различных клетчатых прямоугольников размеров
…,
(по одному прямоугольнику
каждого размера). Может ли он, выбрав некоторые из них, составить какой-нибудь клетчатый квадрат площадью больше
1?
Источники:
Подсказка 1:
Предположим, что это возможно. Пусть n — наибольшая из длин выбранных прямоугольников. Попробуйте как-нибудь оценить площадь квадрата.
Подсказка 2:
Например, ясно, что его площадь не меньше n², поскольку сторона не меньше n. Возможно, можно найти какое-то противоречие с этим?
Подсказка 3:
Какой может быть наибольшая площадь выбранных прямоугольников?
Предположим противное, и пусть — наибольшая из длин выбранных прямоугольников. Тогда составлен клетчатый квадрат
где
Значит, его площадь не менее
С другой стороны, его площадь не больше, чем суммарная площадь всех
прямоугольников
то есть не больше
Противоречие.
не сможет
Ошибка.
Попробуйте повторить позже
По кругу стоят 100 белых точек. Аня и Боря красят по очереди по одной ещё не покрашенной точке в красный или синий цвет, начинает Аня. Аня хочет, чтобы в итоге оказалось как можно больше пар разноцветных соседних точек, а Боря — чтобы оказалось как можно меньше таких пар. Какое наибольшее число пар разноцветных соседних точек Аня может гарантировать себе независимо от игры Бори?
Источники:
Подсказка 1:
Попробуйте рассмотреть простую стратегию (она будет одинаковой для обоих игроков).
Подсказка 2:
Пусть Аня на каждом ходу ищет пару из неокрашенной и окрашенной точки, красит неокрашенную в противоположный цвет. Сколько пар она сможет создать?
Подсказка 3:
Учтите, что в конце игры количество разноцветных пар должно быть чётным. Почему это так?
Подсказка 4:
Стратегия Бори аналогична. Почему он не позволит Ане создать более 50 пар?
Нужно показать, что Аня всегда может добиться, чтобы разноцветных пар было не меньше 50, а Боря сможет помешать ей добиться, чтобы таких пар было больше 50.
Аня красит в любой цвет любую точку, а дальше каждым ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной (такая, очевидно, найдётся), и красит непокрашенную точку в цвет, отличный от цвета покрашенной. При этом образуется новая пара соседних разноцветных точек.
Боря каждым своим ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной, и красит непокрашенную точку в цвет, совпадающий с цветом покрашенной. При этом образуется новая пара соседних одноцветных точек.
Всего в круге имеется 100 пар соседних точек, и каждый игрок делает по 50 ходов. В итоге Боря добьётся того, что хотя бы 50 пар будут одноцветными, а Аня — что хотя бы 49 пар будут разноцветными. Однако количество разноцветных пар всегда чётно. Действительно, после окончания игры пройдём полный круг, начиная с какой-либо отмеченной точки (пусть для определённости с красной). Группы из идущих подряд красных и синих точек будут чередоваться: К—С—К—С—…—К, и значит, встретим пар разноцветных соседей вида К—С столько же, сколько пар вида С—К. Поэтому если пар разноцветных соседних точек не меньше 49, то их хотя бы 50.
50
Ошибка.
Попробуйте повторить позже
Пусть — возрастающая последовательность натуральных чисел. При
обозначим
Какое наибольшее количество натуральных чисел может содержаться среди
…,
?
Источники:
Подсказка 1:
Ясно, что pᵢ от pᵢ₋₁ отличается умножением на (xᵢ - 1) / xᵢ. Попробуйте подобрать такое xᵢ, чтобы pᵢ стало натуральным, если известно, что pᵢ₋₁ — натуральное.
Подсказка 2:
Если взять xᵢ = pᵢ₋₁, знаменатель сократится, и pᵢ будет натуральным.
Подсказка 3:
Отсюда следует вывод, что если некоторое pᵢ натуральное, то все следующие тоже можно сделать натуральными. Осталось понять, при каком минимальном индексе pᵢ может быть натуральным.
Число не может быть натуральным. Если
то
если же
то
— не целое. Следовательно,
натуральными могут быть не более 2023 чисел
Можно взять
тогда
При положим
Тогда
и все будут натуральными.
2023
Ошибка.
Попробуйте повторить позже
На отрезке как на диаметре построена полуокружность и выбрана произвольная точка
на этом отрезке. Девять лучей из точки
делят развернутый угол
на 10 равных частей и пересекают полуокружность в точках
…,
соответственно (в порядке
обхода от
к
). Докажите, что сумма площадей треугольников
и
равна площади четырехугольника
Источники:
Подсказка 1.
Подступиться к площадям из условия сложно, в таких задачах зачастую помогает прибавлять и вычитать области из обеих частей, чтобы получить что-то приятное.
Подсказка 2.
Избавимся от площади четырёхугольника и суммы площадей в одной из частей, сведя всё к равенству двух треугольников.
Подсказка 3.
Требуется доказать, что площади треугольников ZA₂A₈ и ZA₃A₇ равны. Какие формулы могут нам помочь?
Подсказка 4.
Сумма углов при вершине Z равна 180°, поэтому хотим доказать, что ZA₂⋅ZA₈=ZA₃⋅ZA₇.
Подсказка 5.
Надо доказать что-то про произведения отрезков, у каждого из которых один конец лежит на окружности. Это напоминает степени точек.
Подсказка 6.
Отразите картинку относительно XY.
Покажем, что Требуемое в условии равенство получается вычитанием из обеих частей этого равенства площади
серого треугольника с вершиной в точке
а также добавлением площадей двух серых треугольников, примыкающих к хордам
и
(см. рис.).
.png)
Заметим, что
поэтому синусы этих углов равны. Поэтому достаточно доказать, что Покажем, что оба произведения равны
Для этого достаточно доказать следующее вспомогательное утверждение.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Пусть и
— две точки на полуокружности с диаметром
точка
лежит на отрезке
и
Тогда
Доказательство. Отметим точку симметричную
относительно
Тогда четырёхугольник
вписан в окружность с
диаметром
Также в силу симметрии
и
то есть точки лежат на одной прямой. Значит,
— точка пересечения диагоналей вписанного четырёхугольника
поэтому
.png)
_________________________________________________________________________________________________________________________________________________________________________________
Таким образом, лемма доказана, что завершает решение задачи.
Ошибка.
Попробуйте повторить позже
Уравнение
имеет положительные решения Докажите, что
Источники:
Обозначим
и перепишем уравнение в виде:
Заметим, что
Дальше, перепишем уравнение в виде
откуда сразу следует, что все его корни строго больше 1. Добавим к каждой части уравнение превратится
в
где
Если обозначить то получим однородное уравнение
из которого следует, что где
Дальше, каждое из уравнений можно переписать в виде
Эти уравнения различны, и каждое из них имеет два различных положительных корня, так как исходное уравнение имеет 4 различных
положительных корня. Из этого следует, что
Так как функция строго убывает при
(это несложно показать, например, взяв производную),
то
Теперь уже легко вычислить и упорядочить :
значит,
Ошибка.
Попробуйте повторить позже
Правильный треугольник со стороной 111 разбит прямыми, параллельными его сторонам, на правильные треугольники со
стороной 1. Все вершины этих треугольников, кроме центра треугольника
отмечены. Назовём множество из нескольких
отмеченных точек линейным, если все эти точки лежат на одной прямой, параллельной стороне
Сколько существует
способов разбить все отмеченные точки на 111 линейных множеств? (Способы, отличающиеся порядком множеств, считаются
одинаковыми.)
Источники:
Рассмотрим равносторонний треугольник со стороной разобьём его на правильные треугольнички со стороной
и отметим
все вершины этих треугольников; полученную конструкцию назовём
-треугольником. В дальнейшем под прямыми мы
всегда будем понимать прямые, параллельные сторонам этого треугольника и проходящие через хотя бы одну отмеченную
точку.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Пусть — отмеченная точка в
-треугольнике. Тогда существует единственный способ провести
прямых так, что все
отмеченные точки, кроме, возможно,
покрыты этими прямыми. А именно, для каждой стороны
-треугольника надо провести все
прямые, параллельные ей и лежащие между этой стороной и точкой
включая саму сторону, но исключая прямую, содержащую
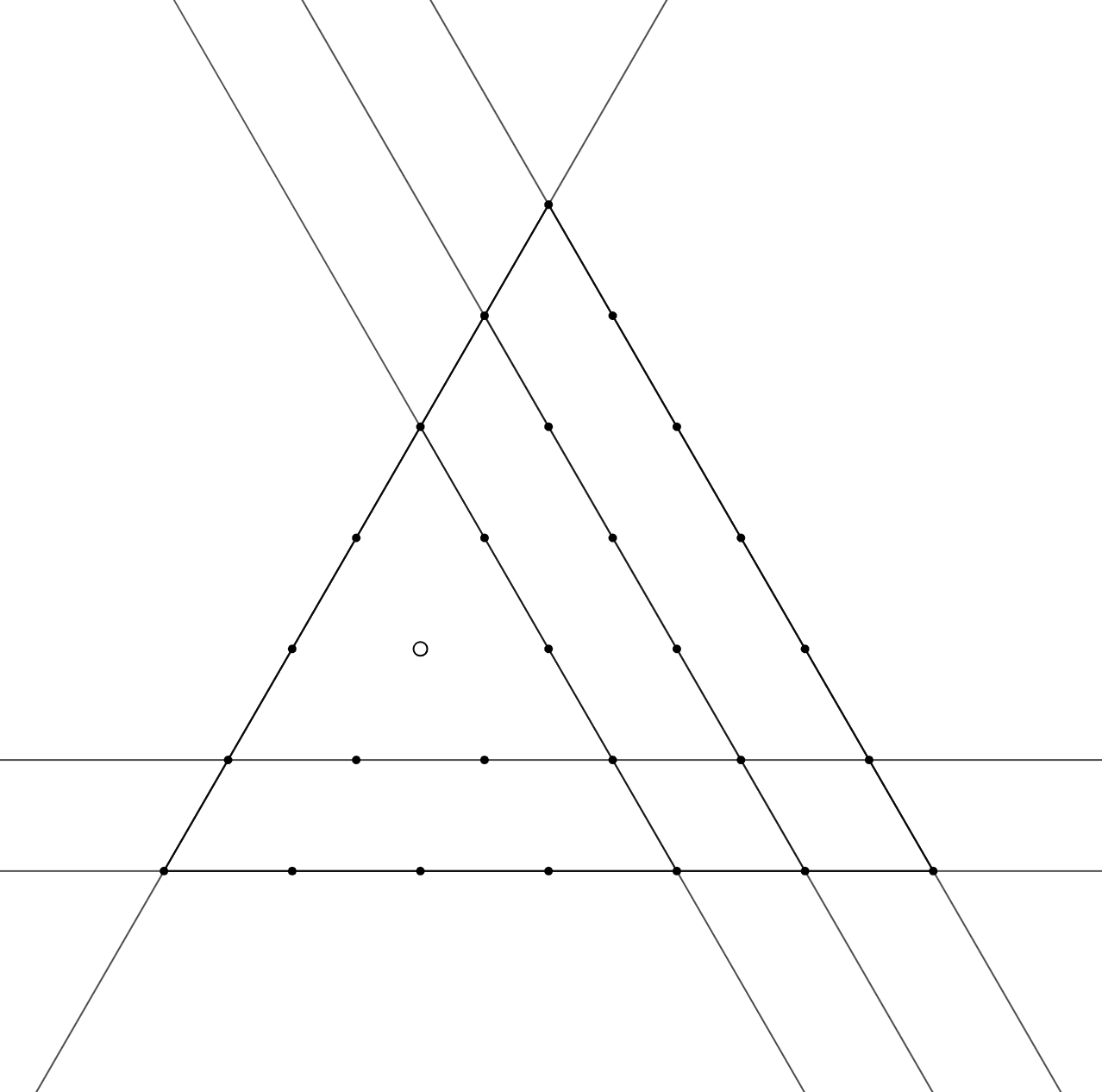
Доказательство. Индукция по База при
проверяется легко: надо провести прямую, содержащую две оставшихся точки,
кроме
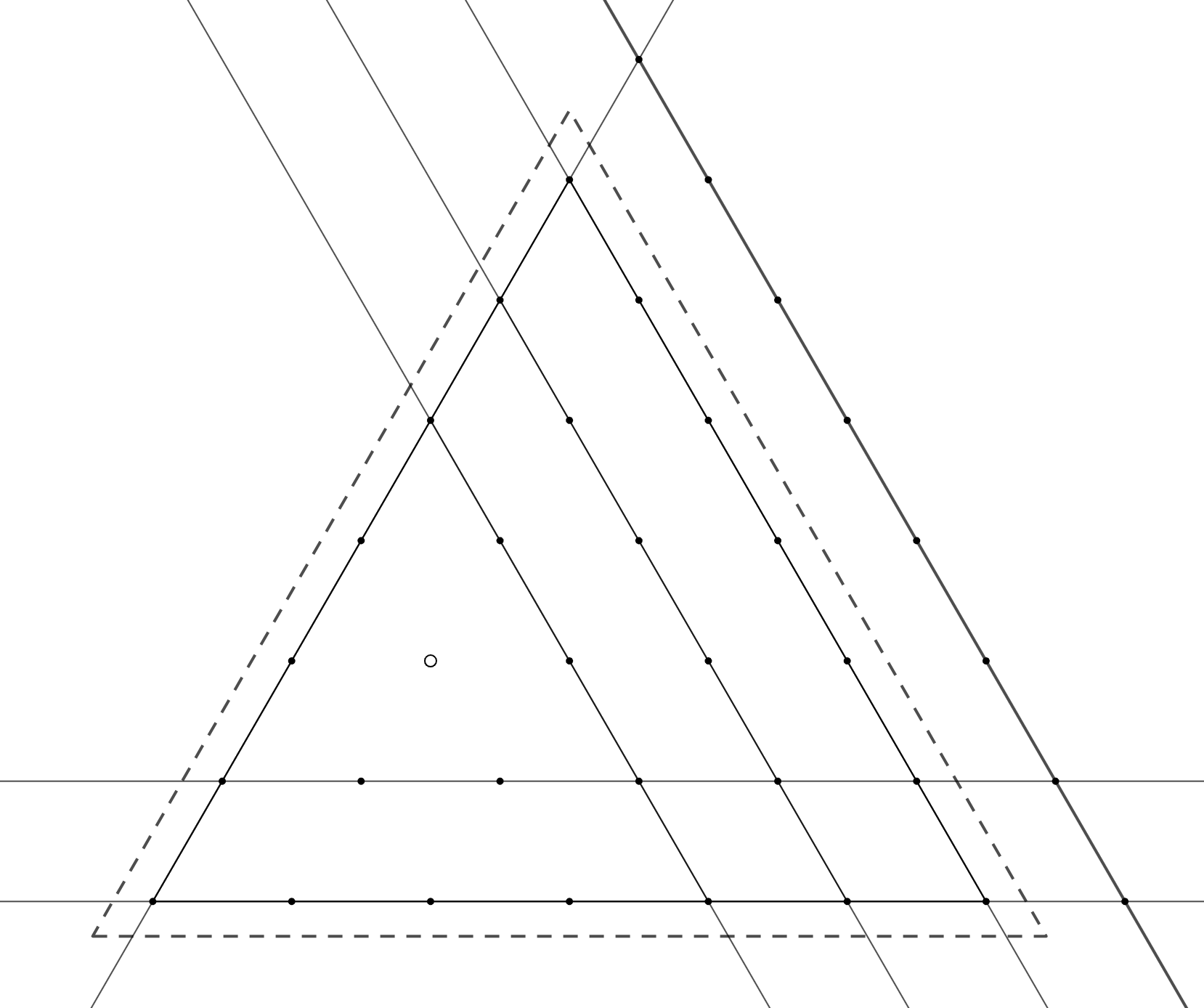
Для перехода рассмотрим сторону -треугольника, на которой не лежит
Если прямая, содержащая эту сторону, не
проведена, то все
отмеченных точек на этой прямой должны быть покрыты различными прямыми; это невозможно,
так как прямых
Значит, эта прямая проведена. Выкинув её и точки
-треугольника, лежащие на ней, получаем
-треугольник, в котором проведено
прямых с теми же условиями. Осталось применять предположение
индукции.
_________________________________________________________________________________________________________________________________________________________________________________
Перейдём к задаче. Рассмотрим одно из разбиений на линейные множества. Для каждого множества проведём прямую, его содержащую.
Тогда эти прямые покрыли все отмеченные точки -треугольника, кроме, возможно, его центра
Значит, эти прямые устроены так, как
описано в лемме, и для любого разбиения этот набор прямых один и тот же.
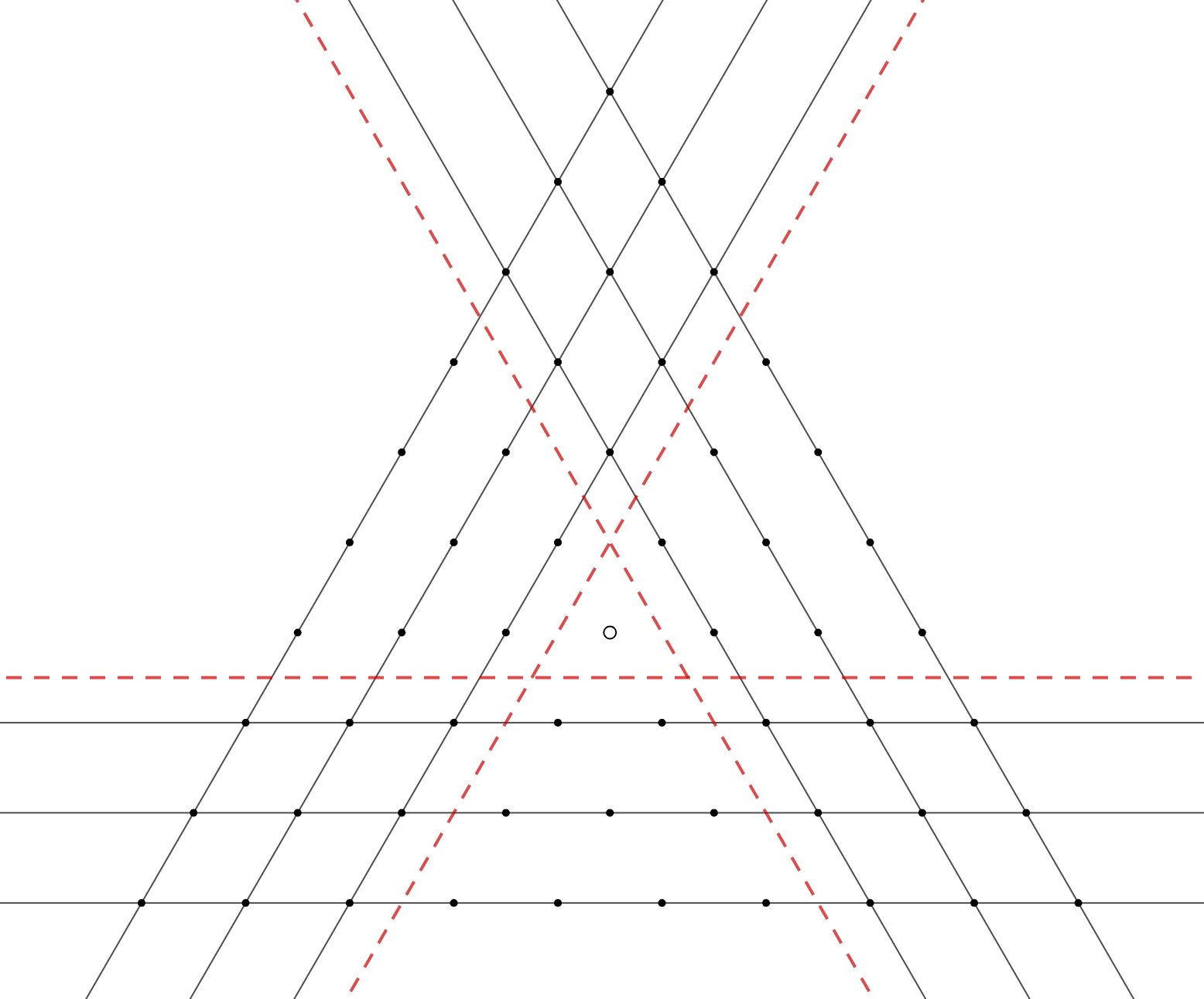
Заметим, что наш -треугольник разбился на
областей: три «ромба» в углах, состоящих из точек, покрытых нашими прямыми
дважды, и три «трапеции» у сторон, в которых каждая точка покрыты одной прямой. Тогда каждая точка в «трапеции» относится к
множеству, лежащему на этой прямой; каждую же точку в «ромбе» можно отнести к любому из двух множеств, лежащих на проходящих
через неё прямых. Все такие выборы можно сделать независимо друг от друга. Поскольку в каждом из трёх «ромбов» всего
точек,
получаем, что требуемых разбиений ровно
Ошибка.
Попробуйте повторить позже
У учителя есть 100 гирь массами 1 г, 2 г, …, 100 г. Он хочет раздать Пете и Васе по 30 гирь так, чтобы выполнялось следующее условие: никакие 11 Петиных гирь не уравновешиваются никакими 12 Васиными гирями, а также никакие 11 Васиных гирь не уравновешиваются никакими 12 Петиными гирями. Сможет ли учитель это сделать?
Источники:
Первое решение. Выберем гирь с массами вида
и дадим Пете, а Васе дадим
гирь с массами вида
г. Тогда масса
любых
гирь, взятых у одного человека, будет делиться на
а масса любых
гирь, взятых у одного человека, не будет делиться на
______________________________________________________________________________________________________________________________________________________
Второе решение. Выберем гирь с массами
и дадим Пете, а Васе дадим
гирь с массами
г.
Тогда у Пети масса любых 11 или 12 гирь будет меньше
г. А масса любых
или
гирь у Васи будет больше
г.
сможет
Ошибка.
Попробуйте повторить позже
В пространстве расположены отрезки
и
с общей серединой
Оказалось, что сфера
описанная около тетраэдра
касается плоскости
в точке
Точка
— центр окружности, описанной около треугольника
Докажите, что
Источники:
Подсказка 1
Каким способом можно доказывать равенство двух отрезков? Может, стоит найти третий отрезок, который будет равен одному из иcходных?
Подсказка 2
Действительно, у нас уже есть пары равных отрезков AM и A'M, BM и B'M, CM и C'M. В частности, это говорит о том, что треугольники ABC и A'B'C' симметричны относительно точки M. Как построить отрезок, равный OM, связь которого со сферой была бы более естественна, чем та же у последнего?
Подсказка 3
Если O' — центр описанной окружности треугольника A'B'C', то OM=M'O. Как эти точки связаны с D?
Подсказка 4
На самом деле, касание сферы и плоскости влечет равенство угла ODO' прямому. Осталось понять, чем является точка M в треугольнике ODO'.
Обозначим через центр окружности, описанной около треугольника
через
— центр сферы
(см. рис.). При центральной
симметрии относительно точки
треугольник
переходит в треугольник
Следовательно, точки
и
симметричны
относительно точки
то есть
— середина отрезка
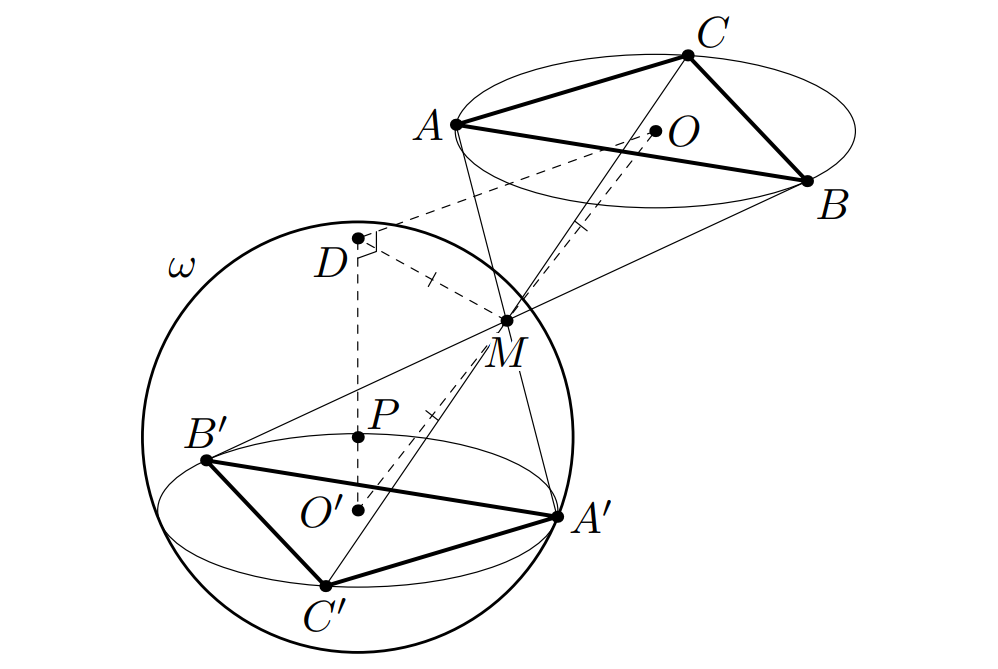
Также мы получаем, что плоскости и
параллельны. Тогда на прямой, проходящей через точку
перпендикулярно этим
плоскостям, лежат точки
и
поэтому
Таким образом,
— медиана в прямоугольном треугольнике
значит,
что и требовалось.
Ошибка.
Попробуйте повторить позже
Дано натуральное число Изначально на доске написано число 1. Каждую минуту Петя представляет число, записанное на доске, в
виде суммы двух неравных положительных несократимых дробей, а Вася оставляет на доске только одну из этих двух дробей. Докажите,
что Петя может добиться того, чтобы знаменатель оставшейся дроби через
минут не превышал
вне зависимости от действий
Васи.
Источники:
Подсказка 1
Рассмотрим разбиение числа 1 в сумму 2ⁿ различных несократимых дробей вида 1/mᵢ, где mᵢ ≤ 2ⁿ + 50. Можно ли из такого разбиения получить стратегию игры для Пети?
Подсказка 2
Построим двоичное дерево глубины n, где в листьях — эти дроби, а в корне — 1. Каждая внутренняя вершина — сумма двух потомков. При каких условиях это дерево можно использовать в качестве стратегии и гарантирует ли оно нужный результат независимо от выборов Васи?
Подсказка 3
Для построения дерева необходимо, чтобы на каждом уровне при разбиении суммы на два слагаемых эти слагаемые были различны. Возможно, есть способ производить построение дерева снизу вверх, сразу для большого числа чисел, например, перемешивая две четверки различных чисел.
Подсказка 4
Докажите ключевую лемму: если есть две четверки попарно различных чисел, их можно разбить на четыре пары (по одному числу из каждой четверки) так, чтобы: числа в парах были различны, суммы пар были различны. Попробуйте доказать разбором случаев, учитывая возможные равенства между четверками.
Подсказка 5
При каких условиях на начальные 2ⁿ дробей можно воспользоваться данной леммой для построения дерева? Очевидно, что среди начальных дробей должно быть хотя бы 4 различных вида дробей, и каждого из них не более 2ⁿ⁻² штук.
Подсказка 6
Очевидный способ для одного представления: возьмите 2ⁿ⁻² дробей вида 1/2ⁿ. Может, поискать представления так же вида 1/m?
Подсказка 7
Для иных представлений: зафиксируем k, где n−k — составное и не степень двойки. Какими k для этих целей можно ограничиться? В этом случае n−k = pt, где t > 1 и нечетно. Правда ли, что тогда 2ⁿ⁻ᵏ + 1 делится на 2ᵖ?
Подсказка 8
Можно ли представить ¼ в виде суммы дробей 1/(2ⁿ + 2ᵏ) и (2ᵏ⁺ᵖ+2ᵏ)/2ᵏ⁺ᵖ·(2ⁿ + 2ᵏ) в правильных пропорциях?
Построим двоичное дерево глубины со значениями в вершинах, следующим образом: представим
в виде суммы
дробей с
числителями
и знаменателями, не превосходящими
поместим данные дроби в листьях; значения остальных вершин это сумма
их потомков (следовательно в корне будет
). Если у каждой вершины (кроме, разумеется, листьев) значения потомков различны, то такое
дерево соответствует победной стратегии Пети: каждое число из дерева записывается в виде суммы значений потомков, а Вася, выбирая
одно из них, осуществляет спуск по дереву. Через
минут они спустятся в один из листов, то есть будет записана одна из исходных
дробей.
Теперь покажем, что такое дерево существует, для этого докажем лемму.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Есть 2 четвёрки чисел
Тогда их можно сгруппировать по парам чтобы числа в каждой паре были различны и суммы чисел в каждой паре были
различны.
Доказательство. Разберем несколько случаев:
Если
не умаляя общности
и можно сгруппировать
В случае и н.у.о.
группируем
сводится к предыдущему, если мы перейдем к четверкам чисел
Пары
и
разные, а также пары
и
разные. В таком случае покажем как сгруппировать числа
первых двух пар между собой, с числами в третьей и четвертой паре поступим аналогично, явно получив две меньшие суммы чем в первой
паре. Если
или
подходит
в противном случае можно сгруппировать
и
Покажем, что описанное в начале решения дерево существует (значения потомков на каждом шаге — различные числа),
если исходные дробей удастся разбить на четверки так, чтобы в каждой четверке были попарно различные дроби.
Действительно, в таком случае на очередном шаге мы разобьем четверки на пары и согласно лемме будем складывать числа из
разных четверок. После каждого такого шага получившиеся суммы вновь будут разбиваться на четверки попарно различных
чисел.
_________________________________________________________________________________________________________________________________________________________________________________
Построив снизу вверх так первые уровня дерева, мы в итоге получим четверку различных чисел
далее рассмотрим вершины со значениями(и соответствующими потомками) и
и последнем шаге сложим уже эти два
числа, получив
в корне.
Таким образом, достаточно представить в виде суммы
дробей вида
четырьмя разными способами, каждый раз
используя разные знаменатели, не превосходящие
Первый способ — сумма одинаковых дробей
Построим три других представления. Заметим, что среди
чисел
не более одной степени двойки и не более двух простых чисел (потому что простые числа, большие трех, могут давать только
остатки 1 и 5 от деления на 6), уберем такие числа из рассмотрения. Любое оставшееся число можно представить в виде
где
и
нечетно. Тогда
кратно
обозначим частное от деления через
Получаем,
что
Возьмем дроби вида
и
дроби вида
Поскольку
то
Посчитаем сумму этих дробей:
Проделаем так для трех различных значений остается убедиться, что полученные представления не содержат одинаковых дробей.
Ясно, что с первым выбранным набором три новых не пересекаются, а также дроби вида
могут быть лишь в одном наборе.
Остается проверить, что дроби вида
различны. Предположим противное,
Поскольку
и
нечетны,
получаем, что
и это число — общий делитель
и
Тогда
кратно
поэтому
Однако,
откуда и
противоречие.


