Регион 2022
Ошибка.
Попробуйте повторить позже
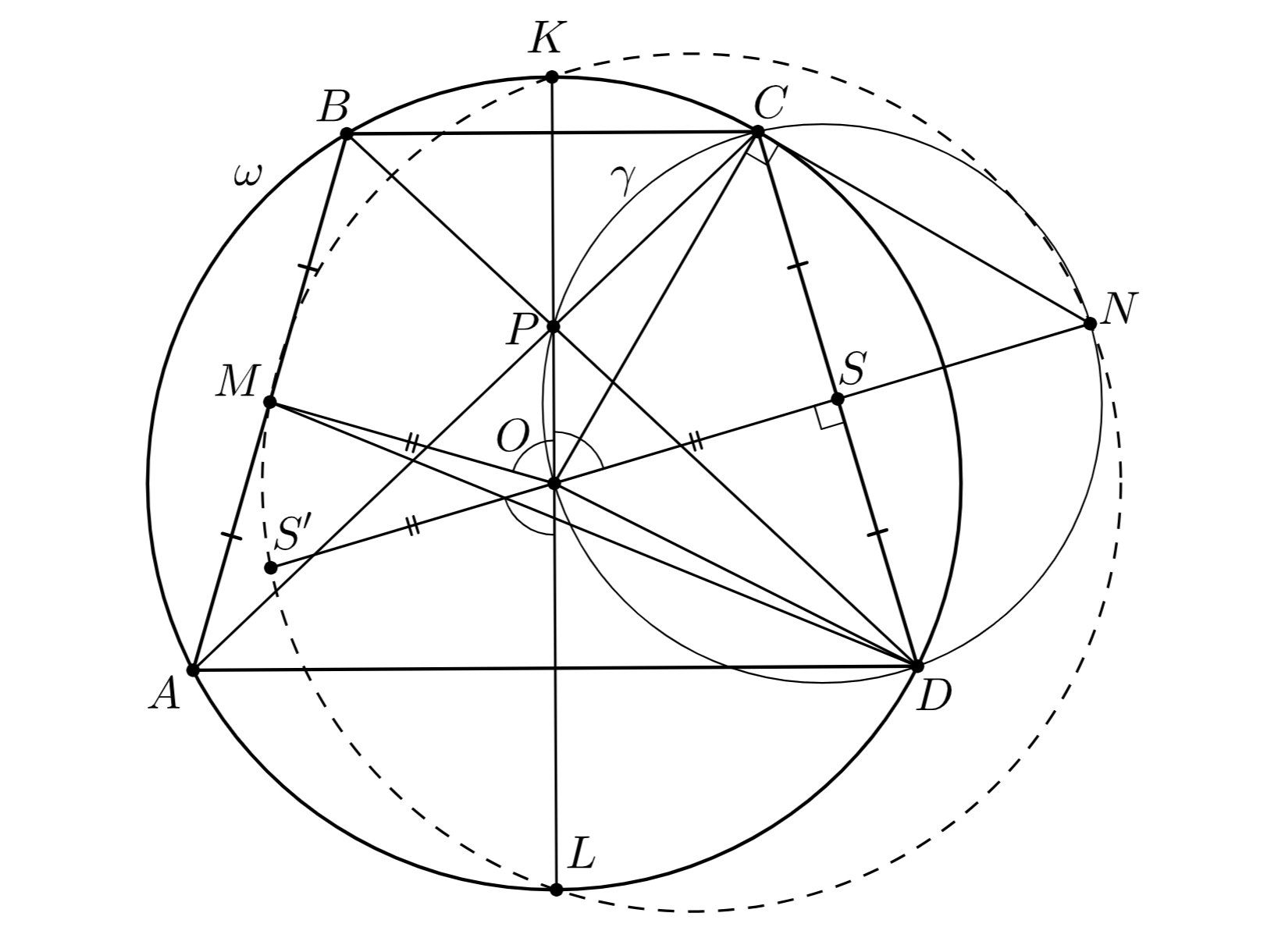
Трапеция с основаниями
и
вписана в окружность
Диагонали
и
пересекаются в точке
Точка
— середина отрезка
Серединный перпендикуляр к отрезку
пересекает окружность
в точках
и
Точка
—
середина дуги
описанной окружности треугольника
не содержащей точку
. Докажите, что точки
и
лежат
на одной окружности.
Обозначим через центр окружности, описанной около трапеции
Тогда
Здесь мы воспользовались тем, что центральный угол вдвое больше вписанного, и что внешний угол треугольника равен сумме двух внутренних, с ним не смежных.
Следовательно, точка лежит на окружности
описанной около треугольника
и поскольку
то
— середина
дуги
Тогда отрезок
— диаметр окружности
а прямая
— серединный перпендикуляр к отрезку
В частности,
середина отрезка
обозначим её через
лежит на отрезке
Из сказанного выше,
Значит, окружность, описанная около треугольника касается прямой
поэтому
Отметим точку симметричную точке
относительно точки
Тогда
поэтому точки лежат на одной окружности.
Теперь заметим, что точки и
симметричны относительно прямой
Значит,
Таким образом, точки и
симметричны относительно серединного перпендикуляра к
Следовательно, точки
и
лежат на одной окружности. Из сказанного выше, на этой окружности лежит также и точка
что и
требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




