Тема Регион 11 класс

Регион 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 11 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80578Максимум баллов за задание: 7

Даны неотрицательные числа $a,b,c,d$ такие, что $a+ b+ c+d =8.$ Докажите, что

---a3--- --b3--- ---c3--- --d3---- a2+ b+ c + b2 +c+ d + c2+ d+a + d2+a +b ≥ 4

Источники: Всеросс., 2022, РЭ, 11.10(см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Знаменатель каждой дроби можно оценить хорошо по неравенству о средних, но пока знак не в ту сторону. Попробуйте выделить целую часть в дроби так, чтобы она стала с минусом.

Подсказка 2

Запишем a³/(a² + b + c), как a - a(b + c)/(a² + b + c). Какое неравенство получится, если оценить знаменатель каждой дроби по неравенству о средних?

Подсказка 3

Верно! Получаем после преобразований неравенство √(a+b) + √(b +c) + √(c + d) + √(a + d) ≤ 8. Попробуйте сгруппировать естественным образом слагаемые и каждое из них оценить. Не забывайте, что a + b + c + d = 8!

Показать доказательство

Заметим, что

a3 a(b +c) a(b+c) √b-+c- a2+b+-c = a− a2+-b+-c ≥ a− 2a√b-+c-=a −-2-

Здесь мы оценили знаменатель по неравенству о средних:

a2+b+ c> 2a√b+-c

Сложим полученное неравенство с тремя аналогичными. Теперь нам достаточно доказать, что

√---- √ ---- √---- √---- a+ b+c+ d− -a-+b −--b+c − -c+-d− -d+-a-≥4 2 2 2 2

Поскольку $a+ b+ c+d =8,$ это равносильно неравенству

√---- √---- √---- √ ---- -a+-b+ -b+-c+ -c-+d +--d+-a≤ 4 2 2 2 2

Но из неравенства между средним арифметическим и среднем квадратичным мы получаем, что

∘ ----------------- √a+-b √c-+d- (√a+-b)2-+(√c+-d)2 2 + 2 ≤ 2 =2

и, аналогично,

√---- √---- -b+-c+ -a-+d-≤2 2 2

Складывая эти два неравенства, получаем требуемое.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#88689Максимум баллов за задание: 7

Дан квадратный трехчлен $P (x)$ . Докажите, что существуют попарно различные числа $a$ , $b$ и $c$ такие, что выполняются равенства

P(b+c)= P(a),P(c+ a)= P(b),P (a +b)= P(c).

Источники: ВСОШ, РЭ, 2022, 10.2 и 11.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Очень полезно уметь представлять такие задачи. Мы знаем, что Р(х) --- это трёхчлен. Как выглядит его график?

Подсказка 2

Это парабола! Вспомним, что парабола симметрична относительно некоторой вертикальной прямой. А если значения в двух различных точках параболы равны, то что можно сказать про эти точки?

Подсказка 3

Они равноудалены от абсциссы вершины параболы! Теперь подумайте, чему равна сумма таких точек, и из этого приведите пример к задаче.

Показать доказательство

Пусть $d$ — абсцисса вершины параболы $y =P(x)$ , так что прямая $x= d$ — ось симметрии параболы. Тогда для любых чисел $t$ и $s$ с суммой $2d$ (т.е. таких, что точки $t$ и $s$ симметричны относительно $d)$ выполнено $P(t)= P(s)$ .

Таким образом, любая тройка попарно различных чисел $a,b,c$ с суммой $2d$ будет удовлетворять условию задачи. Можно взять, скажем,

2d 2d 2d a =-3 − 1,b= 3-,c= 3-+1.

Ошибка.
Попробуйте повторить позже

Задача 3#102031Максимум баллов за задание: 7

В треугольной пирамиде $ABCD$ на ее гранях $BCD$ и $ACD$ нашлись соответственно точки $A′$ и $B ′$ такие, что

′ ′ ′ ′ ∘ ∠AB C = ∠AB D = ∠BA C =∠BA D= 120

Известно, что прямые $AA′$ и $BB′$ пересекаются. Докажите, что точки $A′$ и $B ′$ равноудалены от прямой $CD.$

Подсказки к задаче

Подсказка 1

Условие что прямые пересекаются полезно трактовать так: точки A, A’, B, B’ лежат в одной плоскости. Почему это полезно? Дело в том, что прямые BA’, AB’ и CD пересекаются в одной точке. Мы пока не пользовались большей частью условия. Как его связать с замеченным нами фактом?

Подсказка 2

В задаче нужно доказать равноудаленность, значит, имеет смысл поискать какие-то биссектрисы. Сделайте это, а еще на картинке есть разные углы, тогда может быть есть и подобие.

Показать доказательство

Из условия задачи следует, что точки $A,$ $A′,$ $B,$ $B ′$ лежат в одной плоскости, поэтому прямые $BA ′$ и $AB ′$ пересекают ребро $CD$ в одной точке $X.$

$PIC$

Из условия следует, что эти прямые являются биссектрисами углов $CA′D,$ $CB ′D$ соответственно. Отсюда, по свойству биссектрисы,

CA-′= CX- =-CB′ A ′D XD B ′D

а поскольку $∠CA ′D = ∠CB′D =120∘,$ треугольники $CA ′D$ и $CB′D$ подобны. Поскольку $CD$ — общая сторона этих треугольников, эти треугольники равны. В этих равных треугольниках равны соответствующие высоты из вершин $A′$ и $B′.$ Это и требовалось доказать.

Ошибка.
Попробуйте повторить позже

Задача 4#134306Максимум баллов за задание: 7

Петя написал на доске десять натуральных чисел, среди которых нет двух равных. Известно, что из этих десяти чисел можно выбрать три числа, делящихся на 5. Также известно, что из написанных десяти чисел можно выбрать четыре числа, делящихся на 4. Может ли сумма всех написанных на доске чисел быть меньше 75?

Источники: ВСОШ, РЭ, 2022, 9.1, 10.1 и 11.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать пример таких чисел.

Подсказка 2:

Добавьте в набор число 20. Оно одновременно делится на 4 и на 5. Осталось взять два маленьких числа, кратных 5, и три числа, кратных 4.

Показать ответ и решение

Пример: $1,$ $2,$ $3,$ $4,$ $5,$ $6,$ $8,$ $10,$ $12,$ $20.$ В этом наборе три числа $(5,10,20)$ делятся на 5, четыре числа $(4,8,12,20)$ делятся на 4, а общая сумма равна $71.$

Ответ:

может

Ошибка.
Попробуйте повторить позже

Задача 5#134328Максимум баллов за задание: 7

В компании некоторые пары людей дружат (если $A$ дружит с $B,$ то и $B$ дружит с $A$ ). Оказалось, что при любом выборе 101 человека из этой компании количество пар дружащих людей среди них нечётно. Найдите наибольшее возможное количество человек в такой компании.

Источники: ВСОШ, РЭ, 2022, 11.4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать какой-нибудь простой пример и далее уже строить оценку.

Подсказка 2:

Существует пример на 102. Придумайте его. Чтобы показать, что при большем количестве условие не выполняется, достаточно доказать это для 103 человек.

Подсказка 3:

Чтобы это доказать, попробуйте рассмотреть всевозможные варианты удаления двух вершин из графа на 103 вершинах. Пусть при i-м способе в графе осталось aᵢ рёбер. Рассмотрите сумму всех aᵢ, посчитайте её несколькими способами.

Подсказка 4:

На самом деле интересны не конкретные значения, а чётность этой суммы при разных способах подсчёта.

Подсказка 5:

Если доказывать от противного, то все aᵢ нечётные. А что получится, если посчитать, сколько раз каждое ребро учтено в этой сумме?

Показать ответ и решение

Первое решение. Рассмотрим граф дружб, в котором вершины — это люди, а ребро соединяет двух людей, если они дружат. Пусть в компании $102$ человека. Построим граф: одну вершину $x$ соединим с тремя другими $v1,$ $v2,$ $v3.$ Остальные $98$ вершин разобьём на пары и соединим вершины в каждой паре. Всего получаем 52 ребра. При удалении любой вершины исчезает нечётное число рёбер, значит, остаётся также нечётное число. Таким образом, компания из $102$ человек подходит. Покажем, что компаний больше чем из 102 людей быть не может, для этого выберем из них любые 103, достаточно показать, что не существует уже такой компании.

Докажем, что компании из $103$ человек быть не может. Всего способов выбросить две вершины из $103$ равно

n =C2103 = 51⋅103.

Пронумеруем эти способы числами от $1$ до $n$ и пусть $ai$ — количество рёбер в оставшихся $101$ вершинах в $i$ -м способе. По условию $ai$ нечётно, значит, нечётна и их сумма $S.$ С другой стороны, каждое ребро учитывается в числе $ai$ тогда и только тогда, когда его вершины не выброшены, то есть выброшена какая-то другая пара. Это происходит $2 k= C101 =50⋅101$ раз. Таким образом, каждое ребро учитывается в $S$ чётное число раз, поэтому $S$ чётно — противоречие.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Рассмотрим граф дружб, в котором вершины — это люди, а ребро соединяет двух людей, если они дружат. Пусть в компании $102$ человека. Построим граф: одну вершину $x$ соединим с тремя другими $v1,v2,v3.$ Остальные $98$ вершин разобьём на пары и соединим вершины в каждой паре. Всего получаем 52 ребра. При удалении любой вершины исчезает нечётное число рёбер, значит, остаётся также нечётное число. Таким образом, компания из $102$ человек подходит. Покажем, что компаний больше чем из 102 людей быть не может, для этого выберем из них любые 103, достаточно показать, что не существует уже такой компании.

Докажем, что компании из $103$ человек быть не может. Назовём вершину чётной, если её степень чётна, и нечётной иначе.

Случай 1. Общее количество рёбер нечётно. Выбрасывая любую пару вершин, мы должны убирать чётное число рёбер (чтобы осталось нечётное число). Если выбрасываем вершины со степенями $d1$ и $d2,$ не соединённые ребром, то $d1+d2$ чётно; если соединены, то $d1+ d2$ нечётно. Следовательно, вершины одинаковой чётности не соединены, а вершины разной чётности соединены. Пусть в графе $k$ чётных вершин, тогда число рёбер равно $k(103 − k)$ — чётно, противоречие.

Случай 2. Общее количество рёбер чётно. Аналогично можно показать, что вершины одинаковой чётности соединены, а вершины разной чётности не соединены. Тогда число отсутствующих рёбер равно $k(103− k),$ то есть общее число рёбер равно

C2103− k(103− k)=103⋅51− k(103− k),

что нечётно. Противоречие.

Ответ:

102

Ошибка.
Попробуйте повторить позже

Задача 6#134330Максимум баллов за задание: 7

Пусть $S$ — 100-элементное множество, состоящее из натуральных чисел, не превосходящих 10000. Отметим в пространстве все точки, каждая из координат которых принадлежит множеству $S.$ К каждой из 1000000 отмеченных точек $(x,y,z)$ прикрепим шарик с написанным на нём числом $x2+y2+z2 xy+yz+zx.$ На каком наибольшем количестве шариков может быть написано число, равное 2?

Источники: ВСОШ, РЭ, 2022, 11.5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Для начала нужно выяснить, при каких условиях точке может соответствовать число 2, какими соотношениями должны быть связаны x, y, z.

Подсказка 2:

Как насчёт того, чтобы рассмотреть уравнение x² + y² + z² = 2 • (xy + yz + zx) как квадратное относительно одной из переменных? Какие можно сделать выводы?

Подсказка 3:

Если его решить относительно x, получится √x = ±√y±√z. То есть подходят все такие тройки, для которых одно из чисел √x, √y, √z равно сумме двух других. Теперь можно делать оценку.

Подсказка 4:

Учтите, что в каждой такой тройке третий элемент восстанавливается по двум другим. Не забудьте про пример.

Показать ответ и решение

Назовём тройку натуральных чисел $(x,y,z),$ элементы которой принадлежат $S,$ хорошей, если

2 2 2 x + y + z =2(xy+ yz +zx). (∗)

Таким образом, нам надо найти наибольшее возможное количество хороших троек.

Выясним, когда тройка хорошая. Перепишем $(∗)$ как квадратное уравнение относительно $x$ :

2 2 x − 2x(y+ z)+ (y− z) = 0.

Решая его, получаем:

x= (y+ z)± 2√yz = (√y± √z)2,

откуда

√x-= ±√y± √z.

Иначе говоря, тройка является хорошей тогда и только тогда, когда одно из чисел $√x,$ $√y$ и $√z-$ равно сумме двух других.

Пусть $s1 < s2 < ...< s100$ — все элементы множества $S.$ Положим $ti = √si.$ Оценим количество хороших троек $(x,y,z),$ в которых $z$ — наибольшее число, то есть

tz = √z = √x +√y.

Заметим, что при любых $1≤ i< j ≤100$ есть не более одной такой тройки, в которой $√- x= ti$ и $√ - z = tj$ (по этим значениям восстанавливается $√- √ - √ - y = z− x$ ). Поэтому оцениваемое количество не превосходит числа таких пар $(i,j),$ то есть $C2100.$

Аналогично, количество хороших троек, в которых наибольшими являются $x$ и $y,$ не превосходит $C2100.$ Поэтому общее количество хороших троек не больше, чем $3⋅C2100.$

Эта оценка достигается, если положить $si =i2,$ то есть $ti = i:$ действительно, тогда при любых $i< j$ найдётся хорошая тройка $(si,sj − i2,sj).$

Ответ:

$3⋅C2 = 14850 100$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#135013Максимум баллов за задание: 7

Последовательность чисел $a ,a , 1 2$ …, $a 2022$ такова, что

3 3 an− ak ≥ n − k

для любых $n$ и $k$ таких, что $1 ≤n ≤2022$ и $1≤ k≤ 2022$ . При этом $a1011 =0.$ Какие значения может принимать $a2022$ ?

Источники: ВСОШ, РЭ, 2022, 9.6 и 11.6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Дано только лишь неравенство, но при этом требуется вычислить значение одного из членов. Единственный способ найти его при таком раскладе — зажать между каким-то числом. То есть доказать, что, с одной стороны, оно не больше некоторого числа x, а с другой стороны, не меньше этого же числа x. Отсюда будет следовать, что оно равно x.

Подсказка 2:

По всей видимости, вместо одного из индексов нужно подставить 2022. Но что подставить вместо второго, чтобы реализовать первую подсказку? В условии дано значение 1011-го члена. Почему бы не подставить 1011 вместо второго индекса?

Подсказка 3:

Учтите, подставить эти индексы можно двумя разными способами.

Показать ответ и решение

Записывая условие при $n =2022,$ $k= 1011$ и при $n =1011,$ $k= 2022,$ получаем

3 3 a2022 = a2022− a1011 ≥2022 − 1011

−a = a − a ≥ 10113− 20223, 2022 1011 2022

то есть $a2022 ≥ 20223 − 10113 ≥a2022.$ Отсюда и следует ответ.

Ответ:

3 3 3 a2022 =2022 − 1011 = 7⋅1011

Ошибка.
Попробуйте повторить позже

Задача 8#135023Максимум баллов за задание: 7

В вершины правильного 100-угольника поставили 100 фишек, на которых написаны номера 1, 2, …, 100, именно в таком порядке по часовой стрелке. За ход разрешается обменять местами некоторые две фишки, стоящие в соседних вершинах, если номера этих фишек отличаются не более чем на $k.$ При каком наименьшем $k$ серией таких ходов можно добиться расположения, в котором каждая фишка сдвинута на одну позицию по часовой стрелке (по отношению к своему начальному положению)?

Источники: ВСОШ, РЭ, 2022, 10.9 и 11.8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте придумать пример, он почти очевидный.

Подсказка 2:

Ясно, что такое можно реализовать для k = 50. Достаточно просто 99 раз сдвинуть фишку 50 против часовой стрелки.

Подсказка 3:

Чтобы доказать оценку на 50, попробуйте рассмотреть промежуток на окружности между фишками 1 и 100, который изначально без фишек.

Подсказка 4:

Попробуйте сравнить количество входов и заходов каждой из остальных фишек эту дугу. Также подумайте, через какую фишку 1 или 100 на дугу могут заходить другие фишки.

Показать ответ и решение

Пример. Фишку 50 последовательно 99 раз меняем со следующей против часовой стрелки. Получаем требуемое расположение.

Есть несколько способов доказать оценку, ниже мы приведём два из них.

Первый способ. Предположим, что при некотором $k <50$ требуемая расстановка получена.

В каждый момент времени считаем покрашенной дугу от фишки 100 до фишки 1 по часовой стрелке. Так как фишки 100 и 1 нельзя поменять за один ход, каждая конкретная фишка $m$ $(2≤ m ≤99)$ могла попасть на покрашенную дугу или покинуть покрашенную дугу лишь путём обмена с одной из фишек 1 или 100.

Поскольку изначально и в конце фишка $m$ не была на покрашенной дуге, она сделала одинаковое количество входов на покрашенную дугу и выходов с покрашенной дуги. При $m ≤50$ фишка $m$ не могла меняться с фишкой 100, поэтому она могла делать вход или выход только путём обмена с фишкой 1. При входе фишка 1 совершает сдвиг на 1 по часовой стрелке, а при выходе — на 1 против часовой стрелки. Проведём аналогичные рассуждения для фишек $m ≥ 51,$ которые не могут меняться с фишкой 1.

Тем самым, мы получаем, что фишки 1 и 100 совершают одинаковый сдвиг по и против часовой стрелки, поэтому они остаются на своих позициях. Противоречие.

_________________________________________________________________________________________________________________________________________________________________________________

Второй способ. Будем считать сдвиги фишек относительно их начальной позиции, причём сдвиг по часовой стрелке будет считаться с плюсом, против часовой — с минусом. Тогда при обмене двух фишек к сдвигу одной из них прибавляется +1, а другой — $− 1.$ Значит, в результате проведённых операций общая сумма сдвигов будет равна 0.

Рассуждаем от противного: пусть при $k <50$ каждая фишка $i$ в итоге сдвинута на одну позицию по часовой стрелке, т.е. её сдвиг оказался равным $1+100ti$ (здесь $ti$ — целое «число оборотов» по часовой стрелке, в частности при $ti <0$ фишка $i$ сделала $|ti|$ оборотов против часовой стрелки). Тогда суммарный сдвиг всех 100 фишек равен

100(t1+ t2+...+t100)+ 100.

Поскольку он должен равняться 0, имеем

t1+ t2 +...+ t100 = −1.

Поскольку $k< 50,$ фишки с номерами $i$ и $j,$ где $j ≥i+ 50,$ не могли меняться местами, поэтому их сдвиги в любой момент заведомо отличаются меньше чем на 100, значит количества оборотов $ti$ и $tj$ равны при $j ≥i+ 50.$ Отсюда имеем $t1 =t51,$ $t2 = t52,$ …, $t50 =t100,$ Тогда сумма

t1+ t2+ ...+ t100 = 2(t1+ t2+ ...+ t50)

— чётна, а значит не равна $− 1.$ Противоречие.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 9#135024Максимум баллов за задание: 7

Произведение цифр натурального числа $n$ равно $x,$ а произведение цифр числа $n +1$ равно $y.$ Может ли так случиться, что произведение цифр некоторого натурального числа $m$ равно $y− 1,$ а произведение цифр числа $m +1$ равно $x− 1?$

Источники: ВСОШ, РЭ, 2022, 11.7 (см. olympiads.mccme.ru)

Показать ответ и решение

Из условия следует, что $x,y ≥1,$ поскольку произведение цифр натурального числа не может быть отрицательным. Следовательно, числа $n$ и $n +1$ не содержат нулей в десятичной записи. Тогда эти числа отличаются лишь последней цифрой, причём у числа $n +1$ она больше на один. Таким образом, $y > x.$ Если $x − 1> 0,$ то, рассуждая аналогично, мы получим, что $y− 1 <x − 1,$ это противоречит доказанному выше. Следовательно, $x − 1= 0.$ Тогда $x= 1,$ и в десятичной записи числа $n$ все цифры равны 1. Отсюда следует, что в числе $n+ 2$ последняя цифра — двойка, а остальные цифры — единицы, поэтому $y =2.$ Значит, $y − 1 =1,$ и число $m$ состоит лишь из единиц. Но тогда число $m +1$ не содержит нулей в десятичной записи. Однако, произведение его цифр равно нулю, противоречие.

Ответ:

не может

Ошибка.
Попробуйте повторить позже

Задача 10#135026Максимум баллов за задание: 7

Трапеция $ABCD$ с основаниями $AD$ и $BC$ вписана в окружность $ω.$ Диагонали $AC$ и $BD$ пересекаются в точке $P.$ Точка $M$ — середина отрезка $AB.$ Серединный перпендикуляр к отрезку $AD$ пересекает окружность $ω$ в точках $K$ и $L.$ Точка $N$ — середина дуги $CD$ описанной окружности треугольника $PCD,$ не содержащей точку $P$ . Докажите, что точки $K,L,M$ и $N$ лежат на одной окружности.

Показать доказательство

Обозначим через $O$ центр окружности, описанной около трапеции $ABCD.$ Тогда

∠COD =2∠CAD =∠P AD +∠ADP =∠CP D.

Здесь мы воспользовались тем, что центральный угол вдвое больше вписанного, и что внешний угол треугольника равен сумме двух внутренних, с ним не смежных.

Следовательно, точка $O$ лежит на окружности $γ,$ описанной около треугольника $CP D,$ и поскольку $OC = OD,$ то $O$ — середина дуги $CP D.$ Тогда отрезок $ON$ — диаметр окружности $γ,$ а прямая $ON$ — серединный перпендикуляр к отрезку $CD.$ В частности, середина отрезка $CD,$ обозначим её через $S,$ лежит на отрезке $ON.$ Из сказанного выше,

∘ ∠OCN = 90 = ∠CSN.

Значит, окружность, описанная около треугольника $SCN,$ касается прямой $OC,$ поэтому

OS ⋅ON = OC2 = OK ⋅OL.

Отметим точку $S′,$ симметричную точке $S$ относительно точки $O.$ Тогда

OK ⋅OL= OS′⋅ON,

поэтому точки $′ S,K,L,N$ лежат на одной окружности.

$PIC$

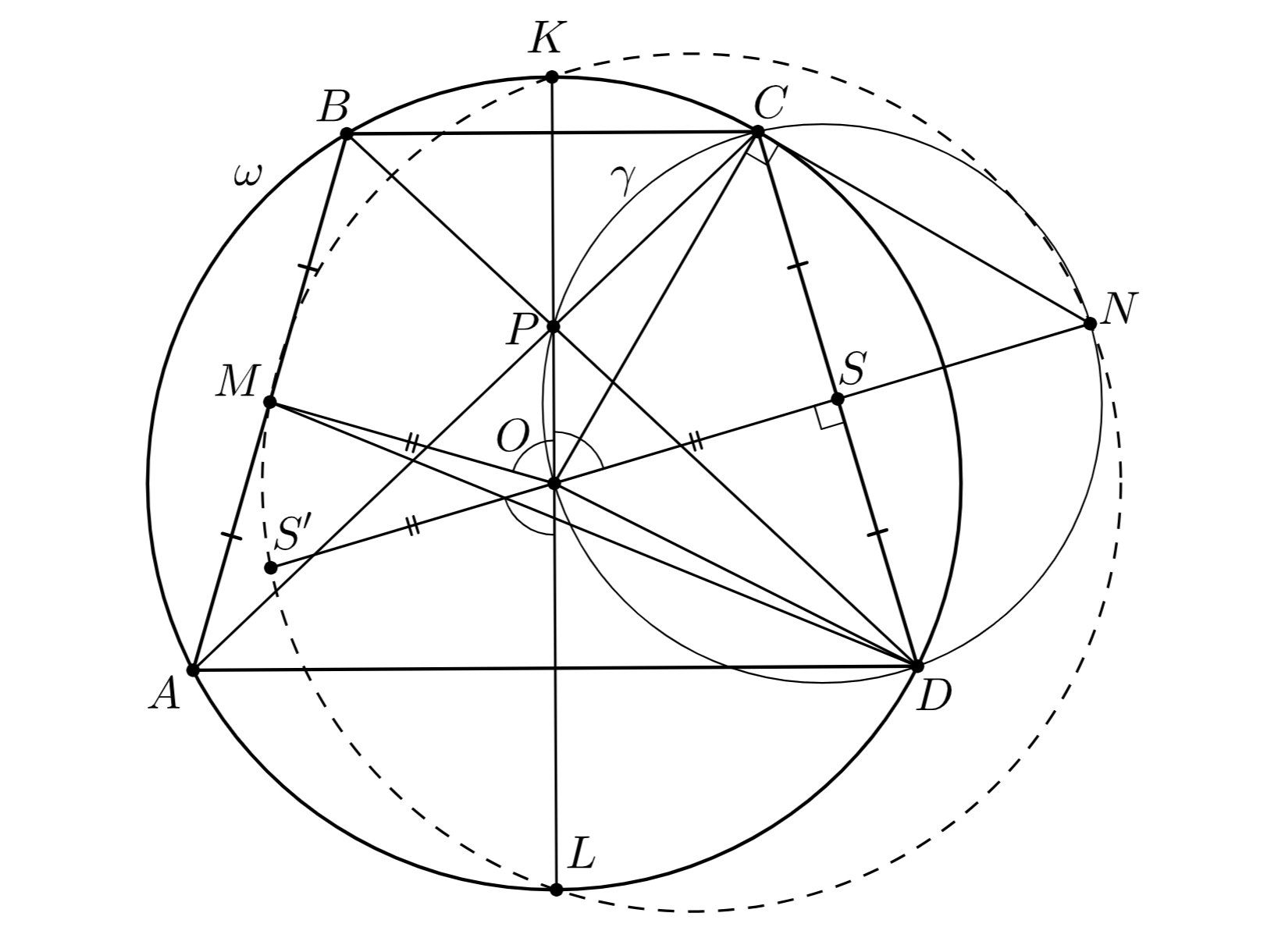
Теперь заметим, что точки $M$ и $S$ симметричны относительно прямой $KL.$ Значит,

OS′ = OS = OM и ∠LOS′ = ∠KOS = ∠KOM.

Таким образом, точки $M$ и $S′$ симметричны относительно серединного перпендикуляра к $KL.$ Следовательно, точки $K,$ $M,$ $S′$ и $L$ лежат на одной окружности. Из сказанного выше, на этой окружности лежит также и точка $N,$ что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 11#135027Максимум баллов за задание: 7

Даны неотрицательные числа $a,b,c,d$ такие, что $a+b+ c+ d= 8.$ Докажите, что

---a3--- ---b3-- ---c3---- ---d3--- a2+ b+c +b2+ c+ d + c2+d +a +d2+ a+ b ≥ 4.

Источники: ВСОШ, РЭ, 2022, 11.10 (см. olympiads.mccme.ru)

Показать доказательство

Первое решение. Заметим, что

a3 a(b+ c) a(b+ c) √b-+c- a2-+b+-c = a− a2+-b+c-≥a −2a√b+-c = a−-2--.

Здесь мы оценили знаменатель по неравенству о средних:

a2 +b+ c≥ 2a√b-+c.

Сложим полученное неравенство с тремя аналогичными. Теперь нам достаточно доказать, что

√---- √ ---- √ ---- √---- a+ b+c+ d− -a+-b− --b+c −--c+d − -d+-a≥ 4. 2 2 2 2

Поскольку

a+ b+ c+d =8,

это равносильно неравенству

√ ---- √---- √---- √ ---- --a+-b+ -b+-c+ -c+-d+ --d+a-≤ 4. 2 2 2 2

Но из неравенства между средним арифметическим и средним квадратичным мы получаем, что

√a-+-b √c+-d ∘ (√a+-b)2-+(√c+-d)2- --2-- + --2--≤ ⋅-------2------- =2,

и, аналогично,

√---- √---- -b+-c+ -d+-a-≤2. 2 2

Складывая эти два неравенства, получаем требуемое.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. По неравенству Коши-Буняковского-Шварца в форме Энгеля

---a3---- ---b3-- ---c3---- ---d3--- a2+ b+c + b2+ c+d + c2 +d+ a + d2+ a+ b ≥

2 2 2 22 ≥ --2----------2(a-+b-+-c-+2d-)-------2------. a(a + b+ c)+ b(b + c+d)+ c(c + d+ a)+ d(d + a+ b)

Таким образом, достаточно доказать, что

(a2+ b2+c2+ d2)2 ≥ 4(a3+ b3+c3+ d3+ ab+ bc+cd+ da+ 2ac+ 2bd).

Заметим, что

32= (a-+b+-c+-d)2-=ab+ bc +cd+ da+ac+ bd+ a2-+c2+ b2+-d2-≥ 2 2 2

≥ ab+bc+ cd+da+ 2ac+2bd

поэтому достаточно проверить, что

2 2 2 2 2 3 3 3 3 (a + b+ c + d) ≥ 4(a + b +c + d +32). (∗)

Сделаем замену

a= 2+ x, b =2+ y, c= 2+ z, d =2 +t.

Тогда

x +y+ z+ t=a +b+ c+ d− 8 =0,

a2 +b2+ c2 +d2 = 4⋅22+2 ⋅2(x+ y+ z+t)+ x2+y2+ z2+ t2 = 16+ x2+y2+ z2+ t2,

a3+ b3 +c3+ d3 =4 ⋅23+ 3⋅22(x+ y+ z+ t)+ 3⋅2(x2+ y2+ z2 +t2)+x3+ y3+z3+ t3.

Неравенство $(∗)$ примет вид

((x2+ y2+ z2 +t2)+16)2 ≥4 (x3+ y3+ z3 +t3+ 6(x2+ y2+z2+ t2)+ 64).

После раскрытия и сокращения остаётся доказать, что

(x2+ y2+ z2 +t2)2+ 8(x2 +y2+ z2+t2)≥4(x3+ y3 +z3+ t3).

Остаётся заметить, что

(x2+ y2+ z2+t2)2+ 8(x2 +y2+ z2+t2)≥ x4 +y4+ z4+t4+ 4x2 +4y2+ 4z2+ 4t2 ≥4(x3+ y3 +z3+ t3).

Первое неравенство получается раскрытием скобок: после сокращения в левой его части остаются лишь неотрицательные слагаемые. Второе получается сложением четырёх неравенств о средних вида $4 2 3 x + 4x ≥ 4x.$