ДВИ 2025
Ошибка.
Попробуйте повторить позже
Радиус сферы, вписанной в правильную треугольную пирамиду, равен 1. Радиус окружности, вписанной в основание этой пирамиды, равен
Найдите радиус сферы, описанной около этой пирамиды.
Источники:
Подсказка 1
Давайте сначала разберемся с тем, где находится центр вписанной сферы.
Подсказка 2
Так как пирамида — правильная, центр вписанной сферы будет лежать на высоте. Как нам теперь этим воспользоваться?
Подсказка 3
Попробуйте перейти в некоторую «удобную» плоскость. Нам надо как-то воспользоваться радиусом окружности, вписанной в основание.
Подсказка 4
Пусть M — середина BC. Рассмотрите плоскость ASM.
Подсказка 5
Это равнобедренный треугольник. Посмотрите на окружность, полученную сечением вписанной сферы плоскостью ASM.
Подсказка 6
Попробуйте связать ∠AMS и радиус окружности, вписанной в основание.
Подсказка 7
В этом Вам может помочь радиус вписанной сферы.
Подсказка 8
r ₁ = r₂ ⋅ tg(∠AMS/2), где r ₁ — радиус вписанной сферы, r₂ — радиус окружности, вписанной в основание пирамиды. Подставьте известные значения.
Подсказка 9
Теперь надо понять, как вычислить высоту при помощи этих данных.
Подсказка 10
H = r₂ ⋅ tg(∠AMS).
Подсказка 11
Осталось только найти радиус сферы, описанной около пирамиды. Где будет лежать ее центр?
Подсказка 12
Также на высоте пирамиды! Какая есть формула для нахождения радиуса описанной сферы?
Подсказка 13
Он равен (H² + R²)/2H, где H — высота пирамиды, R — радиус окружности, описанной около основания. Собственно, его и хотим найти.
Подсказка 14
Заметим, что основание пирамиды является правильным треугольником. Тогда как связаны радиусы вписанной и описанной окружностей?
Подсказка 15
Радиус описанной окружности вдвое больше!
1. Нахождение высоты пирамиды
Пусть дана правильная треугольная пирамида с вершиной
и центром основания
Центр вписанной сферы
лежит на её
высоте
Пусть
— середина ребра основания
Тогда
— апофема пирамиды. Рассмотрим осевое сечение
которое является равнобедренным треугольником. В этом сечении круг, являющийся сечением вписанной сферы,
вписан в угол
Этот угол образован апофемой пирамиды
и радиусом вписанной в основание окружности
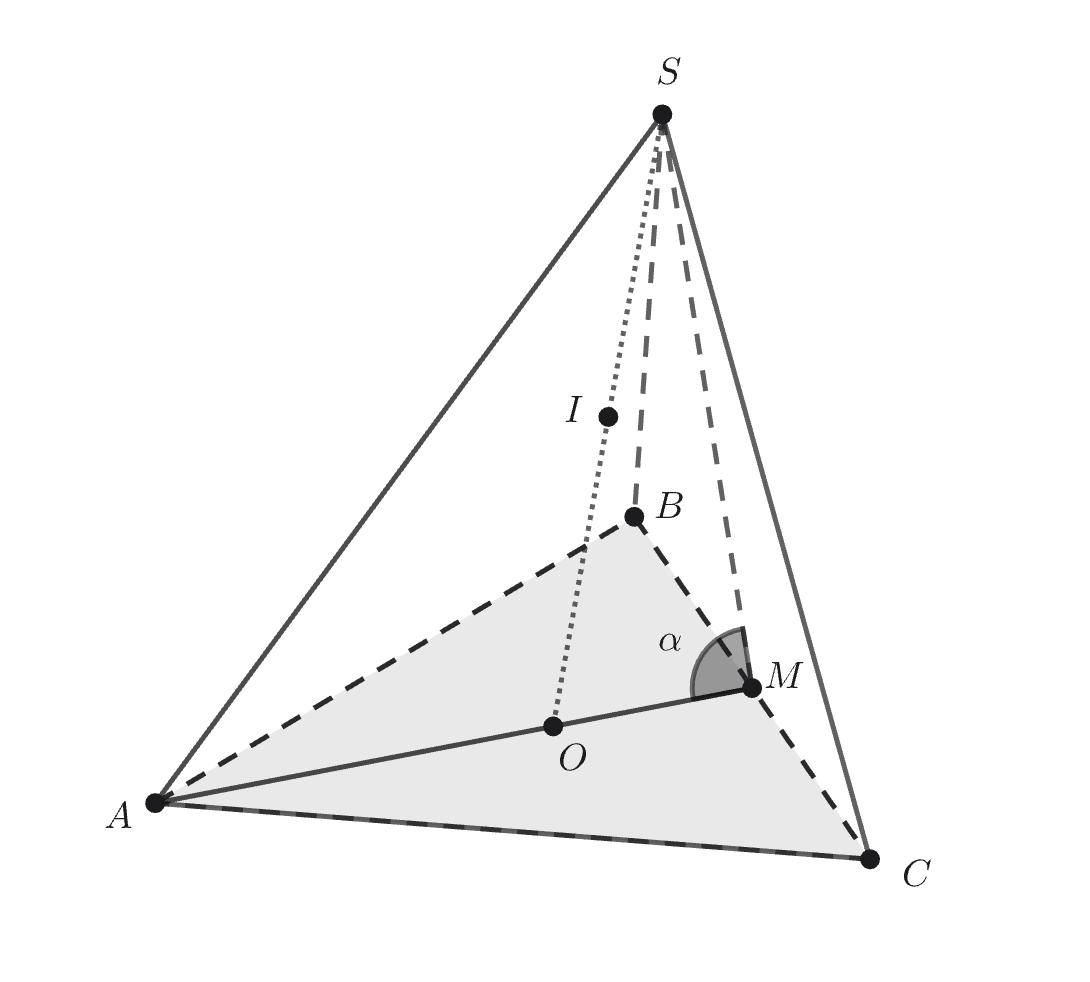
Пусть — радиус вписанной сферы,
— радиус окружности, вписанной в основание пирамиды, и
— двугранный
угол при ребре основания. Они связаны соотношением
Подставим известные значения:
Отсюда находим :
Теперь найдем по формуле двойного угла:
Вычислим :
Подставим в формулу для :
Высота пирамиды связана с
и углом
через тот же треугольник в сечении:
2. Нахождение радиуса описанной сферы
Центр описанной сферы также лежит на высоте пирамиды. Радиус описанной сферы для правильной пирамиды можно найти по
формуле
где — радиус окружности, описанной около основания.
Основание пирамиды — правильный треугольник. Для правильного треугольника радиус описанной окружности вдвое больше
радиуса вписанной окружности
:
Мы получили, что Это означает, что центр описанной сферы совпадает с центром основания пирамиды. В этом
случае радиус описанной сферы равен радиусу окружности, описанной около основания.
Проверим это, подставив в общую формулу для
:
Итак,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




