ДВИ 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Найдите наибольшее целое число, меньшее числа
Источники:
Подсказка 1
Как Вы думаете, какими числами удобно ограничить сумму √7 + √8? Может, надо как-то её увеличить и уменьшить?
Подсказка 2
А если взять суммы √7 + √7 и √8 + √8?
Подсказка 3
Оцените числа 2√7 и 2√8. Для удобства можно занести двойки под корни.
Заметим, что
Оценим число снизу:
Оценим число сверху:
Получаем цепочку неравенств:
Отсюда видим, что наибольшее целое число, меньшее числа — это 5.
Ошибка.
Попробуйте повторить позже
Дана последовательность действительных чисел, удовлетворяющих при каждом натуральном
равенству
Найдите если известно, что
и
Источники:
Подсказка 1
Давайте просто вычислим несколько первых членов последовательности, может быть, нам удастся увидеть закономерность?
Подсказка 2
Есть подозрение, что нечетные члены последовательности, начиная с третьего, всегда равны предыдущему члену, а следующий четный член в 4 раза больше предыдущего нечетного! Убедитесь в правдивости этой гипотезы и определите, чему равен 2025 член последовательности.
Найдём несколько первых членов последовательности:
Предположим, что — некоторое четное натуральное число и
вычислим
и
Таким образом, наша последовательность имеет вид:
Тогда 2025-ый член последовательности равен соответственно,
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Подсказка 1
Какие преобразования полезно делать в логарифмических неравенствах?
Подсказка 2
Воспользуйтесь свойствами таким образом, чтобы у всех логарифмов основание стало равно 2, а аргумент – х.
Подсказка 3
После преобразований становится очевидна правильная замена! Теперь у нас есть довольно простое неравенство, которое сразу хочется возвести в квадрат. Но будьте осторожны – не забывайте, что неравенство можно возводить в квадрат, только если Вы уверены, что обе его части неотрицательны!
Подсказка 4
С левой частью все понятно – она всегда неотрицательна на ОДЗ, а вот с правой частью нужно рассмотреть два разных случая. После рассмотрения двух случаев объедините полученные решения, вернитесь к исходной переменной и не забудьте учесть ОДЗ!
Запишем ОДЗ:
На ОДЗ верны преобразования:
Сделаем замену тогда неравенство примет вид:
Если то неравенство выполнено на ОДЗ, то есть все
нам подходят. Если же
возведем неравенство в квадрат
и получим:
Учитывая, что мы рассматриваем случай, когда получаем:
Объединяем со случаем
Заметим, что неравенство верно при любом действительном
так что первое условие из ОДЗ выполнено
автоматически. Вернёмся к исходной переменной:
С учётом ОДЗ получаем ответ:
Ошибка.
Попробуйте повторить позже
Решите уравнение
Источники:
Подсказка 1
Сразу избавляется от двойных углов и от знаменателя (однако помним, что у нас есть ограничение – знаменатель не должен быть равен нулю). Как стоит преобразовать данное уравнение для удобства?
Подсказка 2
Сделайте так, чтобы в уравнении остался только один вид тригонометрической функции.
Подсказка 3
Воспользуйтесь ОТТ, чтобы получить квадратное уравнение относительно косинуса! Теперь просто решаем его и делаем обратную замену.
Воспользуемся формулой синуса двойного угла:
Перенесем все в одну сторону и умножим уравнение на
Сделаем замену
Так как не может быть больше 1, то
Заметим, что данная серия не зануляет знаменателей в исходном уравнении, так что эта серия и является ответом.
Ошибка.
Попробуйте повторить позже
На сторонах треугольника
отмечены точки
соответственно. На
и на
как на диаметрах построены
окружности. Эти окружности касаются отрезка
в одной и той же точке. Найдите
если известно, что
и что
Источники:
Подсказка 1
Так, мы видим две окружности и общую к ним касательную. Какую теорему можно записать в этом случае?
Подсказка 2
Воспользуйтесь теоремой о касательной и секущей (степень точки K относительно окружностей).
Подсказка 3
Мы знаем длину стороны BC, а найти нужно сторону DF. Можно ли сделать какой-то вывод про △ADF и △ACB?
Подсказка 4
Докажите подобие треугольников и найдите коэффициент подобия.
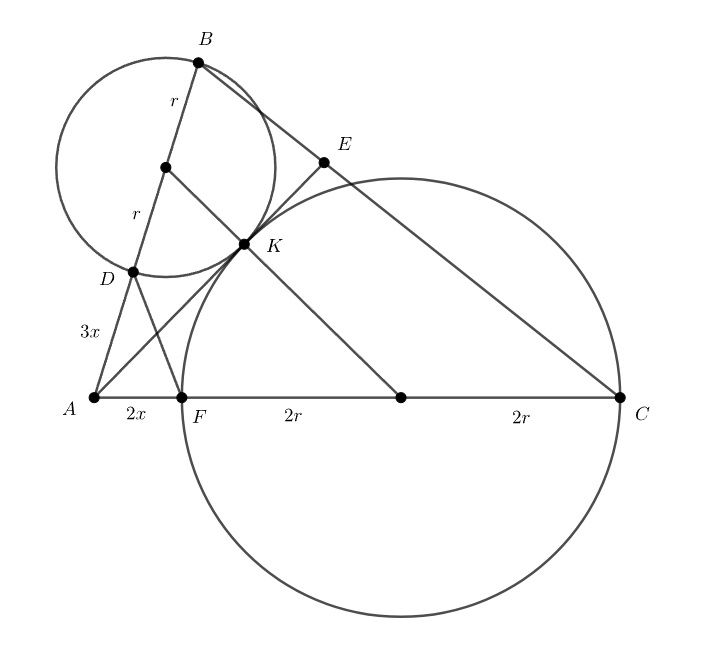
Так как и
— диаметры и
обозначим радиус окружности, построенной на
за
а на
—
Пусть
окружности касаются
в точке
Тогда
— касательная. По теореме о касательной и секущей
Приравнивая выражения, получим:
Получаем, что треугольники и
подобны.
Положим тогда
Тогда получим:
Теперь найдем коэффициент подобия
Тогда
Ошибка.
Попробуйте повторить позже
Положительные действительные числа удовлетворяют неравенствам
при всех натуральных таких что
Найдите наименьшее возможное значение выражения
Источники:
Подсказка 1
Можно сразу поделить последнюю дробь числителя на a₇, но что делать потом?
Подсказка 2
Попробуем оценить числитель. Приведите его дроби к одному знаменателю.
Подсказка 3
Как воспользоваться условием для aᵢ + aⱼ?
Подсказка 4
Оценим все aᵢ через a₇. Например, a₁ + a₆ ≥ a₇.
Подсказка 5
Вам также может помочь расширение оценки из условия для трех слагаемых. Выведите его, применив 2 раза исходное.
Подсказка 6
Чтобы подобрать пример, надо думать проще. Сколько у нас слагаемых в числителе?
Подсказка 7
Семь. А если знаменатель будет равен семи?
Так как то верно
Приведём первые шесть слагаемых числителя искомого выражения к общему знаменателю и оценим:
Воспользуемся оценками:
Суммируя, получаем
Тогда для всей суммы получаем:
Значит,
Такой случай реализуется, например, при для
Условие задачи выполняется
Тогда искомое выражение
принимает значение
Ошибка.
Попробуйте повторить позже
Радиус сферы, вписанной в правильную треугольную пирамиду, равен 1. Радиус окружности, вписанной в основание этой пирамиды, равен
Найдите радиус сферы, описанной около этой пирамиды.
Источники:
Подсказка 1
Давайте сначала разберемся с тем, где находится центр вписанной сферы.
Подсказка 2
Так как пирамида — правильная, центр вписанной сферы будет лежать на высоте. Как нам теперь этим воспользоваться?
Подсказка 3
Попробуйте перейти в некоторую «удобную» плоскость. Нам надо как-то воспользоваться радиусом окружности, вписанной в основание.
Подсказка 4
Пусть M — середина BC. Рассмотрите плоскость ASM.
Подсказка 5
Это равнобедренный треугольник. Посмотрите на окружность, полученную сечением вписанной сферы плоскостью ASM.
Подсказка 6
Попробуйте связать ∠AMS и радиус окружности, вписанной в основание.
Подсказка 7
В этом Вам может помочь радиус вписанной сферы.
Подсказка 8
r ₁ = r₂ ⋅ tg(∠AMS/2), где r ₁ — радиус вписанной сферы, r₂ — радиус окружности, вписанной в основание пирамиды. Подставьте известные значения.
Подсказка 9
Теперь надо понять, как вычислить высоту при помощи этих данных.
Подсказка 10
H = r₂ ⋅ tg(∠AMS).
Подсказка 11
Осталось только найти радиус сферы, описанной около пирамиды. Где будет лежать ее центр?
Подсказка 12
Также на высоте пирамиды! Какая есть формула для нахождения радиуса описанной сферы?
Подсказка 13
Он равен (H² + R²)/2H, где H — высота пирамиды, R — радиус окружности, описанной около основания. Собственно, его и хотим найти.
Подсказка 14
Заметим, что основание пирамиды является правильным треугольником. Тогда как связаны радиусы вписанной и описанной окружностей?
Подсказка 15
Радиус описанной окружности вдвое больше!
1. Нахождение высоты пирамиды
Пусть дана правильная треугольная пирамида с вершиной
и центром основания
Центр вписанной сферы
лежит на её
высоте
Пусть
— середина ребра основания
Тогда
— апофема пирамиды. Рассмотрим осевое сечение
которое является равнобедренным треугольником. В этом сечении круг, являющийся сечением вписанной сферы,
вписан в угол
Этот угол образован апофемой пирамиды
и радиусом вписанной в основание окружности
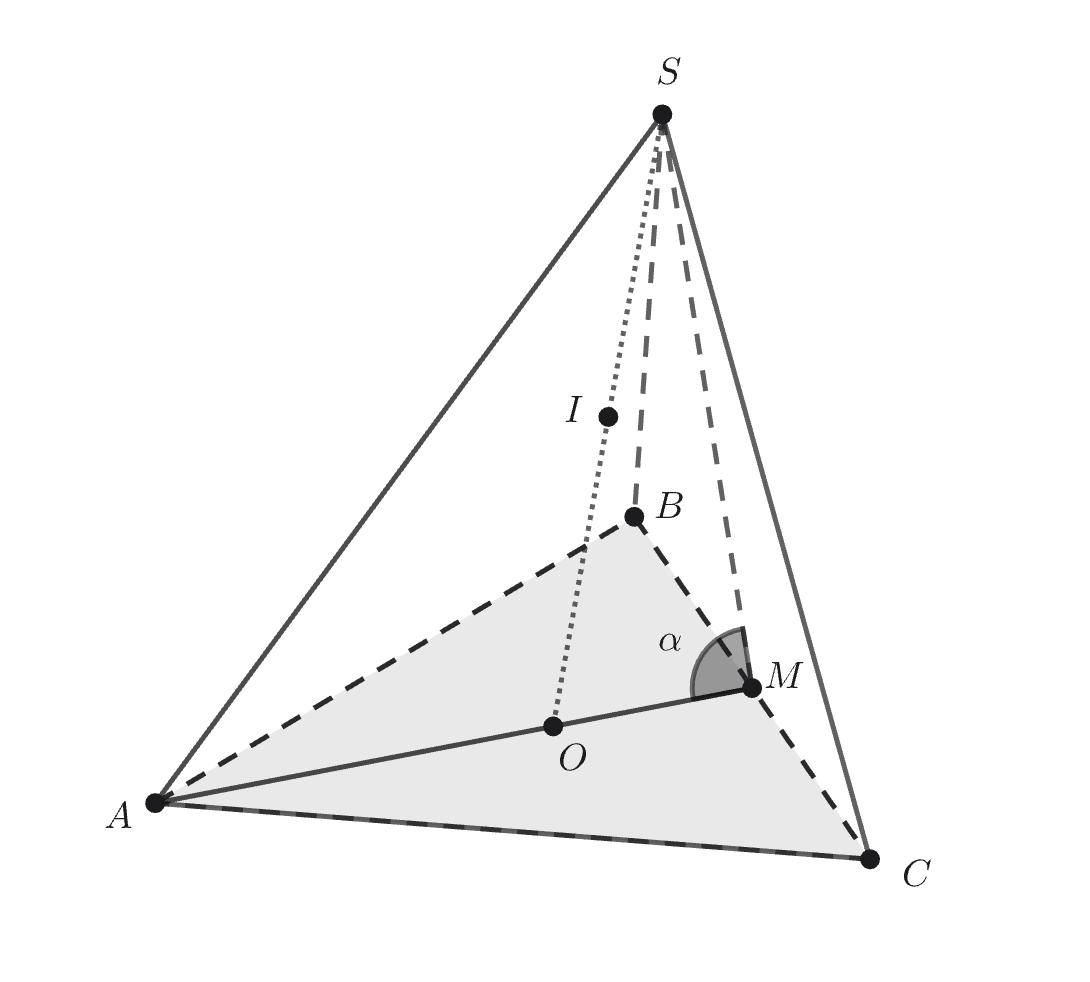
Пусть — радиус вписанной сферы,
— радиус окружности, вписанной в основание пирамиды, и
— двугранный
угол при ребре основания. Они связаны соотношением
Подставим известные значения:
Отсюда находим :
Теперь найдем по формуле двойного угла:
Вычислим :
Подставим в формулу для :
Высота пирамиды связана с
и углом
через тот же треугольник в сечении:
2. Нахождение радиуса описанной сферы
Центр описанной сферы также лежит на высоте пирамиды. Радиус описанной сферы для правильной пирамиды можно найти по
формуле
где — радиус окружности, описанной около основания.
Основание пирамиды — правильный треугольник. Для правильного треугольника радиус описанной окружности вдвое больше
радиуса вписанной окружности
:
Мы получили, что Это означает, что центр описанной сферы совпадает с центром основания пирамиды. В этом
случае радиус описанной сферы равен радиусу окружности, описанной около основания.
Проверим это, подставив в общую формулу для
:
Итак,
Ошибка.
Попробуйте повторить позже
Известно, что Найдите наименьшее целое число, превосходящее
Источники:
Подсказка
Давайте попробуем вычислить значение функции в интересующей нас точке. Какое наименьшее целое число будет больше полученного значения?
Подставим
Таким образом, наименьшее целое число, превосходящее — это число
Ошибка.
Попробуйте повторить позже
Дана последовательность действительных чисел, удовлетворяющих при каждом натуральном
равенству
Последовательность определяется соотношениями
и
Найдите
Источники:
Подсказка 1
Давайте поработаем с последовательностью а, можем ли мы выразить aₙ через аₙ₋₁, не используя в записи другие члены последовательности?
Подсказка 2
aₙ = 2аₙ₋₁, то есть каждый последующий член нашей последовательности в два раза больше предыдущего! А как называется такая последовательность? Определите а₁, чтобы записать формулу для n-ого члена последовательности.
Подсказка 3
Имеем геометрическую прогрессию с первым членом, равным единице, и знаменателем, равным двойке! Теперь давайте поработаем со второй последовательностью: можем ли мы выразить bₙ₊₁, не используя других членов наших последовательностей?
Подсказка 4
Воспользовавшись формулой суммы первых n членов геометрической прогрессии, найдём формулу для bₙ₊₁, а дальше остается просто посчитать искомую сумму!
Рассмотрим последовательность
Тогда для любого
Подставим второе равенство в первое:
Пользуясь ранее найденным получаем
Теперь рассмотрим вторую последовательность:
По формуле суммы геометрической прогрессии:
Таким образом,
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Подсказка 1
Так как основание логарифмов не зависит от х, мы спокойно можем от него избавиться и перейти к рассмотрению равносильного неравенства. Только не забудьте учесть, что 0.5 < 1, и записать ОДЗ!
Подсказка 2
Действуем по классике: переносим все в одну сторону, приводим к общему знаменателю и раскладываем на множители, а дальше так и напрашивается метод рационализации! Кроме того, обратите внимание на заведомо положительные множители. Для удобства от них можно избавиться.
Выпишем ОДЗ:
Перейдём от исходного неравенства к равносильному:
Пользясь тем, что при любых
а также методом рационализации, получаем:
Решением этого неравенства является
Ошибка.
Попробуйте повторить позже
Решите уравнение
Источники:
Подсказка 1
С тангенсами и котангенсами не очень приятно работать, так что давайте перейдем к более простым функциям! И, конечно, не забудем записать ОДЗ.
Подсказка 2
Обычно мы переносим все в одну сторону, приводим к общему знаменателю и пытаемся увидеть там что-то хорошее – давайте и тут поступим так же, правда, в этот раз искать нужно вовсе не разложение на множители...
Подсказка 3
Если внимательно посмотреть на полученный числитель, то какая-то его часть свернется в квадрат суммы, а для суммы можно будет использовать ОТТ! После такого преобразования уравнение становится совсем простым, из него можно найти sin(2x), а отсюда уже и искомую переменную.
Наличие в выражении тангенса и котангенса обязывает нас иметь в виду ограничения:
Перепишем тангенс и котангенс по определению и приведём выражение к общему знаменателю:
Таким образом:
Ошибка.
Попробуйте повторить позже
Окружности и
находятся внутри окружности
касаются окружности
в точках
и
соответственно и касаются друг
друга внешним образом в точке
Пусть
— центр окружности
и пусть
— точка пересечения прямой
с отрезком
Найдите отношение
если известно, что радиус окружности
в три раза больше радиуса окружности
и в пять раз больше
радиуса окружности
Источники:
Пусть и
— центры окружностей
и
соответственно. Обозначим
По
условию
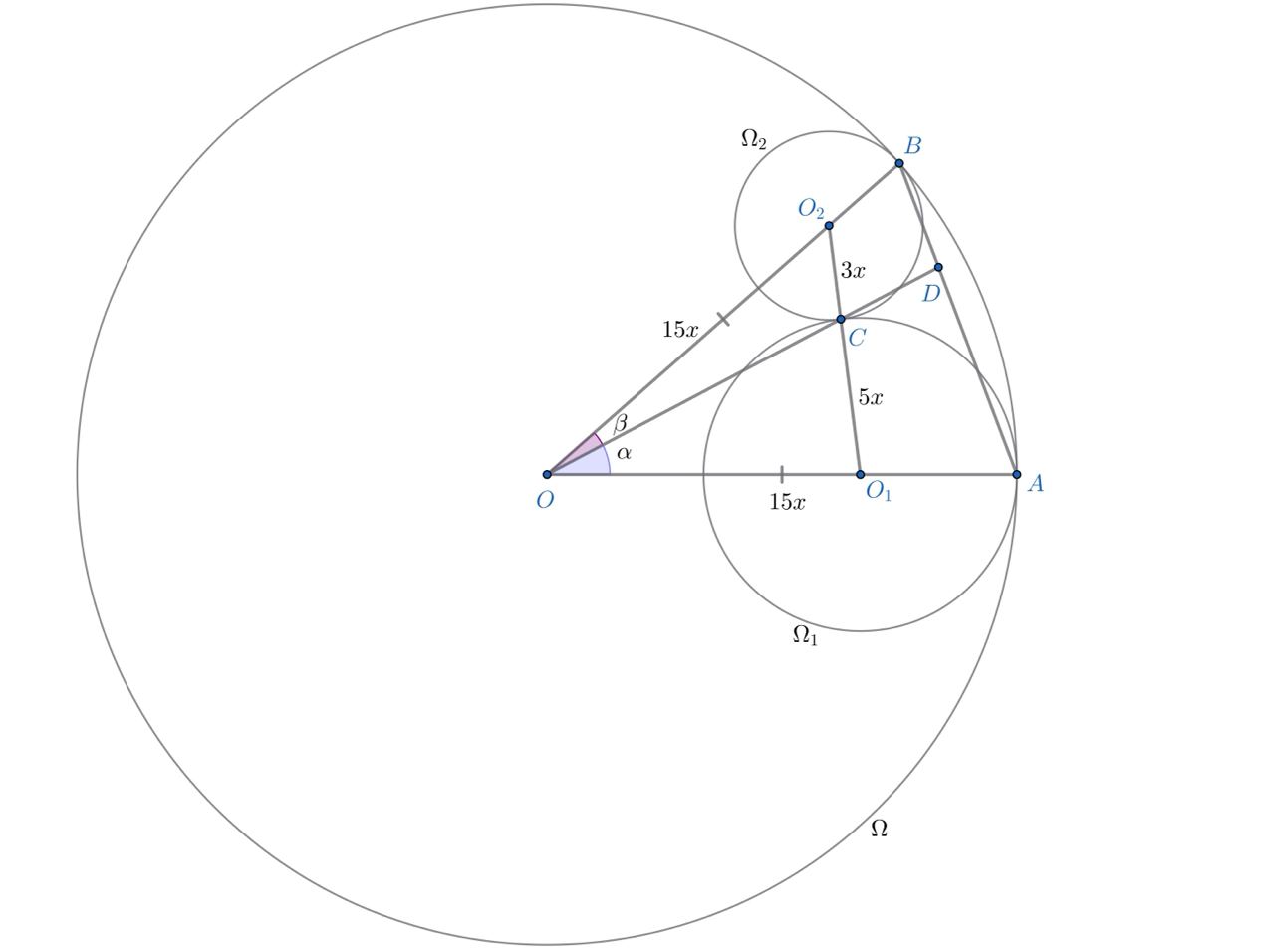
Заметим, что
Теперь найдем искомое отношение из равенства:
Ошибка.
Попробуйте повторить позже
Последовательность действительных чисел удовлетворяет неравенствам
при каждом и неравенству
Найдите все возможные значения
Источники:
Для упрощения неравенств введем новую последовательность Пусть
Из того, что подкоренное выражение должно быть неотрицательным: то есть
для всех
Перепишем данные неравенства в терминах последовательности
Первое неравенство:
Первое неравенство принимает вид:
Второе неравенство:
Второе неравенство принимает вид:
Теперь у нас есть система из 2025 неравенств для неотрицательных чисел :
Просуммируем все эти неравенства:
Перенесем все члены в одну сторону:
Сумма квадратов действительных чисел всегда неотрицательна, поэтому единственный случай, когда полученное неравенство выполняется — это когда сумма равна нулю:
Сумма неотрицательных слагаемых равна нулю тогда и только тогда, когда каждое слагаемое равно нулю. Следовательно, для
всех
Мы нашли, что единственно возможное значение для каждого члена последовательности равно 1. Нас просят найти значение
Вернемся к исходной замене:
Таким образом, единственное возможное значение для — это 2025.
Ошибка.
Попробуйте повторить позже
Все три плоских угла при вершине тетраэдра
равны
Найдите
если известно, что
и
Источники:
Обозначим Выразим
через теорему косинусов для треугольников
и
и приравняем
результаты:
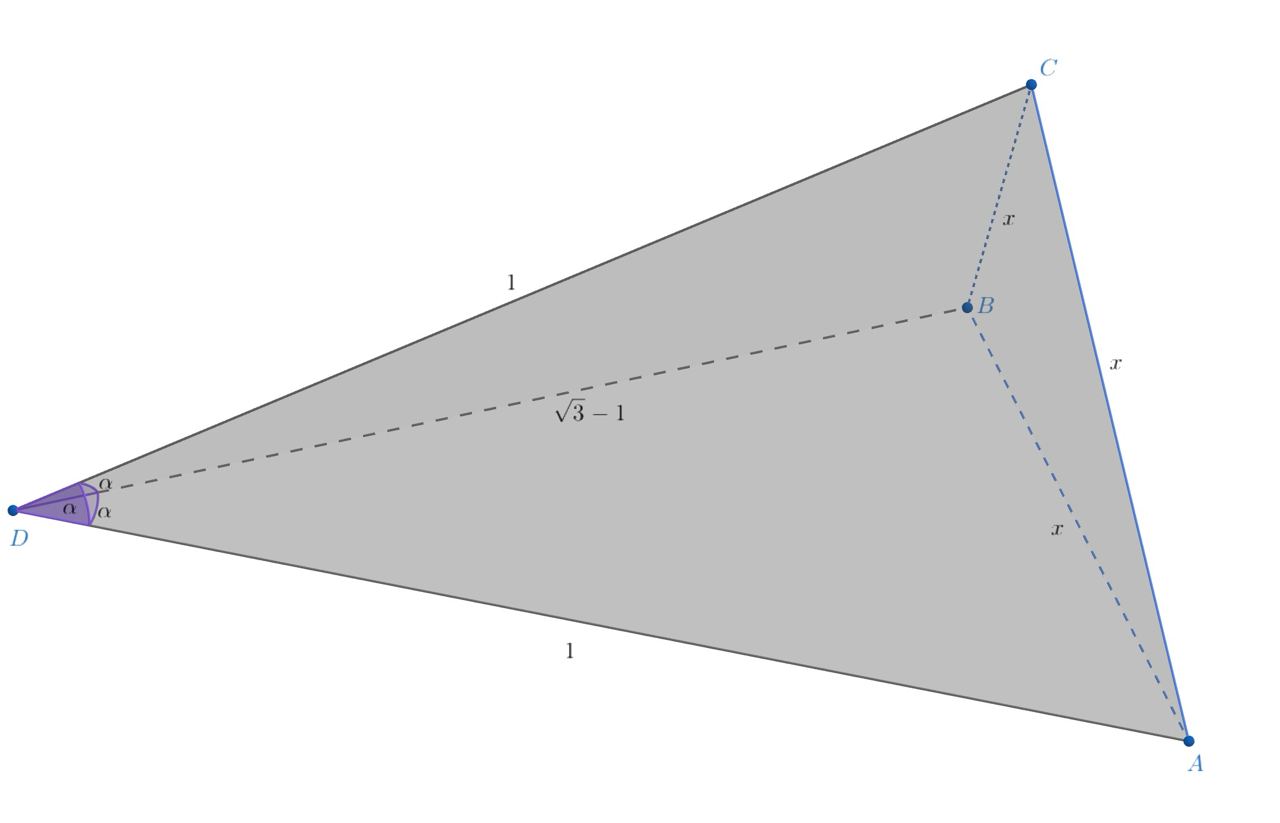
Если тогда треугольник
равнобедренный с углами
при основании. По теореме синусов
для треугольника
Отсюда получаем:
Запишем теорему косинусов для треугольника
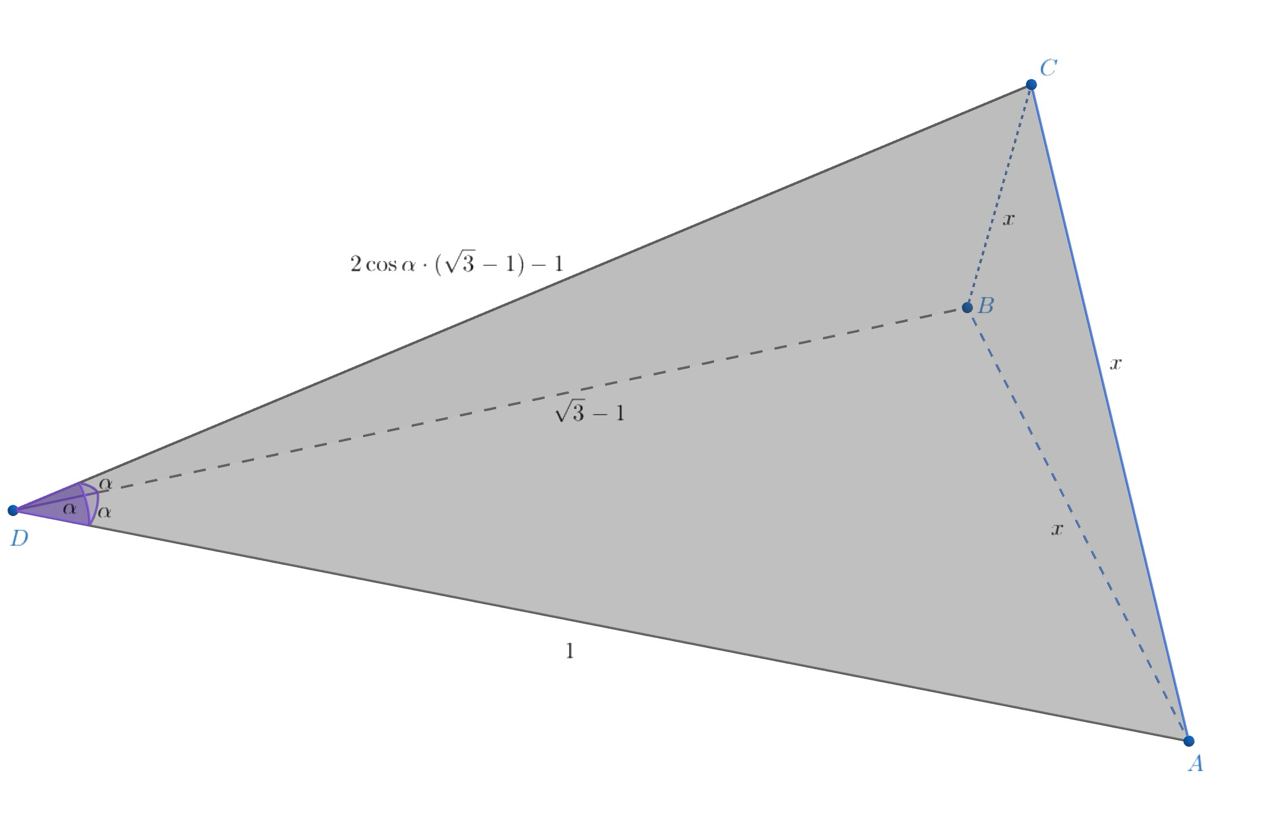
Если то
Выразим через теорему косинусов для треугольников
и
приравняем результаты:
Так как
этот корень убираем из рассмотрения.
Если
то
Сравним полученный косинус с единицей:
Так как
Это невозможно, следовательно, единственным ответом к задаче является
Ошибка.
Попробуйте повторить позже
Найдите в явном виде целое число, задающееся выражением
Источники:
Подсказка 1
Какой стандартный приём помогает сложить две произвольные дроби?
Подсказка 2
Надо просто привести дроби к общему знаменателю и посчитать. А как возвести дробь в -1 степень?
Подсказка 3
Правильно, чтобы возвести дробь в -1 степень, её нужно перевернуть.
Последовательно приведём дроби к общему знаменателю
Ошибка.
Попробуйте повторить позже
Строго возрастающая последовательность натуральных чисел удовлетворяет при каждом натуральном
соотношению
Найдите все возможные значения если известно, что
Источники:
Подсказка 1
Как воспользоваться условием о том, что a₁ = 1?
Подсказка 2
Можно ли с его помощью вычислить несколько первых членов последовательности?
Подсказка 3
Заметим, что так как последовательность строго возрастающая, 1 = a₁ < a₂ < a₃. Попробуйте выразить a₃.
Подсказка 4
Для a₃ можно воспользоваться неравенством из условия. Не забывайте, что члены последовательности — натуральные числа.
Подсказка 5
Попробуйте при помощи метода математической индукции доказать, что последовательность a задает ряд натуральных чисел.
Найдём несколько первых членов последовательности:
Так как все члены последовательности натуральны, в соответствии с полученным неравенством может принимать значения 2 и
3.
Пусть тогда
Но не существует натурального числа, лежащего между 3 и 4, следовательно, такой случай невозможен.
Получается, что в этом случае
Следовательно,
Предположим, что -тый член последовательности равен
а
-ый член последовательности равен
найдём
-ой член
последовательности:
Таким образом, методом математической индукции доказано, что данная нам последовательность — последовательность натуральных
чисел, тогда
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Подсказка 1
Как Вы думаете, что можно сделать с основанием логарифма?
Подсказка 2
Так как мы вычитаем 5, свойства логарифмов нам не помогут. А поможет ли нам новая переменная?
Подсказка 3
Пусть t = 2 ⋅ 3ˣ - 5. Выразите x.
Подсказка 4
Решите неравенство при помощи метода рационализации и не забудьте сделать обратную замену, а также учесть все ограничения для t!
Обозначим тогда
А так же
Сразу отметим, что и
После замены неравенство примет вид:
Воспользуемся методом рационализации:
Учитывая ограничения на , получаем
Остается вернуться к исходной переменной и решить систему:
Ошибка.
Попробуйте повторить позже
Решите уравнение
Источники:
Подсказка 1
Давайте для начала просто раскроем скобки.
Подсказка 2
Можно ли здесь заметить какие-то тригонометрические формулы?
Подсказка 3
Попробуйте увидеть синус разности.
Подсказка 4
Осталось просто дорешать уравнение, воспользовавшись формулой двойного угла и представив наше уравнение в виде произведения двух скобок.
Раскроем скобки в левой части уравнения:
Перегруппируем слагаемые и воспользуемся формулой синуса разности:
Распишем синус двойного угла и разложим выражение на множители:
Так как и
поделим уравнение на эту ненулевую скобку.
Ошибка.
Попробуйте повторить позже
Внутри окружности радиуса 5 отмечена точка
через которую проведены хорды
и
перпендикулярные друг другу.
Найдите все возможные значения расстояния от вершины
прямоугольника
до центра
окружности
если известно, что
Источники:
Подсказка 1
Нам ведь не просто так дана перпендикулярность, мы определенно воспользуемся ей в будущем, но как это сделать?
Подсказка 2
Скорее всего, перпендикулярность пригодится нам для теоремы Пифагора. Найти мы хотим FO, какие отрезки можно посчитать для этого?
Подсказка 3
Давайте проведем через точку O прямую, параллельную AB, тогда на этой прямой и прямой FA образуется прямоугольный треугольник с гипотенузой FO!
Подсказка 4
Все равно пока не очень понятно, как считать... Нам даны радиус и отрезок OE, но для чего?
Подсказка 5
А можно ли получить где-то равные им отрезки?
Подсказка 6
Пусть прямая, проведенная через O параллельно AB, пересекается с FA в точке X, с CE — в точке K. Обозначим KO за x, продлим KO за точку X на длину x, получим точку O₁.
Подсказка 7
Запишите теорему Пифагора для треугольников XO₁F и XAO. Можно ли выразить их через известные величины?
Подсказка 8
Сложите полученные выражения и перегруппируйте слагаемые.
Пусть расстояние от точки до прямой
равно
Проведем через точку
прямую, параллельную
на этой прямой отметим
точку
находящуюся на расстоянии
от прямой
так, чтобы точки
и
были по разные стороны от прямой
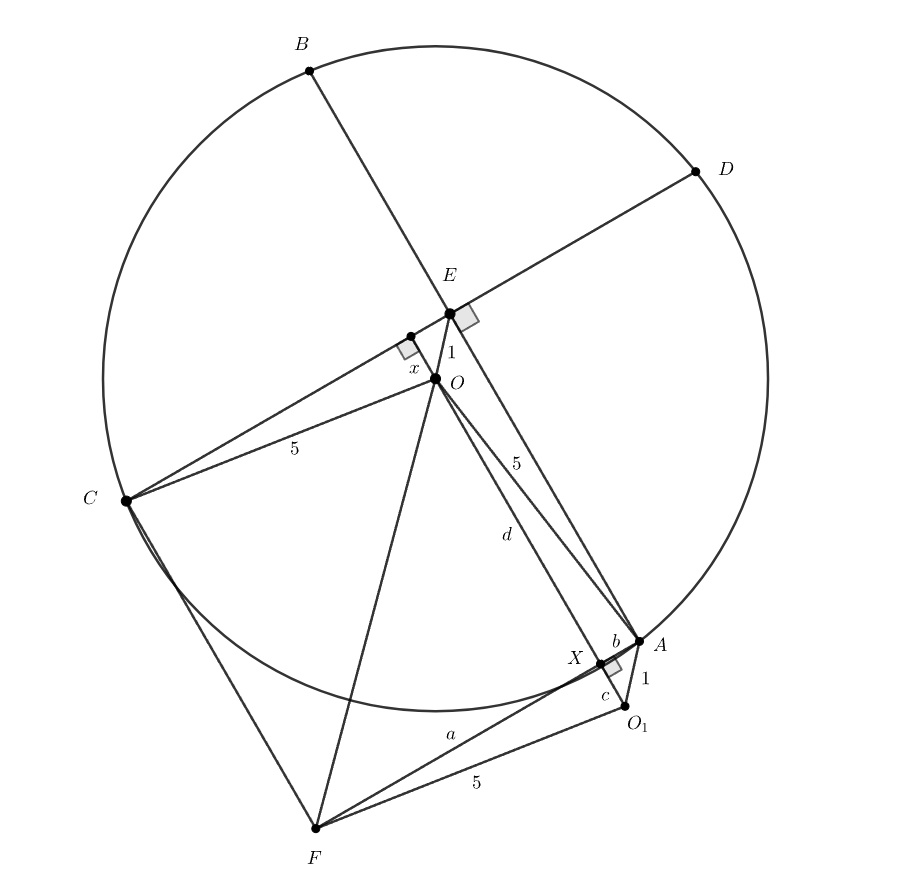
Очевидно, что и
Заметим, что диагонали четырехугольника
перпендикулярны, обозначим
точку пересечения диагоналей за
введем обозначения:
По теореме Пифагора
Отсюда можно вычислить
Ошибка.
Попробуйте повторить позже
Положительные действительные числа удовлетворяют равенству
Найдите наименьшее возможное значение
выражения
Источники:
Подсказка 1
Обратите внимание на множители (1-a), (1-b), (1-c) в числителе. Можно ли их выразить через другие переменные?
Подсказка 2
Вспомните про условие a + b + c = 1.
Подсказка 3
Есть ли какое-то известное неравенство, которое могло бы помочь оценить выражения вида √((x+y)(x+z))? Как можно применить его к нашему случаю?
Подсказка 4
Воспользуйтесь неравенством Коши-Буняковского-Шварца.
Подсказка 5
Что происходит с выражением, когда все переменные равны?
Преобразуем данное выражение с учетом равенств
и
По неравенству Коши-Буняковского-Шварца:
Получаем
Наименьшее значение выражения равно 1, и это значение достигается при



