ДВИ 2025
Ошибка.
Попробуйте повторить позже
Четырехугольник вписан в окружность. Найдите все возможные значения угла
где
и
— центры вписанных
окружностей в треугольники
и
соответственно.
Источники:
Подсказка 1
Грамотный чертеж поможет решить задачу. Рассматриваются центры вписанных окружностей разных треугольников. Какие построения могут пригодиться?
Подсказка 2
Точно! Нам нужны биссектрисы. Построим их для ∠BAC и∠BDC. Где они пересекутся? Что еще можно про них сказать?
Подсказка 3
Они пересекутся на окружности, в которую вписан ABCD, и на них расположены центры вписанных окружностей треугольников ABC и BCD. Применим лемму о трезубце, что следует из нее?
Подсказка 4
Из леммы о трезубце получим, что EX = BX = XC = FX. Проведем аналогичные действия для биссектрис ∠ACB и ∠BDA, пусть они пересекаются в точке Y. Введем обозначения для дуг AD = x и CD = y. Теперь сможем посчитать ∠XEF и ∠YEG.
Подсказка 5
XEF = 90 - x/4 и YEG = 90 - y/4. Теперь посчитаем, чему равен ∠AEC. Это угол в треугольнике между двумя биссектрисами. А чему равен ∠AEY?
Подсказка 6
Выразите его через ∠AEC. Теперь вернемся к вопросу задачи!
Проведем биссектрисы углов и
Они пересекутся в точке
лежащей на окружности. На проведенных биссектрисах будут
лежать центры вписанных окружностей
и
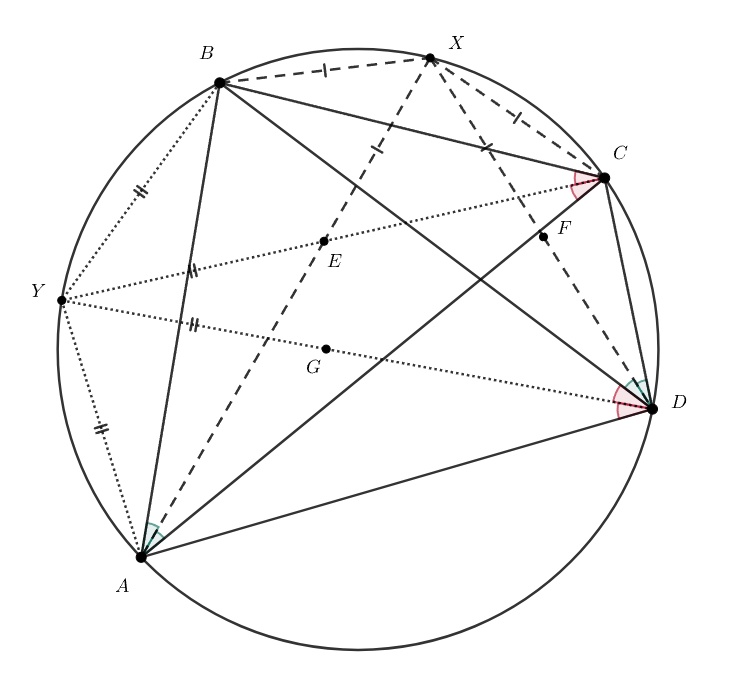
По лемме о трезубце и
следовательно,
Пусть биссектрисы
и
пересекаются в точке
лежащей на окружности. На проведенных биссектрисах будут лежать центры вписанных окружностей
и
По лемме о трезубце
Рассмотрим равнобедренные треугольники и
Пусть дуга
дуга
тогда
Поскольку
а
Аналогично,
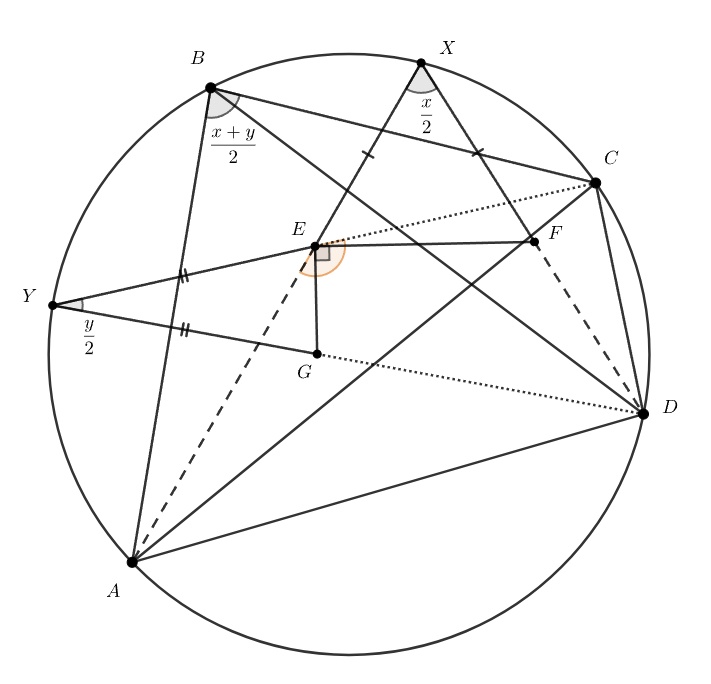
Выведем вспомогательный факт:
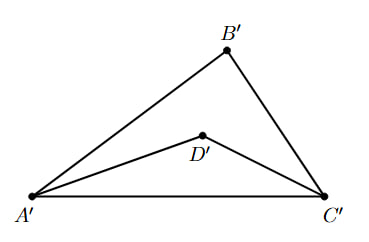
Пусть — точка пересечения биссектрис углов
И
Тогда если
то
Поскольку и
лежат на биссектрисах,
По сумме углов в треугольнике
Вернемся к исходной картинке. Рассмотрим треугольник В нем
— точка пересечения биссектрис. Тогда
Кроме того,
В итоге,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




