Функция обратной пропорциональности
Готовиться с нами - ЛЕГКО!

График какой из приведенных ниже функций изображен на рисунке?
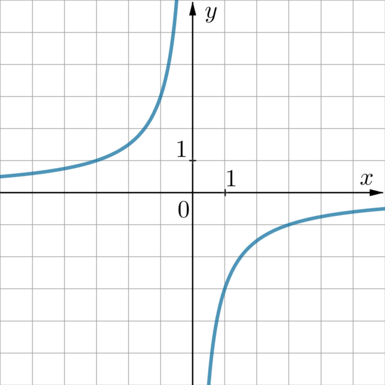
1) \(y=\dfrac 3x\qquad \) 2) \(y=-\dfrac1{3x}\qquad \) 3) \(y=\dfrac1{3x}\qquad \) 4) \(y=-\dfrac3x\)
На рисунке изображена гипербола, уравнение которой имеет вид \(y=\dfrac kx\), причем, так как она находится во 2 и 4 четвертях, то \(k<0\).
Следовательно, выбираем между 2 и 4.
Данная гипербола проходит, например, через точку \(x=-1, y=3\). Проверкой убеждаемся, что эта точка удовлетворяет уравнению 4 (подставим: \(y=-\frac3{-1}=3\)).
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
График какой из приведенных ниже функций изображен на рисунке?
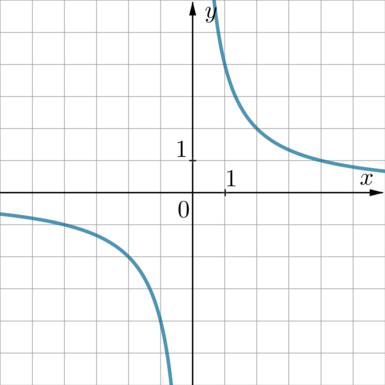
1) \(y=\dfrac 4x\qquad \) 2) \(y=-\dfrac1{4x}\qquad \) 3) \(y=-\dfrac4{x}\qquad \) 4) \(y=\dfrac1{4x}\)
На рисунке изображена гипербола, уравнение которой имеет вид \(y=\dfrac kx\), причем, так как она находится в 1 и 3 четвертях, то \(k>0\).
Следовательно, выбираем между 1 и 4.
Данная гипербола проходит, например, через точку \(x=1, y=4\). Проверкой убеждаемся, что эта точка удовлетворяет уравнению 1 (подставим \(y=\frac 41=4\)).
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
На одном из рисунков изображен график функции \(y=\dfrac3x\). Укажите номер этого рисунка.
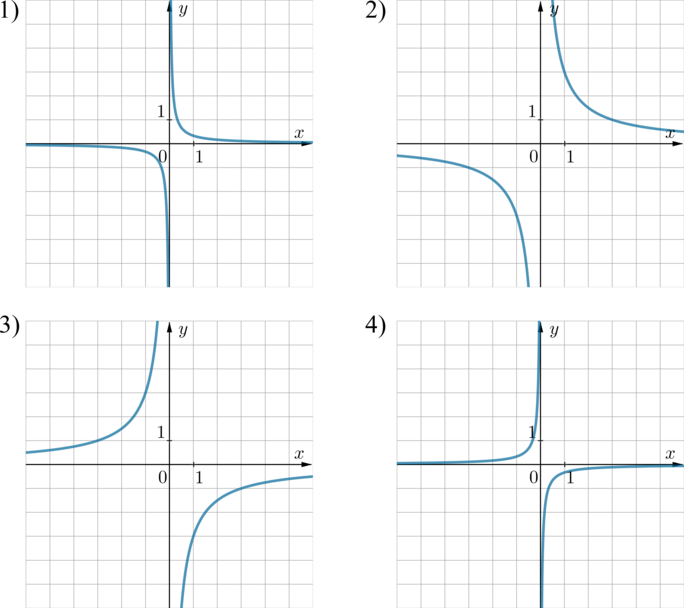
Если в уравнении гиперболы \(y=\frac kx\) коэффициент \(k>0\), то она находится в 1 и 3 четвертях, если \(k<0\) – во 2 и 4. В нашем случае гипербола \(y=\frac 3x\) находится в 1 и 3 четвертях, следовательно, либо картинка 1, либо картинка 2.
Гипербола \(y=\frac 3x\) проходит через точку \(x=1, y=3\). Через эту точку проходит только гипербола, изображенная на картинке 2.
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
На одном из рисунков изображен график функции \(y=-\dfrac5x\). Укажите номер этого рисунка.
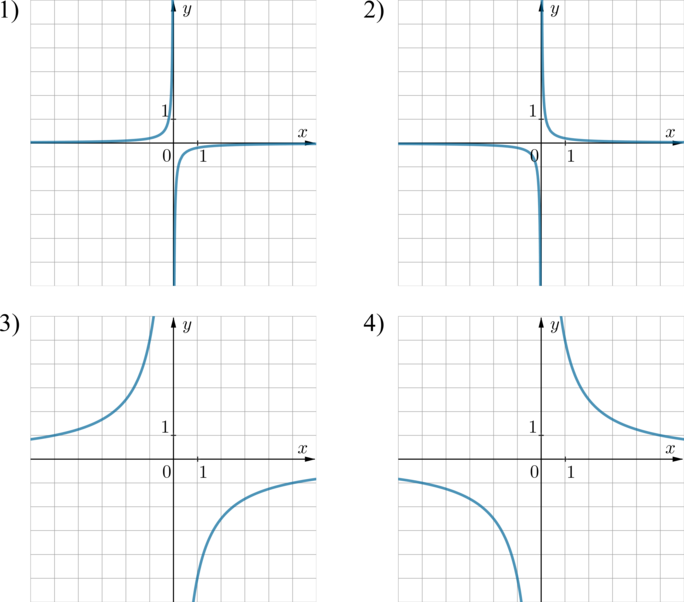
Если в уравнении гиперболы \(y=\frac kx\) коэффициент \(k>0\), то она находится в 1 и 3 четвертях, если \(k<0\) – во 2 и 4. В нашем случае гипербола \(y=-\frac 5x=\frac{-5}x\) находится во 2 и 4 четвертях, следовательно, либо картинка 1, либо картинка 3.
Гипербола \(y=-\frac 5x\) проходит через точку \(x=-1, y=5\). Через эту точку проходит только гипербола, изображенная на картинке 3.
(В данном случае достаточно было бы воспользоваться тем, через какую точку проходит гипербола.)
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ:
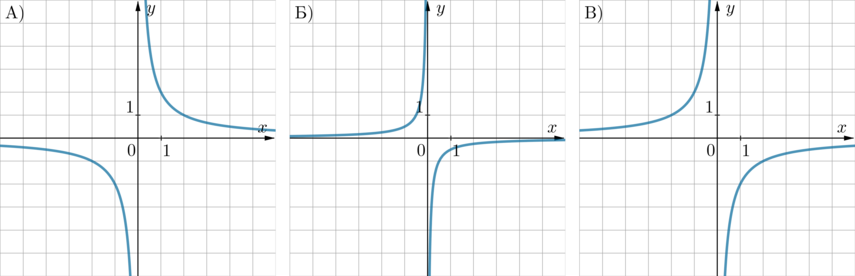
ФОРМУЛЫ:
1) \(y=-\dfrac 2x\qquad \) 2) \(y=\dfrac2x\qquad \) 3) \(y=-\dfrac1{2x}\)
В таблице под каждой буквой укажите соответствующий номер.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline && \\ \hline \end{array}\)
Способ 1.
Если в уравнении гиперболы \(y=\frac kx\) коэффициент \(k>0\), то она находится в 1 и 3 четвертях, если \(k<0\) – во 2 и 4. Отсюда следует, что гиперболе А, находящейся в 1 и 3 четвертях, соответствует формула 2.
Гипербола В проходит, например, через точку \(x=-1, y=2\). Эта точка удовлетворяет только формуле 1. Следовательно, В – 1, Б – 3.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline 2&3&1 \\ \hline \end{array}\)
В ответ запишем 231.
(Вообще говоря, в одном масштабе чем “плотнее” гипербола \(y=\frac kx\) прижата к осям координат, тем меньше по модулю ее коэффициент \(k\). Например в нашем случае масштабы всех картинок одинаковы, и на картинке Б гипербола плотнее прижата к осям, следовательно, из двух формул 1 и 3 ей соответствует формула 3, так как в формуле 1 коэффициент \(k=-2\), а в формуле 3 коэффициент \(k=-\frac12\).)
Способ 2.
Заметим, что формулы 1 и 2 отличаются лишь знаком, это значит, что график, задающийся формулой 2, получается из графика, задающегося формулой 1, отражением относительно горизонтальной оси. Такие графики у нас представлены на картинках А и В. Если в уравнении гиперболы \(y=\frac kx\) коэффициент \(k>0\), то она находится в 1 и 3 четвертях, если \(k<0\) – во 2 и 4. Отсюда однозначно: А – 2, В – 1.
Тогда Б – 3.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ:
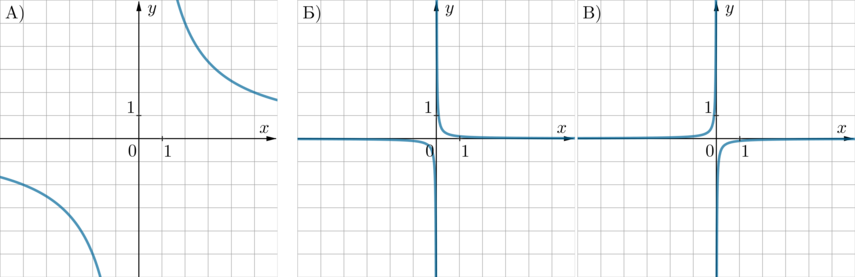
ФОРМУЛЫ:
1) \(y=\dfrac1{10x}\qquad \) 2) \(y=-\dfrac1{10x}\qquad \) 3) \(y=\dfrac{10}x\)
В таблице под каждой буквой укажите соответствующий номер.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline && \\ \hline \end{array}\)
Способ 1.
Если в уравнении гиперболы \(y=\frac kx\) коэффициент \(k>0\), то она находится в 1 и 3 четвертях, если \(k<0\) – во 2 и 4. Отсюда следует, что гиперболе В, находящейся в 2 и 4 четвертях, соответствует формула 2.
Гипербола А проходит, например, через точку \(x=2, y=5\). Эта точка удовлетворяет только формуле 3. Следовательно, А – 3, Б – 1.
Ответ: \(\begin{array}{|c|c|c|} \hline \text{А} & \text{Б} & \text{В} \\ \hline 3&1&2 \\ \hline \end{array}\)
В ответ запишем 312.
(Вообще говоря, в одном масштабе чем “плотнее” гипербола \(y=\frac kx\) прижата к осям координат, тем меньше по модулю ее коэффициент \(k\). Например в нашем случае масштабы всех картинок одинаковы, и на картинке Б гипербола плотнее прижата к осям, следовательно, из двух формул 1 и 3 ей соответствует формула 1, так как в формуле 1 коэффициент \(k=\frac1{10}\), а в формуле 3 коэффициент \(k=10\).)
Способ 2.
Заметим, что формулы 1 и 2 отличаются лишь знаком, это значит, что график, задающийся формулой 2, получается из графика, задающегося формулой 1, отражением относительно горизонтальной оси. Такие графики у нас представлены на картинках Б и В. Если в уравнении гиперболы \(y=\frac kx\) коэффициент \(k>0\), то она находится в 1 и 3 четвертях, если \(k<0\) – во 2 и 4. Отсюда однозначно: Б – 1, В – 2.
Тогда А – 3.
Найдите значение \(k\) по графику функции \(y=\dfrac kx\), изображенному на рисунке.
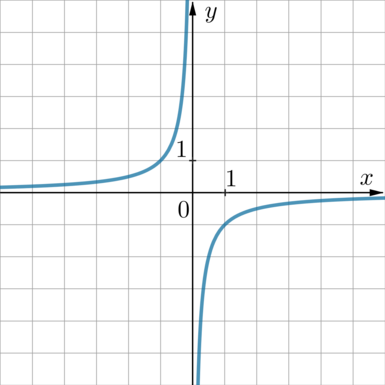
Данная гипербола проходит, например, через точку \(x=-1, y=1\). Следовательно, имеем: \(1=\frac k{-1}\), откуда \(k=-1\).



