Квадратичные неравенства
Готовиться с нами - ЛЕГКО!

Укажите множество решений неравенства \(x^2\geqslant 121\).
1) \([0;11]\)
2) \([11;+\infty)\)
3) \([-11; 11]\)
4) \((-\infty; -11]\cup[11;+\infty)\)
Способ 1. Перепишем неравенство в виде \[x^2-11^2\geqslant 0\quad\Leftrightarrow\quad (x-11)(x+11)\geqslant 0\] Решим квадратичное неравенство, схематично изобразив параболу \(y=(x-11)(x+11)\) (ветви направлены вверх, так как перед \(x^2\) положительный коэффициент):
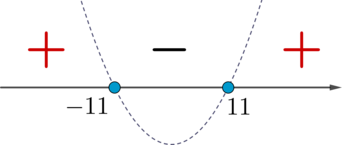
(точки пересечения с осью \(x\) закрашенные, так как знак неравенства нестрогий)
Так как знак неравенства \(\geqslant \), то выбираем “\(+\)” и закрашенные точки, следовательно, ответ \(x\in(-\infty; -11]\cup[11;+\infty)\).
Способ 2. Решим неравенство с помощью модуля: \[x^2\geqslant 11^2\quad\Leftrightarrow\quad |x|\geqslant 11 \quad\Leftrightarrow\quad x\in (-\infty; -11]\cup[11;+\infty)\]
Укажите множество решений неравенства \(x^2+11\geqslant 75\).

Способ 1. Перепишем неравенство в виде \[x^2-64\geqslant 0\quad\Leftrightarrow\quad (x-8)(x+8)\geqslant 0\] Решим квадратичное неравенство, схематично изобразив параболу \(y=(x-8)(x+8)\) (ветви направлены вверх, так как перед \(x^2\) положительный коэффициент):
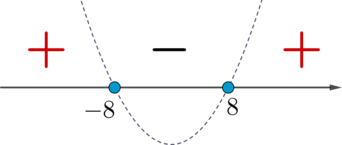
(точки пересечения с осью \(x\) закрашенные, так как знак неравенства нестрогий)
Так как знак неравенства \(\geqslant \), то выбираем “\(+\)” и закрашенные точки, следовательно, ответ \(x\in(-\infty; -8]\cup[8;+\infty)\).
Способ 2. Решим неравенство с помощью модуля: \[x^2\geqslant 8^2\quad\Leftrightarrow\quad |x|\geqslant 8 \quad\Leftrightarrow\quad x\in (-\infty; -8]\cup[8;+\infty)\]
Укажите множество решений неравенства \((x+3)(x-5)\leqslant 0\).
1) \(x\leqslant -3\), \(x\geqslant 5\)
2) \(-3\leqslant x\leqslant 5\)
3) \(-5\leqslant x\leqslant 3\)
4) \(x\leqslant 5\), \(x\leqslant -3\)
Решим квадратичное неравенство, схематично изобразив параболу \(y=(x+3)(x-5)\) (ветви направлены вверх, так как перед всеми \(x\) положительные коэффициенты):
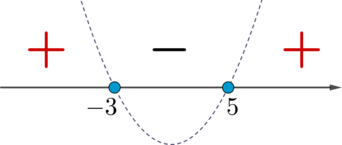
(точки пересечения с осью \(x\) закрашенные, так как знак неравенства нестрогий)
Так как знак неравенства \(\leqslant \), то выбираем “\(-\)” и закрашенные точки, следовательно, ответ \(x\in[-3;5]\). Выбираем 2.
Укажите неравенство, множество решений которого изображено на рисунке:

1) \(x^2-16\leqslant 0\)
2) \(x^2-4x\leqslant 0\)
3) \(x^2-4x\geqslant 0\)
4) \(x^2-16\geqslant 0\)
Неравенства можно переписать в следующем виде:
1) \((x-4)(x+4)\leqslant 0\)
2) \((x-4)x\leqslant 0\)
3) \((x-4)x\geqslant 0\)
4) \((x-4)(x+4)\geqslant 0\)
Так как нули на рисунке – это точки \(0\) и \(4\), то нужно выбирать между 2 и 3 неравенствами. Решим второе неравенство, схематично изобразив параболу \(y=(x-4)x\) (ветви направлены вверх, так как перед всеми \(x\) положительные коэффициенты):
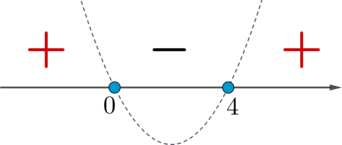
(точки пересечения с осью \(x\) закрашенные, так как знак неравенства нестрогий)
Так как знак неравенства \(\leqslant \), то выбираем “\(-\)” и закрашенные точки, следовательно, ответ \(x\in[0;4]\). На рисунке в условии изображено множество \((-\infty;0]\cup[4; +\infty)\). Следовательно, неравенство 2 не подходит, значит, ответ 3.
Укажите множество решений неравенства \(x^2-7x+12\leqslant 0\).
1) \([3;4]\)
2) \([4; +\infty)\)
3) \([-4;-3]\)
4) \((-\infty; 3]\cup[4;+\infty)\)
Найдем корни \(x^2-7x+12=0\). Можно через дискриминант, можно по теореме Виета: \(x_1+x_2=7\), \(x_1\cdot x_2=12\), откуда подбором \(x_1=3\), \(x_2=4\). Следовательно, неравенство можно переписать в виде \[(x-3)(x-4)\leqslant 0\]Решим его, схематично изобразив параболу \(y=(x-3)(x-4)\) (ветви направлены вверх, так как перед всеми \(x\) положительные коэффициенты):
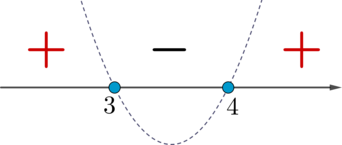
(точки пересечения с осью \(x\) закрашенные, так как знак неравенства нестрогий)
Так как знак неравенства \(\leqslant \), то выбираем “\(-\)” и закрашенные точки, следовательно, ответ \(x\in[3;4]\). Выбираем 1.
Укажите неравенство, которое не имеет решений.
1) \(x^2-14x+50<0\)
2) \(x^2-14x-50<0\)
3) \(x^2-14x+50>0\)
4) \(x^2-14x-50>0\)
Способ 1. Решим каждое неравенство. Заметим, что 1 и 3 неравенства отличаются только знаком, как и 2 и 4. Следовательно, решим только 1 и 2.
Решим \(x^2-14x+50=0\). Дискриминант \(D=196-200<0\), следовательно, корней нет. Изобразим схематично параболу \(y=x^2-14x+50\). Ее ветви направлены вверх, так как коэффициент перед \(x^2\) положительный. Она не будет пересекать ось \(x\), так как уравнение не имеет корней.

В ответ нужно записать промежутки с “\(-\)”, таких нет, следовательно, решений у неравенства нет.
Значит, ответ 1.
(Нам повезло, что 1 неравенство и оказалось нужным неравенством. В противном случае нам нужно было бы решить и 2 неравенство и записать ответы к 3 и 4 неравенствам.)
Способ 2. Чтобы квадратичное неравенство не имело решений, как минимум дискриминант квадратичного трехчлена должен быть \(\leqslant 0\) (тогда парабола будет располагаться либо выше/ниже оси \(x\) или “сидеть” на ней). Следовательно, выбор стоит между 1 и 3 неравенствами. Далее решаем, как в способе 1, оба этих неравенства. Либо решаем одно из них, и если оно не подходит, то выбираем другое.
Укажите неравенство, решением которого является любое число.
1) \(-x^2+3x-12>0\)
2) \(-x^2-3x+12>0\)
3) \(-x^2-3x+12<0\)
4) \(-x^2+3x-12<0\)
Чтобы решениями квадратичного неравенства были любые \(x\), как минимум дискриминант квадратичного трехчлена должен быть \(\leqslant
0\) (тогда парабола будет располагаться либо выше/ниже оси \(x\) или “сидеть” на ней). Следовательно, выбор стоит между 1 и 4 неравенствами (их дискриминант \(D=9-48<0\)). Решим одно из них (например, первое), и если оно не подходит, то выберем другое.
Изобразим схематично параболу \(y=-x^2+3x-12\). Ее ветви направлены вниз, так как коэффициент перед \(x^2\) отрицательный. Она не будет пересекать ось \(x\), так как уравнение не имеет корней.
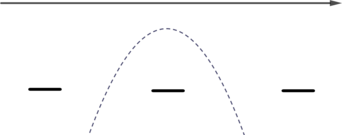
В ответ нужно записать промежутки с “\(+\)”, таких нет, следовательно, решений у неравенства нет.
Значит, ответ 1.



