Линейные неравенства (страница 2)
Готовиться с нами - ЛЕГКО!

Укажите множество решений неравенства \(4(x+3)>8\).
1) \(x<5\)
2) \(x>-1\)
3) \(x>5\)
4) \(x<-1\)
Решим неравенство \[4x+12>8\quad\Leftrightarrow\quad 4x>8-12\quad\Leftrightarrow\quad x>-1\] Ответ 2.
Укажите множество решений неравенства \(2x-3(x-4)\leqslant -7\).
1) \([-5; +\infty)\)
2) \((-\infty;-5]\)
3) \((-\infty;19]\)
4) \([19; +\infty)\)
Решим неравенство \[2x-3x+12\leqslant -7\quad\Leftrightarrow\quad -x\leqslant -7-12\quad\Leftrightarrow\quad x\geqslant 19\] Ответ 4.
Укажите множество решений неравенства \(18-5(x+3)>1-7x\).
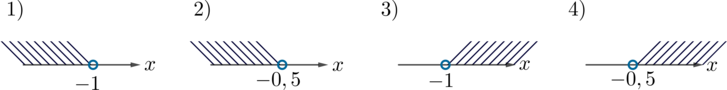
Решим неравенство \[18-5x-15>1-7x\quad\Leftrightarrow\quad -5x+7x>1-18+15\quad\Leftrightarrow\quad 2x>-2\quad\Leftrightarrow\quad x>-1\] Решения \(x\in (-1; +\infty)\), следовательно, ответ 3.
Укажите множество решений неравенства \(5x-6<4(3-x)-9x\).
1) \(x<1,8\)
2) \(x>1,8\)
3) \(x>1\)
4) \(x<1\)
Решим неравенство \[5x-6<12-4x-9x\quad\Leftrightarrow\quad 5x+13x<12+6\quad\Leftrightarrow\quad 18x<18 \quad\Leftrightarrow\quad x<1\] Ответ 4.
Укажите множество решений неравенства \(\dfrac x2-\dfrac{2-x}7\leqslant \dfrac{5x+10}{14}-\dfrac97\).
1) \(x\geqslant -1\)
2) \(x\leqslant -1\)
3) \(x\geqslant -2\)
4) \(x\leqslant -2\)
Решим неравенство. Перенесем все слагаемые в одну часть и приведем к общему знаменателю: \[\begin{aligned} &\dfrac{7x-2(2-x)-(5x+10)+9\cdot 2}{14}\leqslant 0\quad\Leftrightarrow\quad \dfrac{7x-4+2x-5x-10+18}{14}\leqslant 0 \ \Big| \cdot 14\\[2ex] &\quad\Leftrightarrow\quad4x+4\leqslant 0\quad\Leftrightarrow\quad x\leqslant -1\end{aligned}\]Следовательно, ответ 2.
Найдите наибольшее целое решение неравенства \(3x-11<5(4-2x)-2x\).
Решим неравенство \[3x-11<20-10x-2x\quad\Leftrightarrow\quad 3x+12x<20+11\quad\Leftrightarrow\quad x<\dfrac{31}{15}\] Так как \(\frac{31}{15}=2\frac1{15}\), то наибольшее целое решение этого неравенства – это \(x=2\).
Найдите наименьшее целое решение неравенства \(x-12>2(7-3x)-2x\).
Решим неравенство \[x-12>14-6x-2x\quad\Leftrightarrow\quad x+8x>14+12\quad\Leftrightarrow\quad x>\dfrac{26}9\]Так как \(\frac{26}9=2\frac89\), то наименьшее целое решение неравенства – это \(x=3\).



