Теоремы, связанными с углами (страница 4)
Готовиться с нами - ЛЕГКО!

\(AB\) – касательная к окружности, причем \(A\) – точка касания. На окружности на одинаковом расстоянии от точки \(A\) отмечены точки \(C\) и \(D\), причем дуга \(\buildrel\smile\over{CD}\), не проходящая через точку \(A\), равна \(110^\circ\). Найдите угол \(BAD\), если \(\angle BAD<\angle BAC\). Ответ дайте в градусах.
Рассмотрим картинку:
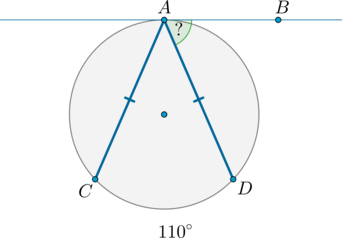
Т.к. дуги, стягиваемые равными хордами, равны, то \(\buildrel\smile\over{AC}=\buildrel\smile\over{AD}=x\). Т.к. вся окружность равна \(360^\circ\), то \(x+x+110^\circ=360^\circ\), откуда \(x=125^\circ\).
Угол \(BAD\), образованный касательной \(AB\) и хордой \(AD\), равен половине дуги, заключенной между ними, то есть \(\angle BAD=0,5 \buildrel\smile\over{AD}=62,5^\circ\).
Прямая \(AB\) касается окружности в точке \(A\). На окружности отмечена точка \(C\) так, что \(CB\perp AB\) и \(CB=AB\sqrt3\). Найдите центральный угол, опирающийся на меньшую дугу \(AC\). Ответ дайте в градусах.
Рассмотрим картинку:
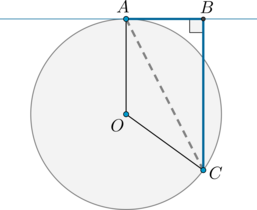
Треугольник \(ABC\) – прямоугольный, причем, т.к. \(CB=\sqrt3 \cdot AB\), то \[\mathrm{tg}\,\angle BAC=\dfrac{CB}{AB}=\sqrt3 \quad \Rightarrow \quad \angle BAC=60^\circ\]
Т.к. угол между касательной \(AB\) и хордой \(AC\) равен половине дуги \(\buildrel\smile\over{AC}\), заключенной между ними, то \(\buildrel\smile\over{AC}=120^\circ\). Тогда центральный угол \(\angle AOC=\buildrel\smile\over{AC}=120^\circ\).

