Площадь параллелограмма, ромба, прямоугольника и квадрата (страница 2)
Готовиться с нами - ЛЕГКО!

В параллелограмме \(ABCD\): \(BE\) – высота, \(BE = ED = 5\). Площадь параллелограмма \(ABCD\) равна 35. Найдите длину \(AE\).
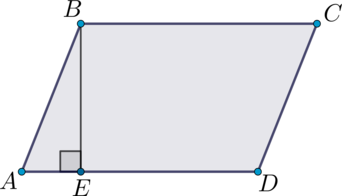
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда \(35 = BE \cdot AD = 5\cdot(5 + AE)\), откуда находим \(AE = 2\).
Периметр прямоугольника \(ABCD\) равен \(26\), а его площадь равна \(40\). Найдите разность большей и меньшей сторон этого прямоугольника.

Так как прямоугольник является частным случаем параллелограмма, то у него противоположные стороны равны.
Обозначим длину прямоугольника за \(a\), а его ширину за \(b\), тогда \(a\cdot b = 40\), \(a + b + a + b = 2(a + b) = 26\), откуда \(b = 13 - a\) и, значит, \(a \cdot (13 - a) = 40\), что равносильно \(a^2 - 13a + 40 = 0\). Дискриминант \(D = 13^2 - 4\cdot 40 = 9 = 3^2\), корни \(a_1 = 0,5(13 + 3) = 8, \ a_2 = 0,5(13 - 3) = 5\). При \(a = 5\) получаем \(b = 8\), но \(a \geq b\), тогда \(a = 8, \ b = 5\) и разность большей и меньшей сторон равна \(8 - 5 = 3\).
В прямоугольнике \(ABCD\): \(AB = \dfrac{2}{5}BC\), периметр \(ABCD\) равен \(42\). Найдите площадь треугольника \(ABC\).
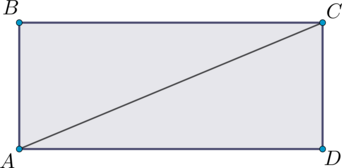
Так как прямоугольник является частным случаем параллелограмма, то у него противоположные стороны равны, тогда \(2\cdot AB + 2\cdot BC = 42\), что при \(AB = \dfrac{2}{5}BC\) равносильно \(\dfrac{4}{5}BC + 2\cdot BC = 42\), откуда находим \(BC = 15\), значит, \(AB = 6\).
Треугольники \(ABC\) и \(ADC\) равны по двум катетам, тогда их площади равны, следовательно, площадь треугольника \(ABC\) равна половине площади \(ABCD\) и равна \(0,5\cdot 6\cdot 15 = 45\).
Точка \(E\) лежит на стороне \(BC\) прямоугольника \(ABCD\). Площадь треугольника \(AED\) равна 3. Найдите площадь прямоугольника \(ABCD\).
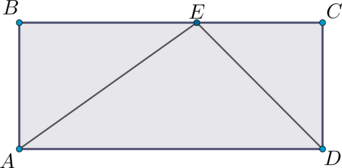
Площадь треугольника равна половине произведения основания на высоту, тогда площадь треугольника \(AED\) равна \(0,5 \cdot AD \cdot h\), где \(h\) – высота, опущенная из точки \(E\) на \(AD\). Пусть эта высота пересекает \(AD\) в точке \(F\), тогда \(FECD\) – параллелограмм (\(EF \parallel CD, \ EC \parallel FD\)), значит, \(h = CD\) и площадь прямоугольника \(ABCD\) равна \(AD \cdot h\), то есть она в два раза больше, чем площадь треугольника \(AED\) и, следовательно, равна 6.
Найдите площадь квадрата \(ABCD\), если \(AC = 10\).
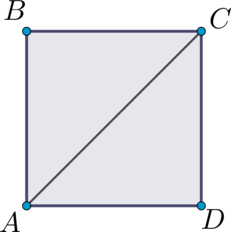
\(AD = CD\); по теореме Пифагора находим: \(AC^2 = AD^2 + CD^2 = 2\cdot AD^2\), тогда \(AD^2 = 50\), но площадь квадрата \(ABCD\) и равна \(AD^2\).
В квадрате \(ABCD\) расстояние от точки пересечения диагоналей до одной из его сторон равно \(5\). Найдите площадь этого квадрата.
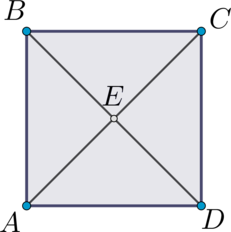
Пусть \(E\) – точка пересечения диагоналей квадрата \(ABCD\).
В квадрате диагонали равны и точкой пересечения делятся пополам, тогда \(AE = ED \ \Rightarrow \triangle ADE \) — равнобедренный.
Опустим из точки \(E\) высоту \(EF\) на \(AD\) (длина \(EF\) и есть расстояние от точки \(E\) до стороны). Так как \(\triangle ADE \) — равнобедренный, то \(EF\) является и медианой, но в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(EF = 0,5\cdot AD\).
Тогда \(AD = 10\), следовательно, площадь квадрата \(ABCD\) равна \(100\).
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

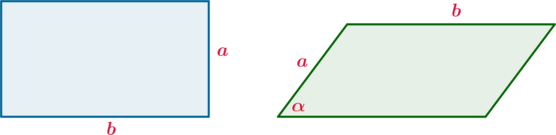
Площадь прямоугольника равна \(S_1=ab\), площадь параллелограмма равна \(S_2=ab\cdot \sin\alpha\). Из условия следует, что \(2S_2=S_1\). Следовательно: \[2ab\cdot \sin\alpha=ab\quad\Rightarrow\quad \sin\alpha=\dfrac12\quad\Rightarrow \quad \alpha=30^\circ\]



