Подобие треугольников и средняя линия треугольника
Готовиться с нами - ЛЕГКО!

На рисунке изображен колодец с “журавлем”. Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого плеча поднимется на 1 м?
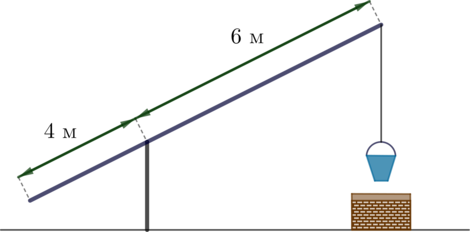
Рассмотрим чертеж колодца с “журавлем”, когда конец короткого плеча поднимется на 1 м:

Обозначим концы “журавля” в начальном положении за \(A\) и \(B\), в конечном – за \(A'\) и \(B'\). Мы получаем подобные равнобедренные треугольники \(OAA'\) и \(OBB'\). Следовательно, \[\dfrac{AA'}{BB'}=\dfrac{OA}{OB}\quad\Rightarrow\quad BB'=1,5\] (так как \(AA'=1\) по условию).
Наклонная крыша установлена на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры составляет 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры. Ответ дайте в метрах.

Заметим, что малая и большая опоры, крыша и земля образуют трапецию (в которой малая и большая опоры – это основания). Для этой трапеции средняя опора является средней линией (так как пересекает одну из боковых сторон в середине и параллельна основаниям). Так как средняя линия трапеции равна полусумме ее оснований, то длина средней опоры равна \((1,8+2,8):2=2,3\).
Наклонная крыша установлена на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры составляет 1,7 м, высота средней опоры 2,1 м. Найдите высоту большой опоры. Ответ дайте в метрах.

Заметим, что малая и большая опоры, крыша и земля образуют трапецию (в которой малая и большая опоры – это основания). Для этой трапеции средняя опора является средней линией (так как пересекает одну из боковых сторон в середине и параллельна основаниям). Так как средняя линия трапеции равна полусумме ее оснований, то \((1,7+x):2=2,1\), где \(x\) – длина большой опоры. Следовательно, из этого уравнения \(x=2,5\).
Наклонная крыша установлена на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота большой опоры составляет 2,5 м, высота средней опоры 2,2 м. Найдите высоту малой опоры. Ответ дайте в метрах.

Заметим, что малая и большая опоры, крыша и земля образуют трапецию (в которой малая и большая опоры – это основания). Для этой трапеции средняя опора является средней линией (так как пересекает одну из боковых сторон в середине и параллельна основаниям). Так как средняя линия трапеции равна полусумме ее оснований, то \((2,5+x):2=2,2\), где \(x\) – длина малой опоры. Следовательно, из этого уравнения \(x=1,9\).
Человек ростом 1,8 м стоит на расстоянии 12 м от столба, на котором висит фонарь на высоте 5,4 м. Найдите длину тени человека в метрах.
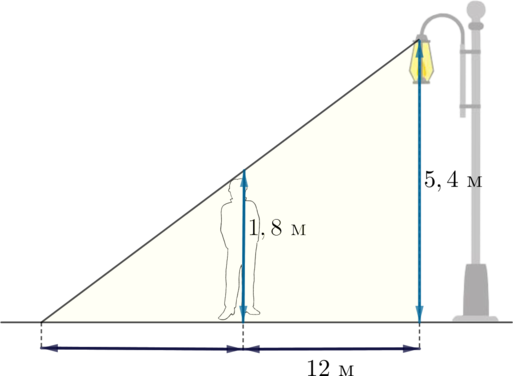
Отметим точки:
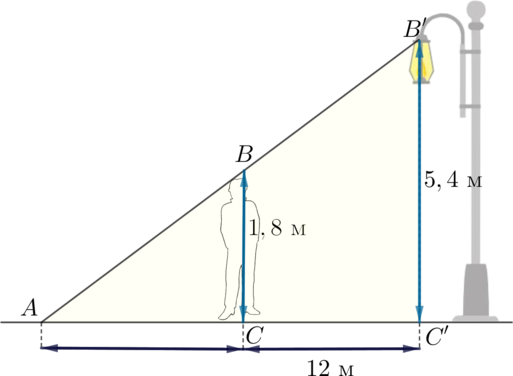
Получаем два подобных треугольника \(ABC\) и \(AB'C'\). Длина тени человека равна длине отрезка \(AC\). Тогда \[\dfrac{AC}{AC'}=\dfrac{BC}{B'C'}\quad\Rightarrow\quad
\dfrac{AC}{12+AC}=\dfrac{1,8}{5,4}\quad\Rightarrow\quad AC=6\]
На каком расстоянии в метрах от фонаря, расположенного на высоте 8 м, стоит человек ростом 2 м, если длина его тени равна 1,9 м?
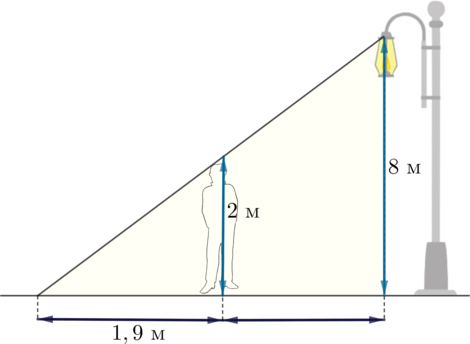
Отметим точки:
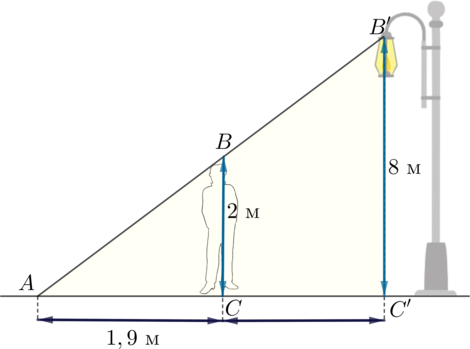
Получаем два подобных треугольника \(ABC\) и \(AB'C'\). Длина тени человека равна длине отрезка \(AC\), искомое расстояние равно длине отрезке \(CC'\). Тогда \[\dfrac{AC}{AC'}=\dfrac{BC}{B'C'}\quad\Rightarrow\quad
\dfrac{1,9}{1,9+CC'}=\dfrac{2}{8}\quad\Rightarrow\quad CC'=5,7\]
На рисунке изображен колодец с “журавлем”. Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого плеча поднимется на 1,5 м?
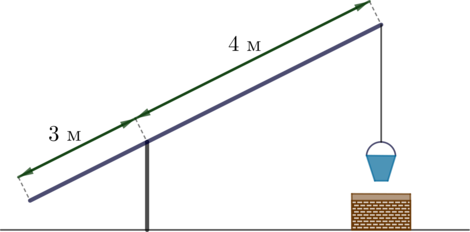
Рассмотрим чертеж колодца с “журавлем”, когда конец короткого плеча поднимется на 1,5 м:

Обозначим концы “журавля” в начальном положении за \(A\) и \(B\), в конечном – за \(A'\) и \(B'\). Мы получаем подобные равнобедренные треугольники \(OAA'\) и \(OBB'\). Следовательно, \[\dfrac{AA'}{BB'}=\dfrac{OA}{OB}\quad\Rightarrow\quad BB'=2\] (так как \(AA'=1,5\) по условию).



