Задачи по теме «Правильная и прямоугольная пирамиды»

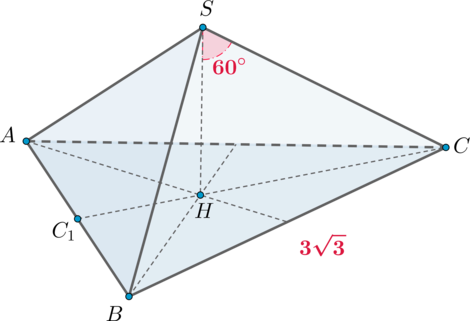
Пусть \(SH\) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис).
Пусть \(CC_1\) – высота (а значит и медиана) основания. Тогда \[CC_1=\dfrac{\sqrt3}2AB.\] Так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \[CH=\dfrac23CC_1=\dfrac{\sqrt3}3AB.\] Из прямоугольного \(\triangle SHC\): \[\mathrm{tg}\,60^\circ=\dfrac{CH}{SH}\quad\Rightarrow\quad SH=\dfrac{CH}{\sqrt3}=\dfrac13AB.\] Следовательно, объем пирамиды равен \[V=\dfrac13\cdot SH\cdot S_{ABC}=\dfrac13\cdot \dfrac13\cdot 3\sqrt3\cdot \dfrac12\cdot 3\sqrt3\cdot \dfrac{\sqrt3}2\cdot 3\sqrt3=\dfrac{27}4=6,75.\]

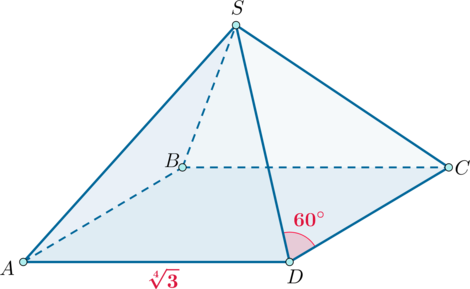
Так как пирамида правильная, то все боковые грани представляют собой равные равнобедренные треугольники. Так как у них угол при основании равен \(60^\circ\), то они являются равносторонними, то есть все боковые ребра пирамиды равны стороне основания. Площадь правильного треугольника со стороной \(a\) вычисляется по формуле \(\dfrac{\sqrt3}4a^2\), следовательно, площадь боковой поверхности \[S_{\text{бок. пов-ти}}=4\cdot \dfrac{\sqrt3}4AS^2=\sqrt3AS^2=\sqrt3\cdot \sqrt3=3.\]

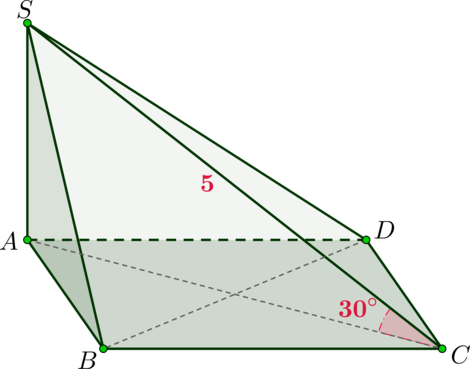
Так как \(SA\) – высота, то она перпендикулярна плоскости основания, следовательно, по определению \(AC\) является проекций \(SC\) на плоскость основания. А так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, то \(\angle SCA\) – угол между \(SC\) и основанием.
Так как \(SA\) перпендикулярна основанию, то она перпендикулярна любой прямой из основания, следовательно, \(\triangle SAC\) прямоугольный. Значит, \(AS\) как катет, лежащий против угла \(30^\circ\), равен половине \(SC\), то есть \(AS=2,5\).
По теореме Пифагора из этого же треугольника \[AC=\sqrt{SC^2-SA^2}=2,5\sqrt3.\] Так как площадь ромба равна полупроизведению диагоналей, то объем \[V=\dfrac13\cdot SA\cdot \dfrac12\cdot AC\cdot BD=25.\]

\(\triangle ABS\) и \(\triangle CBS\) – прямоугольные треугольники \(\Rightarrow\) \(SB = AB\cdot\mathrm{tg}\,60^\circ = \sqrt3\cdot\sqrt3 = 3\) \(\Rightarrow\) \(BC = SB\cdot \mathrm{ctg}\,30^\circ = 3\sqrt3\) \(\Rightarrow\) \(S_{ABCD} = \frac{1}{2}\cdot(AD + BC)\cdot AB = \frac{1}{2}\cdot(2\sqrt3 + 3\sqrt3)\cdot\sqrt3 = 7,5\) \(\Rightarrow\) \[V_{\text{пир.}} = \frac{1}{3}\cdot SB\cdot S_{ABCD} = \frac{1}{3}\cdot3\cdot7,5 = 7,5\]

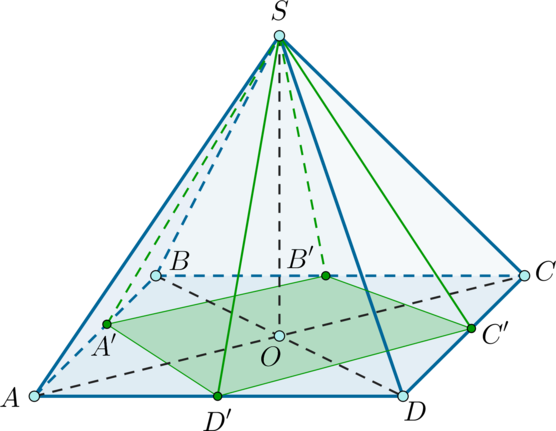
Рассмотрим рисунок. Пусть \(SABCD\) – исходная пирамида, \(A', B', C', D'\) – середины отрезков \(AB, BC, CD, DA\) соответственно. \(SO\) – высота пирамиды \(SABCD\). \[V_{SABCD}=\dfrac13\cdot SO\cdot AB^2\] Заметим, что \(SO\) – также высота пирамиды \(SA'B'C'D'\).
Так как \(ABC\) – прямоугольный треугольник, то \(AC=\sqrt{AB^2+BC^2}=\sqrt2AB\). Так как \(A'B'\) – средняя линия в \(\triangle ABC\), то \[A'B'=\frac12AC=\dfrac{\sqrt2}2AB\] Так как \(A'B'\parallel AC, A'D'\parallel BD\), а \(AC\perp BD\), то \(A'B'\perp A'D'\), следовательно, \(A'B'C'D'\) – квадрат. Следовательно, \[V_{SA'B'C'D'}=\dfrac13\cdot SO\cdot A'B'^2=\dfrac13\cdot SO\cdot \dfrac12AB^2= \dfrac12V_{SABCD}=3,5.\]

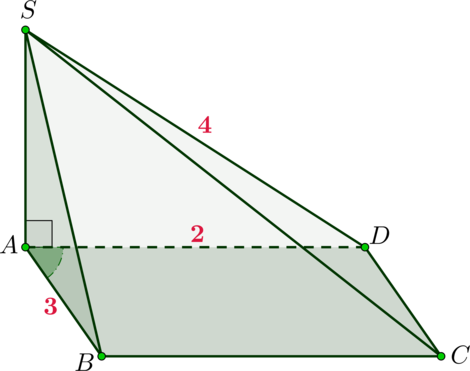
Пусть \(\angle DAB=\arcsin \dfrac{\sqrt3}4\), следовательно, \(\sin\angle DAB=\dfrac{\sqrt3}4\).

Так как \(SA\) перпендикулярно основанию, то оно перпендикулярно любой прямой из основания, следовательно, \(\triangle SAD\) – прямоугольный. Также по определению \(SA\) является высотой пирамиды. Следовательно, по теореме Пифагора \[SA=\sqrt{SD^2-AD^2}=2\sqrt3.\] Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними, следовательно, объем пирамиды равен \[V=\dfrac13\cdot SA\cdot AB\cdot AD\cdot \sin\angle DAB=3.\]

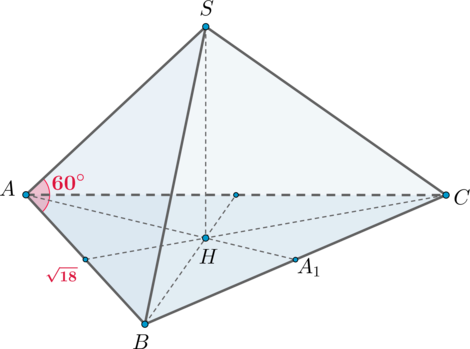
Пусть \(SH\) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис). Также боковые грани представляют собой равнобедренные треугольники. Так как в равнобедренном \(\triangle ASB\) угол при основании равен \(60^\circ\), то треугольник равносторонний, следовательно, \(AS=AB=\sqrt{18}\).
Пусть \(AA_1\) – высота основания. Следовательно, \[AA_1=\dfrac{\sqrt3}2AB.\] Так как \(AA_1\) – медиана, а медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \[AH=\dfrac23AA_1=\dfrac{\sqrt3}3AB.\] Следовательно, по теореме Пифагора \[SH=\sqrt{AS^2-AH^2}=\dfrac{\sqrt6}3AB.\] Тогда объем пирамиды равен \[V=\dfrac13\cdot SH\cdot S_{ABC}= \dfrac13\cdot \dfrac{\sqrt6}3AB\cdot \dfrac12\cdot AB\cdot \dfrac{\sqrt3}2AB=9.\]