Задачи по теме «Пирамида»
Готовиться с нами - ЛЕГКО!

Пирамида \(PA_1A_2...A_n\):
\(\blacktriangleright\) Многоугольник \(A_1...A_n\) – основание;
треугольники \(PA_1A_2, PA_2A_3\) и т.д. – боковые грани;
точка \(P\) – вершина;
отрезки \(PA_1, PA_2, ..., A_1A_2\) и т.д. – ребра.
\(\blacktriangleright\) Если в основании пирамиды лежит треугольник, то она называется тетраэдром.
\(\blacktriangleright\) Высота пирамиды – перпендикуляр, опущенный из вершины \(P\) к основанию.
\(\blacktriangleright\) Объем пирамиды \({\Large{V=\dfrac{1}{3}S_{\text{осн}}h}}\) , где \(S_{\text{осн}}\) – площадь основания, \(h\) – высота.
\(\blacktriangleright\) Площадь боковой поверхности – сумма площадей всех боковых граней.
Площадь полной поверхности – сумма площади боковой поверхности и площади основания.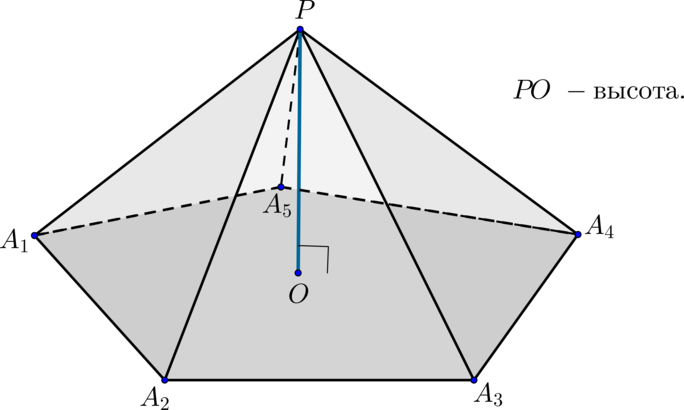
Заметим, что принято записывать название пирамиды, начиная с вершины.
Дана пирамида \(SABCD\), вершиной которой является точка \(S\), в основании лежит ромб, а высота \(SO\) пирамиды падает в точку пересечения диагоналей ромба. Найдите объем пирамиды, если известно, что угол \(ASO\) равен углу \(SBO\), а диагонали основания равны \(6\) и \(24\).
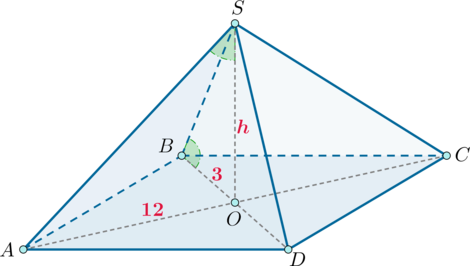
Так как диагонали ромба точкой пересечения делятся пополам, то \(AO=12\), \(BO=3\).
Заметим, что так как \(SO\) – высота пирамиды, то \(\triangle ASO\) и \(\triangle BSO\) – прямоугольные. Так как у них есть равные острые углы, то они подобны. Пусть \(SO=h\), тогда из подобия имеем: \[\dfrac{BO}{h}=\dfrac{h}{AO} \quad\Rightarrow\quad h=6.\] Так как площадь ромба равна полупроизведению диагоналей, то объем пирамиды равен \[V=\dfrac13\cdot h\cdot \dfrac12\cdot 24\cdot 6=144.\]
В пирамиде \(SABC\) высота \(SO\) падает в точку пересечения медиан основания. Треугольник \(ABC\) равнобедренный, боковые стороны равны \(10\), а основание \(AC=18\). Найдите объем пирамиды, если известно, что угол между боковым ребром \(SB\) и плоскостью основания равен \(45^\circ\).
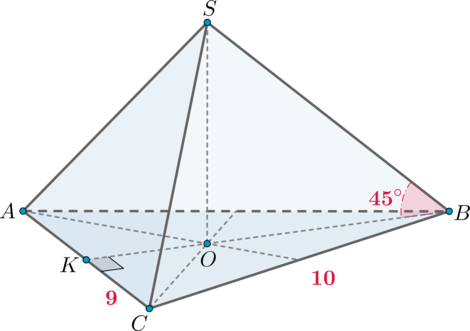
Пусть \(BK\) – высота в \(\triangle ABC\), а значит и медиана. Тогда из прямоугольного \(\triangle BKC\): \[BK=\sqrt{BC^2-KC^2}=\sqrt{10^2-9^2}=\sqrt{19}.\] Тогда площадь основания равна \[S_{ABC}=\dfrac12\cdot AC\cdot BK=9\sqrt{19}.\] Так как \(O\) – точка пересечения медиан, то \(O\) лежит на \(BK\). Так как медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины, то \[BO=\dfrac23BK=\dfrac23\sqrt{19}.\] Заметим, что угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, следовательно, \(\angle SBO=45^\circ\) и есть угол между \(SB\) и основанием (так как \(BO\) – проекция \(SB\) на плоскость \(ABC\)). Так как к тому же \(\triangle SBO\) прямоугольный, то он равнобедренный, следовательно, \[SO=BO=\dfrac23\sqrt{19}.\] Тогда объем пирамиды равен \[V=\dfrac13\cdot SO\cdot S_{ABC}=38.\]
Высота \(SH\) треугольной пирамиды \(SABC\) падает на середину стороны \(AB\), \(ABC\) – правильный треугольник со стороной \(6\). Найдите объем пирамиды, если \(SC=\sqrt{30}\).
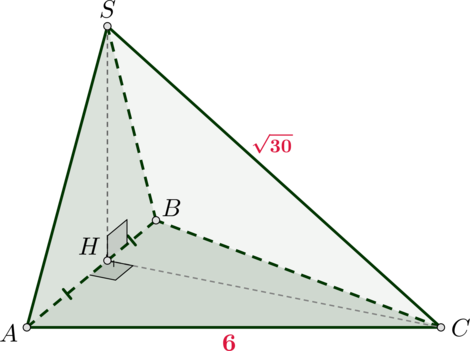
Так как \(H\) – середина \(AB\) и треугольник правильный, то \(CH\) – высота. Следовательно, \[CH=\dfrac{\sqrt3}2AB=3\sqrt3.\] Так как \(SH\) – высота пирамиды, то \(\triangle SHC\) – прямоугольный, следовательно, \[SH=\sqrt{SC^2-CH^2}=\sqrt{30-27}=\sqrt3.\] Следовательно, объем равен \[V=\dfrac13\cdot SH\cdot S_{ABC}= \dfrac13\cdot SH\cdot \dfrac12\cdot CH\cdot AB=9.\]
В основании пирамиды \(SABCD\) лежит равнобедренная трапеция \(ABCD\), \(AD\) – большее основание. Высота пирамиды падает на отрезок \(BC\). Апофема грани \(ASD\) равна \(10\) и образует угол \(45^\circ\) с плоскостью трапеции. Найдите объем пирамиды, если средняя линия трапеции равна \(9\).
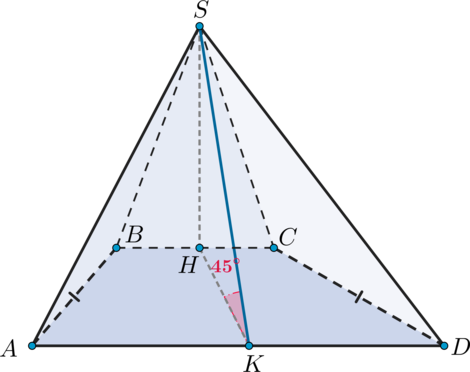
Пусть \(SH\) – высота пирамиды. Проведем \(HK\perp AD\). Следовательно, по теореме о трех перпендикулярах \(SK\) (наклонная) также перпендикулярна \(AD\) (так как \(HK\) – ее проекция на плоскость \(ABC\)). Следовательно, \(SK\) и есть апофема грани \(ASD\). Также отсюда следует, что \(\angle SKH=45^\circ\) (так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость). Следовательно, \(\triangle SHK\) прямоугольный и равнобедренный, значит, \[SH=HK=SK\div \sqrt2=\dfrac{10}{\sqrt2}\] По определению получается, что \(HK\) также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то \[S_{ABCD}=9\cdot \dfrac{10}{\sqrt2}\] А значит объем пирамиды равен \[V=\dfrac13\cdot\dfrac{10}{\sqrt2}\cdot9\cdot \dfrac{10}{\sqrt2}=150.\]
В основании пирамиды \(SABCD\) лежит равнобедренная трапеция с основаниями \(AD\) и \(BC\). \(H\) – точка пересечения диагоналей трапеции, а \(SH\) – высота пирамиды. Диагонали трапеции перпендикулярны, \(\mathrm{tg}\, \angle SAC = 3\), \(BH = 3\), \(AH = 2\). Найдите объем пирамиды.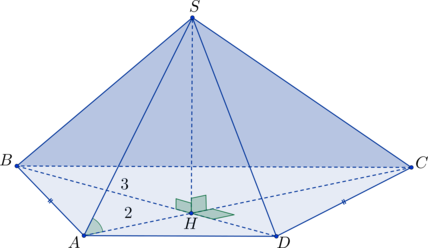
\(\triangle AHD\) и \(\triangle BHC\) – равнобедренные треугольники, т.к. трапеция \(ABCD\) равнобедренная \(\Rightarrow\) \(AH = HD\), \(BH = HC\) \(\Rightarrow\) \(AC = BD = 2 + 3 = 5\) \(\Rightarrow\)
\[S_{ABCD} = S_{ABC} + S_{ADC} = \frac{1}{2}\cdot AC\cdot BH + \frac{1}{2}\cdot AC\cdot HD = \frac{1}{2}\cdot AC\cdot(BH + HD) = \frac{1}{2}\cdot AC\cdot BD.\]
В \(\triangle SAH\): \(SH = AH\cdot \mathrm{tg}\, \angle SAC = 6\), т.к. \(\triangle SAH\) – прямоугольный. Тогда объем пирамиды можно найти следующим образом: \[V_{\text{пир.}} = \frac{1}{3}\cdot S_{ABCD}\cdot SH = \frac{1}{3}\cdot\frac{1}{2}\cdot5\cdot5\cdot6 = 25\].
В основании пирамиды \(SABC\) лежит прямоугольный треугольник с прямым углом \(\angle A\). Точка \(H\) – центр описанной вокруг треугольника \(\triangle ABC\) окружности, \(SH\) – высота пирамиды. Найдите объем пирамиды, если известно, что \(AB = 6\), \(AC = 8\), \(SA = 5\sqrt5\).
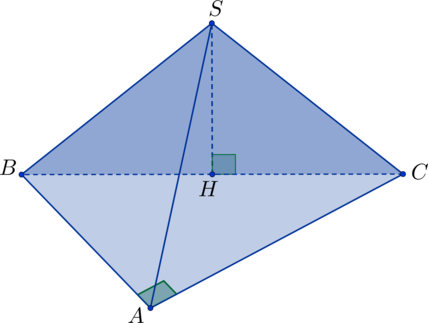
Центр описанной вокруг прямоугольного треугольника окружности лежит на гипотенузе и делит ее пополам \(\Rightarrow\) \(BH = AH = CH\) – радиусы описанной окружности. В прямоугольном треугольнике \(\triangle BAC\) по теореме Пифагора: \(BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 100\) \(\Rightarrow\) \(BC = 10\) \(\Rightarrow\) \(AH = \frac{BC}{2} = \frac{10}{2} = 5\). Треугольник \(\triangle AHS\) – прямоугольный, т.к. \(SH \perp ABC\) (\(SH\) – высота), тогда по теореме Пифагора можно найти \(SH\): \(SH^2 = AS^2 - AH^2 = (5\sqrt5)^2 - 5^2 = 100\) \(\Rightarrow\) \(SH = 10\). Теперь найдем объем пирамиды: \[V_{\text{пир.}} = \frac{1}{3}\cdot SH\cdot S_{\triangle BAC} = \frac{1}{3}\cdot SH\cdot\frac{1}{2}\cdot AB\cdot AC = \frac{1}{3}\cdot10\cdot\frac{1}{2}\cdot6\cdot8 = 80.\]
Точки \(A\), \(B\) и \(C\) лежат в плоскости \(\pi\). Прямая \(l\) образует с плоскостью \(\pi\) угол в \(45^\circ\) и проходит через точку \(B\) так, что \(\angle(l; AB) = \angle(l; BC)\). Через \(l'\) обозначим проекцию \(l\) на \(\pi\). Найдите \(\angle(l'; AB)\), если \(\angle ABC = 80^\circ\). Ответ дайте в градусах.
Докажем, что \(l'\) содержит биссектрису угла \(ABC\). Выберем на \(AB\) точку \(A'\), а на \(BC\) точку \(C'\) так, чтобы \(A'B = BC'\). Построим прямую, проходящую через точку \(B\) и точку \(H\) – середину \(A'C'\). 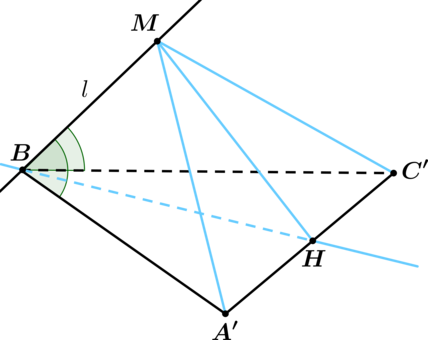
Отметим на \(l\) точку \(M\). Треугольник \(A'BC'\) – равнобедренный, тогда \(BH\) – высота.
Рассмотрим треугольники \(A'BM\) и \(C'BM\): они равны по двум сторонам и углу между ними, тогда \(MA' = MC'\) и треугольник \(A'MC'\) – равнобедренный, тогда \(MH\) – его высота.
В итоге \(A'C'\perp BH\) и \(A'C'\perp MH\), следовательно, \(A'C'\perp (MBH)\). Если предположить, что \(M'\) – проекция точки \(M\) на \((A'BC')\), не попадает на прямую, содержащую \(BH\), то получим, что \(A'C'\perp M'M\) и \(A'C'\perp MH\), откуда следует, что \(A'C'\perp (MM'H)\). Но тогда плоскости \((MM'H)\) и \((MBH)\) перпендикулярны к одной прямой, пересекаются, но не совпадают, чего быть не может.
Таким образом, \(M'\) лежит на прямой, содержащей \(BH\), но тогда \(l'\) совпадает с прямой, содержащей \(BH\). В итоге, \(\angle(l'; AB) = 0,5\angle ABC = 40^\circ\).
При подготовке к ЕГЭ по математике старшеклассникам следует особое внимание уделить теме «Пирамида», так как задачи, связанные с расчетом объема и площади данного многогранника, непременно встретятся на финальной аттестации. Весь необходимый для повторного изучения материал вы найдете в данном разделе. Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию и элементарные упражнения, а затем постепенно переходим к заданиям экспертного уровня.
Базовая информация
Пирамида — многогранник, образованный благодаря соединению всех точек плоского многоугольника с точкой, выходящей за пределы плоскости данного многоугольника.
Пирамиду называют n-угольной по количеству углов в основании. Если последним является правильный многоугольник, а основание высоты совпадает с его центром, фигуру называют правильной.
Все боковые грани пирамиды — треугольники.
Подробная теоретическая часть приведена в начале страницы. Вы также можете сразу приступить к практике. Задачи, представленные в данном разделе, помогут вам найти объем пирамиды, длину ее определенных отрезков и т. д. Каждое упражнение содержит подробный алгоритм решения и правильный ответ. Таким образом, разобраться в теме вы сможете самостоятельно, без помощи репетитора.
Как часто следует тренироваться?
Чтобы на ЕГЭ ребенок смог легко решить задачи по стереометрии (а определение площади и других параметров пирамиды относятся к данному разделу геометрии), мы рекомендуем выполнять по 2—3 упражнения каждый день. Таким образом, знания будут лучше усваиваться и вам будет проще переходить от простого к сложному.
Проверьте, легко ли вы рассчитаете площадь пирамиды, прямо сейчас. Разберите любое задание онлайн. Если решение дастся вам легко, значит, шансы на высокие экзаменационные баллы по математике достаточно велики. А при возникновении затруднений планируйте свой день таким образом, чтобы в ежедневное расписание был включен дистанционный образовательный проект «Школково». Мы поможем вам восполнить пробелы в знаниях!



