Задачи по теме «Сфера и шар»

\(\displaystyle V_{\text{шара}} = \frac{4}{3}\pi R^3 = \frac{36}{\sqrt\pi}\) \(\Rightarrow\) \(\displaystyle R = \frac{3}{\sqrt\pi}\). Радиус нового шара равен: \(\displaystyle R_{\text{нов.}} = R + \frac{6}{\sqrt\pi} = \frac{9}{\sqrt\pi}\). Тогда найдем площадь поверхности: \(\displaystyle {S_{\text{пов.}} = 4\pi R_{\text{нов.}}^2 = 4\pi \left(\frac{9}{\sqrt\pi}\right)^2 = 4\pi\frac{81}{\pi} = 324}.\)

Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна \(H = \frac{1}{2}R\)

\[\frac{V_{\text{шара}}}{V_{\text{сегм.}}} = \frac{\frac{4}{3}\pi R^3}{\pi \left(\frac{1}{2}R\right)^2\left(R - \frac{1}{3}\left(\frac{1}{2}R\right)\right)} = \frac{\frac{4}{3}\pi R^3}{\frac{5}{24}\pi R^3} = \frac{4}{3} \cdot \frac{24}{5} = \frac{32}{5} = 6,4.\]

Пусть \(V_1\) – объём шара, ограниченного первой сферой. Так как радиус \(S_1\) в два раза больше, чем радиус \(S_2\), то \(V_1 : V_2 = 8\).



\[V = V_1 - V_2 = 8V_2 - V_2 = 7V_2\,,\] следовательно, \(V : V_2 = 7\).

Т.к. площадь поверхности сферы ищется по формуле \(S=4\pi R^2\), то

\[4\pi R^2=\dfrac{37}{\pi} \quad \Rightarrow \quad R^2=\dfrac{37}{4\pi^2}\]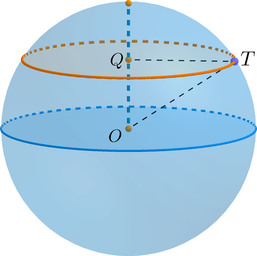

По условию задачи \(OQ=\frac1{2\pi}\). Рассмотрим \(\triangle OQT\): он прямоугольный (\(\angle OQT=90^\circ\)), гипотенуза \(OT=R\), катет \(QT\) равен радиусу \(r\) окружности сечения.

Таким образом, по теореме Пифагора \[QT^2=r^2=OT^2-OQ^2=\dfrac{37}{4\pi^2}-\dfrac1{4\pi^2}=\dfrac{9}{\pi^2} \quad \Rightarrow \quad r=\dfrac3{\pi}\]

Таким образом, длина окружности сечения равна \[C=2\pi r=2\pi\cdot\frac3{\pi}=6.\]

Т.к. площадь поверхности сферы ищется по формуле \(S=4\pi R^2\), то

\[4\pi R^2=64 \quad \Rightarrow \quad R^2=\dfrac{64}{4\pi}\]

По условию задачи \(OQ=\frac3{2\sqrt{\pi}}\). Рассмотрим \(\triangle OQT\): он прямоугольный (\(\angle OQT=90^\circ\)), гипотенуза \(OT=R\), катет \(QT\) равен радиусу \(r\) окружности сечения.

Таким образом, по теореме Пифагора \[QT^2=r^2=OT^2-OQ^2=\dfrac{64}{4\pi}-\dfrac9{4\pi}=\dfrac{55}{4\pi}\]

Таким образом, площадь сечения равна

\[S=\pi\cdot r^2=\pi\cdot \dfrac{55}{4\pi}=\dfrac{55}4=13,75.\]

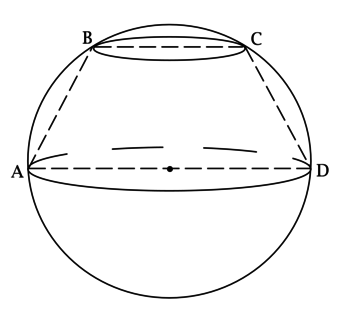
Рассмотрим \(ABCD\): т.к. \(BC\parallel AD\), то \(ABCD\) – трапеция. Так как \(AB\) и \(CD\) – образующие усечённого конуса, то \(AB = CD\) и трапеция \(ABCD\) – равнобедренная.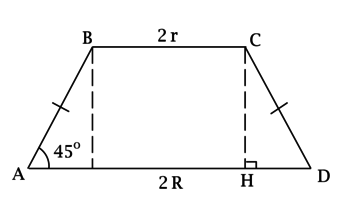

Построим \(CH\perp AD\). Так как \(\angle ADC = 45^\circ\), то \(\triangle CHD\) – равнобедренный и \(CH = HD\).
\[HD = \dfrac{AD - BC}{2} = R - r,\qquad\qquad S_{ABCD} = \dfrac{BC + AD}{2}\cdot CH = (R + r)(R - r) = R^2 - r^2 = \dfrac{210}{\sqrt[3]{\pi^2}},\] но \(r = \dfrac{R}{\sqrt{15}}\), тогда \[R^2\left(1-\dfrac{1}{15}\right) = \dfrac{210}{\sqrt[3]{\pi^2}}\qquad\Rightarrow\qquad R = \dfrac{15}{\sqrt[3]{\pi}}\qquad\Rightarrow\qquad V_{\text{шара}} = \dfrac{4}{3}\pi R^3 = \dfrac{4}{3}\cdot\pi\cdot\dfrac{15^3}{\pi} = 4500.\]

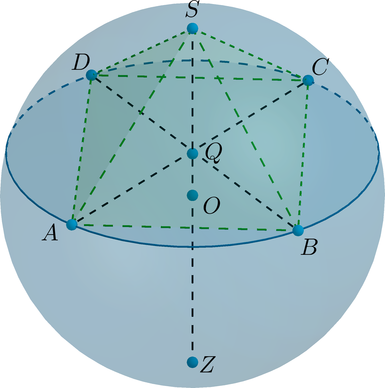
Пусть \(O\) – центр шара, \(Q\) – точка пересечения \(SZ\) и плоскости \(\alpha\). Пусть \(SABCD\) – пирамида, объем которой нужно найти.
Рассмотрим сечение шара плоскостью \(ASC\).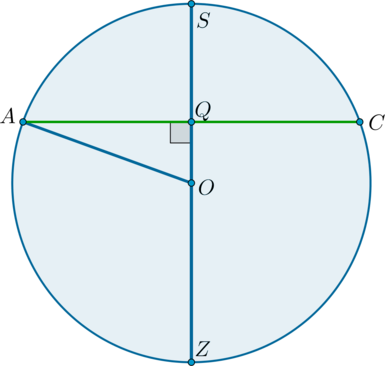



Так как \(SQ:QZ=1:2\), то \(SQ:SZ=1:3\), следовательно, \(SQ:SO=2:3\), следовательно, \(OQ:SO=1:3\). Тогда \[AQ=\sqrt{AO^2-OQ^2}=\sqrt{AO^2-\left(\dfrac13AO\right)^2}=\dfrac{2\sqrt2}3AO =\dfrac{2\sqrt2}3\cdot \dfrac92=3\sqrt2\] Следовательно, \(AC=6\sqrt2\). Следовательно, \(AB=AC:\sqrt2=6\).
Также \[SQ=\dfrac23SO=\dfrac23\cdot \dfrac92=3\] Заметим, что \(SQ\) – высота пирамиды, так как \(SQ\perp \alpha\). Следовательно, \[V=\dfrac13\cdot SQ\cdot AB^2=36.\]