Задачи по теме «Сфера и шар» (страница 2)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Сфера – это множество точек пространства, находящихся на одинаковом расстоянии от заданной точки \(O\) (называемой центром сферы).
\(\blacktriangleright\) Шар – это сфера вместе со своей внутренностью.
Основные формулы (где \(R\) – радиус сферы или шара):
\(\blacktriangleright\) площадь сферы \({\large{S=4\pi R^2}}\)
\(\blacktriangleright\) объем шара \({\large{V=\dfrac{4}{3}\pi R^3}}\)
Две параллельные плоскости перпендикулярны диаметру шара и пересекают его в точках \(A\) и \(B\). Расстояние от центра шара до этих точек равно трети и двум третям радиуса соответственно. Найдите объем шарового слоя, заключенного между этими плоскостями, деленный на \(\pi\), если радиус шара равен \(6\).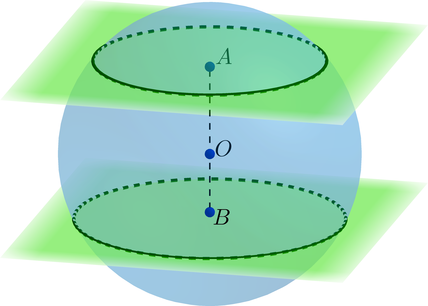
Если расстояние от центра сферы до точки \(A\) равно трети радиуса, то высота соответствующего отсекаемого сегмента равна \(R - \frac{1}{3}R = \frac{2}{3}R\).
Аналогично высота сегмента отсекаемого другой плоскостью будет равна \(R - \frac{2}{3}R = \frac{1}{3}R\).
Чтобы найти объем шарового слоя, необходимо из объема шара вычесть объемы сегментов. Воспользуемся необходимыми формулами и подсчитаем искомый объем: \[\begin{multline*}
V_{\text{слоя}} = V_{\text{шара}} - V_{\text{сегм.}A} - V_{\text{сегм.}B} =\\= \frac{4}{3}\pi R^3 - \pi \left(\frac{2}{3}R\right)^2 \left(R - \frac{1}{3}\left(\frac{2}{3}R\right)\right) - \pi \left(\frac{1}{3}R\right)^2 \left(R - \frac{1}{3}\left(\frac{1}{3}R\right)\right) =\\[4pt]
= \pi R^3 \left(\frac{4}{3} - \frac{4}{9}\left(1 - \frac{2}{9}\right) - \frac{1}{9}\left(1 - \frac{1}{9}\right)\right) = \pi R^3 \left(\frac{4}{3} - \frac{28}{81} - \frac{8}{81}\right) = \pi R^3 \frac{108 - 36}{81} =\\[4pt]
= \pi R^3 \frac{72}{81} = \frac{8}{9} \pi R^3 = \frac{8}{9} \pi 6^3 = 192\pi.
\end{multline*}\] Делим полученный результат на \(\pi\) и получаем окончательный результат.
Евгений изучает сферу. Он решил расположить её так, чтобы её центр совпал с началом прямоугольной системы координат \(Oxyz\). Плоскости \(Oxy\), \(Oyz\) и \(Oxz\) пересекли рассматриваемую сферу по большим окружностям. Евгений заметил, что если разрезать сферу по этим окружностям, то она распадётся на несколько криволинейных треугольников. Количество треугольников, на которые распадётся сфера, он обозначил через \(\Gamma\). Но сферу он разрезать не стал.
Затем Евгений посчитал число точек на сфере, через которые прошли хотя бы две из этих окружностей, он назвал эти точки вершинами, а полученное число обозначил через \(B\). Напоследок он посчитал число криволинейных отрезков на сфере, соединяющих соседние вершины (каждый такой отрезок представляет собой четверть дуги одной из полученных больших окружностей) и обозначил его через \(P\). Найдите \(\chi = \Gamma + B - P\).
При разрезании сфера распалась бы на \(8\) треугольников, то есть \(\Gamma = 8\).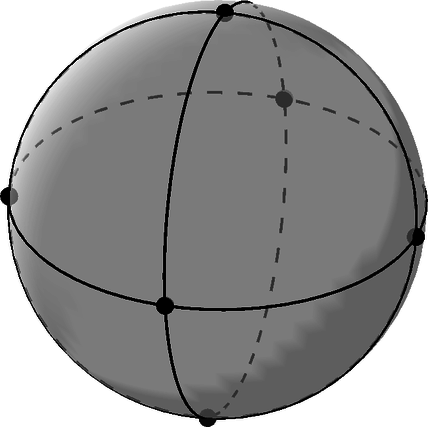
Назовём отрезки, соединяющие соседние вершины, рёбрами. Число вершин равно \(6\), то есть \(B = 6\). При этом каждая из трёх полученных больших окружностей состоит из четырёх рёбер (и вершин, но их мы уже посчитали), следовательно, \(P = 12\), тогда \[\chi = 8 + 6 - 12 = 2\,.\]
Замечание
Полученное в данной задаче число \(\chi\) называется эйлеровой характеристикой двумерной сферы. По аналогии можно рассматривать эйлеровы характеристики и у других поверхностей.
Точка \(D\) – центр сферы, точка \(A\) – центр круга \(L\), полученного в результате сечения этой сферы плоскостью. Точка \(B\) лежит на \(L\), \(AB\parallel CD\), где \(C\) – точка на сфере. Площадь \(L\) равна \(100\), \[S_{ABCD} = \dfrac{240}{\pi\sqrt{3}},\] \(\angle ADB = 30^\circ\). Найдите площадь сферы.
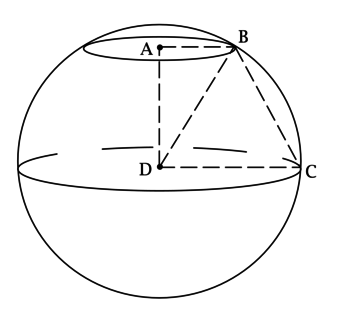
Так как \(AB\parallel CD\), а \(A\) – центр круга \(L\), \(D\) – центр сферы, то \(AD\perp AB\) и \(AD\perp DC\), тогда \(ABCD\) – прямоугольная трапеция, \[S_{ABCD} = \dfrac{1}{2}\cdot(AB + CD)\cdot AD = \dfrac{R + r}{2}\cdot h,\] где \(R\) – радиус сферы, \(r\) – радиус \(L\), \(h = AD\).
\(S_{L} = \pi r^2 = 100\), тогда \(r = \dfrac{10}{\pi}\). Рассмотрим прямоугольный треугольник \(DAB\):
т.к. \(\angle ADB = 30^\circ\), то \(AB = AD\cdot\mathrm{tg}\,
30^\circ\), откуда \[r = \dfrac{h}{\sqrt{3}}\qquad\Rightarrow\qquad h
= r\sqrt{3} = \dfrac{10\sqrt{3}}{\sqrt{\pi}}.\] \(S_{ABCD} = \dfrac{R
+ r}{2}\cdot h = \dfrac{240}{\pi\sqrt{3}}\), откуда \(R =
\dfrac{480}{h\pi\sqrt{3}} - r =
\dfrac{480\sqrt{\pi}}{10\sqrt{3}\cdot\pi\sqrt{3}} -
\dfrac{10}{\sqrt{\pi}} = \dfrac{6}{\sqrt{\pi}}\). \[S_{\text{сферы}} = 4\pi R^2 = \dfrac{4\pi\cdot 36}{\pi} = 144.\]


