Произвольная трапеция
Готовиться с нами - ЛЕГКО!

Сумма внутренних углов любого четырехугольника равна \(360^\circ\).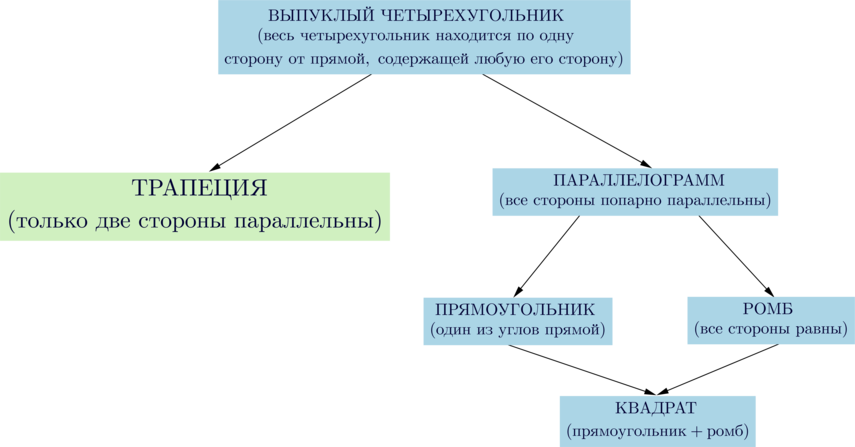
Свойства трапеции:
\(\blacktriangleright\) Сумма углов при боковой стороне равна \(180^\circ\).
\(\blacktriangleright\) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.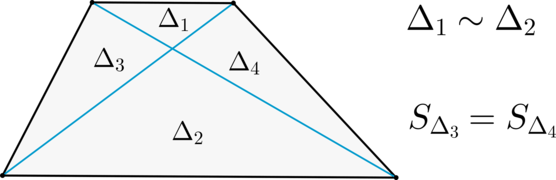
\(\blacktriangleright\) Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Одно из оснований трапеции в \(5\) раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?
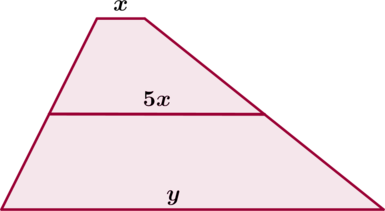
Обозначим меньшее основание трапеции за \(x\), большее – за \(y\). Тогда \(5x\) – длина средней линии трапеции. Так как средняя линия равна полусумме оснований, то \[x+y=2\cdot 5x\quad\Leftrightarrow\quad y=9x.\] Следовательно, меньшее основание в 9 раз меньше большего.

В трапеции \(ABCD\): \(CD = BC\), \(\angle BCD = 140^\circ\), \(\angle ABD = 100^\circ\). Найдите модуль разности острых углов трапеции.
\(\triangle BCD\) – равнобедренный \(\Rightarrow\) \(\angle CBD = \angle CDB = 20^\circ\); \(\angle BAD = 180^\circ - \angle ABD - \angle CBD = 180^\circ - 100^\circ - 20^\circ = 60^\circ\); \(\angle ADC = 180^\circ - 140^\circ = 40^\circ\). Тогда \(|\angle ADC - \angle BAD| = |40^\circ - 60^\circ| = |-20^\circ| = 20^\circ\).
В трапеции \(ABCD\) с основаниями \(BC = 5\) и \(AD = 2\cdot BC\) проведена высота \(BE\). Найдите отношение площади трапеции к длине этой высоты.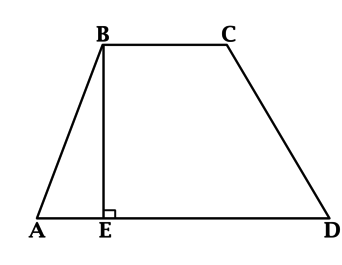
Площадь трапеции равна произведению полусуммы оснований на высоту. Полусумма оснований трапеции \(ABCD\) равна \(0,5(5 + 2\cdot 5) = 7,5\). Площадь трапеции \(ABCD\) равна \(7,5 BE\), тогда \(\dfrac{S_{ABCD}}{BE} = 7,5\).
В трапеции \(ABCD\) с основаниями \(BC = 4\) и \(AD > BC\) угол \(A\) – прямой. Известно, что \(CD = 6\), \(\angle D = 60^{\circ}\). Найдите среднюю линию трапеции \(ABCD\).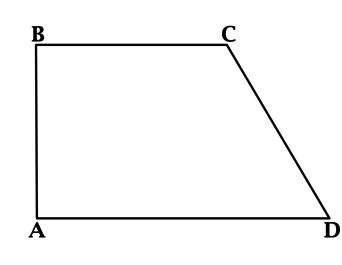
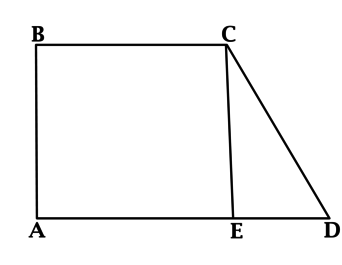
Из точки \(C\) опустим высоту \(CE\). В прямоугольном треугольнике \(CDE\): \(\angle ECD = 30^{\circ}\). В прямоугольном треугольнике катет, лежащий против угла в \(30^{\circ}\) равен половине гипотенузы, тогда \(DE = 0,5\cdot CD = 3\). При этом \(ABCE\) – прямоугольник, \(AE = BC = 4\), тогда \(AD = AE + ED = 4 + 3 = 7\).
В трапеции средняя линия равна полусумме оснований. \(0,5(BC + AD) = 0,5(4 + 7) = 5,5\), значит, длина средней линии равна \(5,5\).
В трапеции \(ABCD\) средняя линия составляет \(\dfrac{4}{5}\) одного из оснований. Найдите отношение длины другого основания к длине средней линии.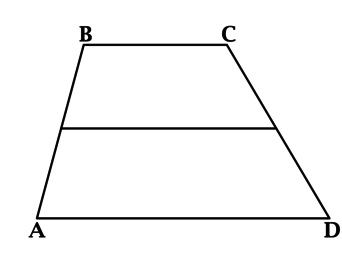
Средняя линия трапеции равна полусумме оснований. Полусумма оснований трапеции \(ABCD\) составляет \(0,8\) одного из оснований, тогда сумма оснований трапеции \(ABCD\) составляет \(2\cdot 0,8 = 1,6\) этого основания, обозначим его за \(AD\). Тогда \(BC + AD = 1,6AD\), откуда \(BC = 0,6AD\). Средняя линия равна \(0,8AD\), тогда отношение длины основания \(BC\) к длине средней линии равно \(0,6 : 0,8 = 0,75\).
Основания \(AD\) и \(BC\) трапеции \(ABCD\) равны соответственно \(20\) и \(12\), одна из боковых сторон равна \(10\), площадь трапеции \(ABCD\) равна \(80\). Найдите острый угол трапеции \(ABCD\), который образует эта боковая сторона с одним из оснований. Ответ дайте в градусах.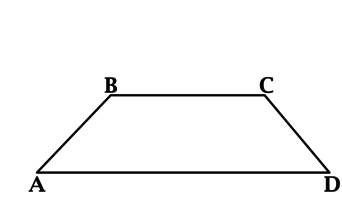
Пусть \(AB = 10\), \(BE\) – перпендикуляр к \(AD\), точка \(E\) лежит на \(AD\).
Площадь трапеции равна произведению полусуммы оснований на высоту, тогда \(80 = 0,5(20 + 12)\cdot BE\).
\(BE = 5 = 0,5\cdot AB\). Треугольник \(ABE\), – прямоугольный, причём \(BE = 0,5\cdot AB\), тогда угол, лежащий против катета \(BE\), равен \(30^{\circ}\).
\(\angle BAE = 30^{\circ}\) – единственный острый угол трапеции \(ABCD\), который образует \(AB\) с одним из оснований.

В трапеции \(ABCD\) диагонали пересекаются в точке \(O\). Площадь \(\triangle AOD\) относится к площади \(\triangle ODC\), как \(8:3\). В каком отношении состоит меньшее основание \(BC\) трапеции \(ABCD\) к большему основанию \(AD\)?
Высота, опущенная из вершины \(D\) на сторону \(AO\) в \(\triangle AOD\) и на сторону \(OC\) в \(\triangle ODC\) будет одной и той же. Значит, \(\frac{S_{\triangle DOC}}{S_{\triangle AOD}} = \frac{OC}{AO} = \frac{BC}{AD} = \frac{3}{8} = 0,375\).
Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как подготовиться к экзамену?
Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.
Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».
«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.



