Признаки и свойства равнобедренной трапеции (страница 3)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Равнобедренная трапеция – трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
\(\blacktriangleright\) Углы при каждом основании равны;
\(\blacktriangleright\) Диагонали равны;
\(\blacktriangleright\) Два треугольника, образованные диагоналями и одним из оснований, являются равнобедренными;
\(\blacktriangleright\) Два треугольника, образованные диагоналями и боковой стороной, равны.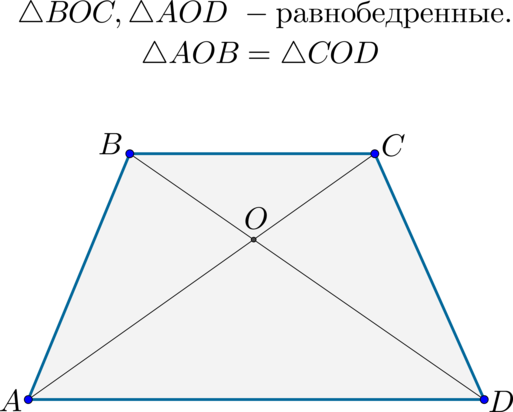
Основания равнобедренной трапеции равны \(15\) и \(9\), один из углов равен \(45^\circ\). Найдите высоту трапеции.

\(\angle A=45^\circ\). Проведем высоту \(BH\).

По свойству равнобедренной трапеции \(AH=(AD-BC):2=(15-9):2=3\). В прямоугольном \(\triangle ABH\) \(\angle
ABH=90^\circ-45^\circ=45^\circ\). Следовательно, \(\triangle ABH\) равнобедренный и \(BH=AH=3\).
Большее основание равнобедренной трапеции равно \(25\). Боковая сторона равна \(3\). Синус острого угла равен \(\frac{\sqrt{11}}6\). Найдите меньшее основание.

Проведем две высоты \(CK\) и \(DH\). По свойству равнобедренной трапеции \(HDCK\) – прямоугольник, то есть \(KH=CD=x\). Тогда \(AH+BC=25-x\), откуда \[AH=\dfrac{25-x}2\] 
Так как \(\sin\angle A=\frac{\sqrt{11}}6\), то \[\cos \angle
A=\sqrt{1-\dfrac{11}{36}}=\dfrac56\] Следовательно, из \(\triangle
ADH\): \[\dfrac56=\cos \angle A=\dfrac{AH}{AD}\quad\Rightarrow\quad
x=20\]

