Геометрия на плоскости (планиметрия). Часть II
Готовиться с нами - ЛЕГКО!

В треугольнике \(ABC\): \(\angle C = 90^{\circ}\), \(\sin {\angle BAC} = \dfrac{2}{3}\). Найдите \(AC\), если \(AB = 6\sqrt{5}\).
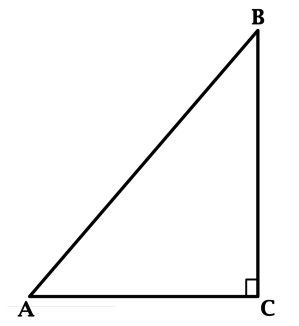
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда \[\dfrac{BC}{AB} = \dfrac{2}{3}\qquad\Rightarrow\qquad BC = \dfrac{2}{3}AB = 4\sqrt{5}.\]
По теореме Пифагора \(AC^2 = AB^2 - BC^2 = 36\cdot 5 - 16\cdot 5 = 20\cdot 5 = 10^2\), тогда \(AC = 10\).
Дан прямоугольный треугольник \(ABC\), причем \(\angle C=90^\circ\). Известно, что \(\cos \angle B=\dfrac13\), \(AB=9\). Найдите \(BC\).

По определению косинуса \[\cos\angle B=\dfrac{BC}{AB}=\dfrac13 \quad \Leftrightarrow \quad BC=\dfrac13\cdot AB=\dfrac13\cdot 9=3\]
Дан треугольник \(ABC\), причем \(\angle C=90^\circ\). Найдите длину его гипотенузы, если \(AC=8, \ \cos \angle A=\dfrac45\).

По определению косинуса \[\cos \angle A=\dfrac{AC}{AB}=\dfrac45 \quad \Leftrightarrow \quad AB=AC\cdot \dfrac54=10\]
Большее основание равнобедренной трапеции равно \(34\). Боковая сторона равна \(14\). Синус острого угла равен \(\dfrac{2\sqrt{10}}7\). Найдите меньшее основание.

Проведем \(BH\perp AD\). Из \(\triangle ABH\): \[\dfrac{2\sqrt{10}}7=\sin\angle A=\dfrac{BH}{AB}\quad\Rightarrow\quad BH=4\sqrt{10}\] Тогда по теореме Пифагора \[AH=\sqrt{14^2-(4\sqrt{10})^2}=6\] Так как \(AH=0,5(AD-BC)\), то \(BC=AD-2AH=34-12=22\).
В треугольнике \(ABC\) угол \(C=90^\circ\), \(CH\) – высота, \(AB=13\), \(\mathrm{tg}\,\angle A=0,2\). Найдите \(AH\).
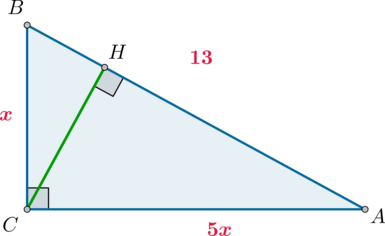
Так как по определению из \(\triangle ABC\): \[\dfrac{BC}{AC}=\mathrm{tg}\,\angle A=\dfrac 15\] то можно принять \(BC=x\), \(AC=5x\). Следовательно, по теореме Пифагора \[BC^2+AC^2=AB^2\quad\Rightarrow\quad x^2+(5x)^2=13^2\quad\Rightarrow\quad x^2=\dfrac{13}2\] Из \(\triangle AHC\): \[\cos \angle A=\dfrac{AH}{AC}\] Из \(\triangle ABC\): \[\cos \angle A=\dfrac{AC}{AB}\] Следовательно: \[\dfrac{AH}{AC}=\dfrac{AC}{AB}\quad\Rightarrow\quad AH=\dfrac{AC^2}{AB}=\dfrac{(5x)^2}{13}=\dfrac{25}2=12,5\]
В треугольнике \(ABC\) угол \(C=90^\circ\), \(CH\) – высота, \(AB=26\), \(\mathrm{tg}\,\angle B=5\). Найдите \(AH\).
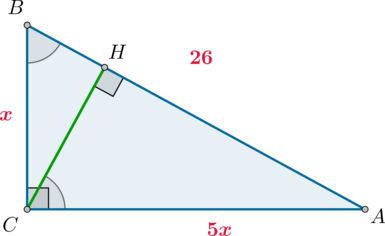
По определению из \(\triangle ABC\): \[\dfrac{AC}{BC}=\mathrm{tg}\,\angle B=\dfrac 51\] Следовательно, можно принять \(AC=5x\), \(BC=x\). Тогда по теореме Пифагора \(x^2+(5x)^2=26^2\), откуда \(x=\sqrt{26}\).
Тогда \[\sin\angle B=\dfrac{AC}{AB}=\dfrac5{\sqrt{26}}\] По свойству прямоугольного треугольника \(\angle B=\angle HCA\). Следовательно, из \(\triangle HCA\): \[\dfrac5{\sqrt{26}}=\sin \angle HCA=\dfrac{AH}{AC}\quad\Rightarrow\quad
AH=25\]
В треугольнике \(ABC\) угол \(C=90^\circ\), \(AB=17\), \(\mathrm{tg}\,\angle A=0,25\). Найдите высоту \(CH\).
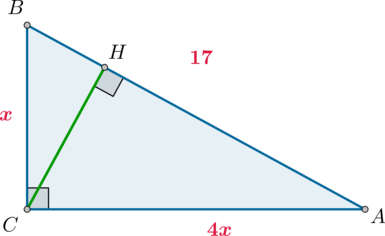
По определению из \(\triangle ABC\): \[\dfrac{BC}{AC}=\mathrm{tg}\,\angle A=\dfrac 14\] Следовательно, можно принять \(AC=4x\), \(BC=x\). Тогда по теореме Пифагора \(x^2+(4x)^2=17^2\), откуда \(x=\sqrt{17}\).
Так как площадь прямоугольного треугольника \(ABC\), с одной стороны, равна \(0,5CH\cdot AB\), а с другой стороны, равна \(0,5BC\cdot AC\), то \[CH\cdot AB=BC\cdot AC\quad\Rightarrow\quad CH=\dfrac{4x^2}{AB}=4\]



