Геометрия на плоскости (планиметрия). Часть II (страница 5)
Готовиться с нами - ЛЕГКО!

В треугольнике \(ABC\): высота \(CH\) равна \(2\sqrt6\), косинус угла \(A\) равен \(0,2\). Найдите \(AC\).
Рассмотрим \(\triangle ABC\):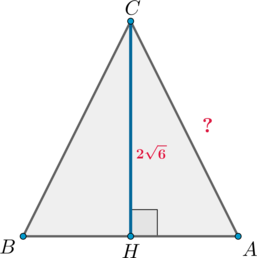
Так как косинус угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе, то в \(\triangle AHC:\) \[\cos A=\dfrac{AH}{AC}=\dfrac15\] Следовательно, можно принять \(AH=x\), \(AC=5x\). Тогда по теореме Пифагора из этого же треугольника: \[AC^2=AH^2+CH^2 \quad\Rightarrow\quad 25x^2=x^2+24 \quad\Leftrightarrow\quad x=\pm 1.\] Так как длина отрезка – неотрицательное число, то \(x=1\) и \(AC=5x=5.\)
В прямоугольном треугольнике \(CAT\) из вершины \(C\) прямого угла опущена высота \(CH\). Известно, что \(TH=12, CH=5\). Найдите \(13\sin \angle A\).
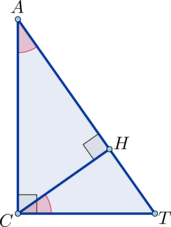
По свойству прямоугольного треугольника и высоты, опущенной из его прямого угла, \(\triangle CHT\sim \triangle CAT\). Значит, \(\angle HCT=\angle A\). Поэтому будем искать \(\sin \angle HCT\).
Из треугольника \(HCT\): \[\sin \angle HCT=\dfrac{TH}{TC}\]
По теореме Пифагора из этого же треугольника мы можем найти \(TC\):
\[TC=\sqrt{TH^2+CH^2}=\sqrt{12^2+5^2}=13\]
Следовательно, \[\sin \angle A=\sin\angle HCT=\dfrac{12}{13} \quad \Rightarrow \quad 13\sin \angle A=12.\]
В четырёхугольнике \(ABCD\): \(AD = 5\), \(AD\parallel BC\), \(BD\) перпендикулярна к \(AD\), \(\sin{\angle A} = \cos{\angle A}\), \(\sin{\angle C} = \dfrac{5}{\sqrt{34}}\). Найдите \(BC\).
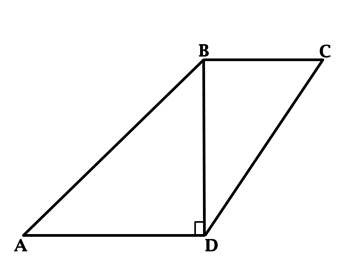
Треугольник \(ABD\) – прямоугольный, тогда \(\angle A\) – острый. В силу основного тригонометрического тождества (для любого угла \(\alpha\) выполнено \(\sin^2{\alpha} + \cos^2{\alpha} = 1\)) из равенства \(\sin{\angle A} = \cos{\angle A}\) получаем, что \[\sin{\angle A} = \pm \dfrac{1}{\sqrt{2}},\] но \(\angle A\) – острый, тогда \[\sin{\angle A} = \dfrac{1}{\sqrt{2}}\] и, значит, \(\angle A = 45^{\circ}\).
\(\angle ABD = 90^{\circ} - \angle A = 45^{\circ} = \angle A\), тогда треугольник \(ABD\) – равнобедренный и \(BD = AD = 5\).
\(AD || BC\), \(BD\) перпендикулярна к \(AD\), тогда \(BD\) перпендикулярна и к \(BC\).
Так как синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, то \[\dfrac{5}{\sqrt{34}} = \dfrac{5}{CD} \qquad\Rightarrow\qquad CD = \sqrt{34}.\]
По теореме Пифагора \(BC^2 = CD^2 - BD^2 = 34 - 25 = 9 = 3^2\), тогда \(BC = 3\).
Дан прямоугольный \(\triangle CAT\) с острыми углами \(A\) и \(T\). Точка \(H\) – такая точка на стороне \(AT\), что \(\cos \angle ACH=\cos \angle ATC=0,2\). Найдите \(HT\), если известно, что \(AT=2,5\).

Т.к. косинусы углов \(ACH\) и \(ATC\) равны, то равны и эти углы (т.к. это углы треугольников). Следовательно, \(\triangle ACH\sim \triangle CAT\) по двум углам (\(\angle ACH=\angle ATC, \ \angle A\) – общий). Следовательно, \(\angle AHC=\angle ACT=90^\circ\), то есть \(\triangle ACH\) тоже прямоугольный.
По свойству прямоугольного треугольника и высоты, опущенной из вершины его прямого угла, \(\triangle CHT\sim \triangle CAT\).
По определению косинуса \(\cos \angle CTH=\dfrac{HT}{CT}\). Следовательно, необходимо найти \(CT\).
Из треугольника \(CAT\): \[\cos \angle ATC=\dfrac{CT}{AT}=0,2 \quad \Rightarrow \quad CT=AT\cdot 0,2=2,5\cdot 0,2=0,5\]
Следовательно, \[HT=CT\cdot \cos \angle CTH=0,5\cdot 0,2=0,1.\]
В треугольнике \(ABC\): \(\angle A = 90^{\circ}\), \(\mathrm{ctg}\, \angle B = 0,6\). Площадь треугольника \(ABC\) равна \(7,5\). Найдите \(AB + AC\).
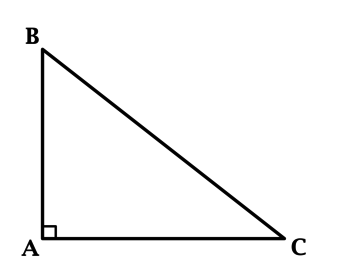
\[0,6 = \mathrm{ctg}\, \angle B = \dfrac{AB}{AC}.\]
Площадь треугольника \(ABC\) равна \(7,5\), тогда \(7,5 = 0,5\cdot AB\cdot AC\).
Таким образом, \[\dfrac{AB}{AC} = 0,6,\qquad AB\cdot AC = 15.\] Перемножая равенства, получим \(AB^2 = 9\), тогда \(AB = 3\), \(AC = 5\), значит, \(AB + AC = 8\).
В прямоугольнике \(ABCD\) известно, что \(BC:AB = 2:1\), \(AC\) – диагональ. Найдите отношение косинуса угла \(CAD\) к косинусу угла \(ACD\).
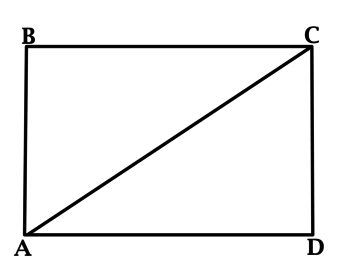
По определению косинуса и синуса острого угла в прямоугольном треугольнике получаем, что \(\cos{\angle ACD} = \sin{\angle CAD}\), тогда \[\dfrac{\cos{\angle CAD}}{\cos{\angle ACD}} = \dfrac{\cos{\angle CAD}}{\sin{\angle CAD}} = \mathrm{ctg}\, \angle CAD = \dfrac{AD}{CD} = \dfrac{BC}{AB} = 2.\]


