Окружность: важные теоремы, связанные с углами
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Радиус, проведенный в точку касания, перпендикулярен касательной;
\(\blacktriangleright\) Угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними; \[\alpha = \dfrac{1}{2}\buildrel\smile\over{AB}\]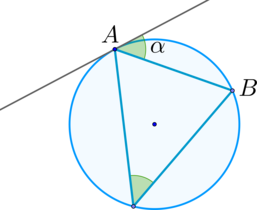
\(\blacktriangleright\) Угол между двумя секущими, проведенными из одной точки вне окружности, равен полуразности дуг, заключенных между ними; \[\alpha =
\dfrac{1}{2}\left(\buildrel\smile\over{AB}-\buildrel\smile\over{CD}\right)\]
\(\blacktriangleright\) Угол между двумя хордами равен полусумме дуг, заключенных между ними; \[\alpha =
\dfrac{1}{2}\left(\buildrel\smile\over{AB}+\buildrel\smile\over{CD}\right)\]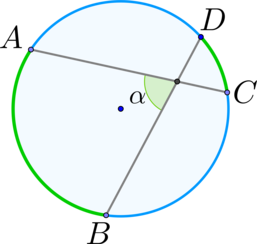
\(\blacktriangleright\) Прямая, проходящая через точку вне окружности и центр окружности, является биссектрисой угла, образованного касательными, проведенными из этой точки к окружности;
\(\blacktriangleright\) Если радиус делит хорду пополам, то он ей перпендикулярен;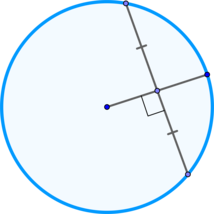
\(\blacktriangleright\) Вписанный угол, опирающийся на диаметр, равен \(90^\circ\);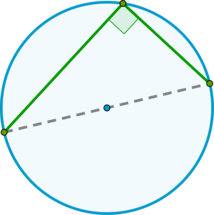
\(\blacktriangleright\) Дуги (меньшие полуокружности),отсекаемые равными хордами, равны между собой.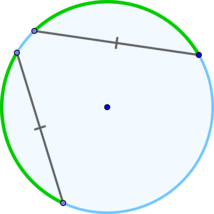
\(AC\) – диаметр окружности с центром в точке \(O\). Найдите \(\angle ABC\), если \(B\) лежит на окружности. Ответ дайте в градусах
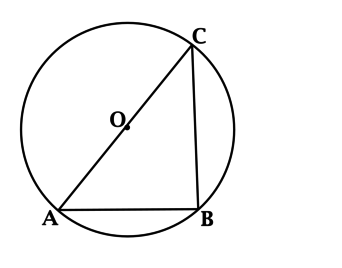
\(\angle ABC\) – вписанный. Вписанный угол в два раза меньше градусной меры дуги, на которую он опирается.
Градусная мера дуги есть градусная мера центрального угла, который на неё опирается, тогда градусная мера дуги \(AC\) равна \(180^{\circ}\) и \(\angle ABC = 90^{\circ}\).
\(AB\) – диаметр окружности с центром в точке \(O\), \(CD\) – хорда, пересекающая \(AB\) в точке \(E\), причём \(CE = ED\). Найдите \(\angle CEB\). Ответ дайте в градусах.
Хорда, делящаяся диаметром пополам, перпендикулярна ему. Покажем это:
Построим радиусы \(OC\) и \(OD\).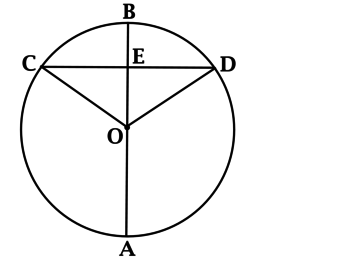
Треугольники \(COE\) и \(DOE\) равны по трём сторонам, тогда \(\angle CEO = \angle DEO\), но \(\angle CEO + \angle DEO = 180^{\circ}\), откуда \(\angle CEO = 90^{\circ}\). \[\angle CEB = 180^{\circ} - \angle CEO = 90^{\circ}.\]
Хорды \(AB\) и \(CD\) равны. Найдите разность градусных мер дуг \(AB\) и \(CD\), которые меньше полуокружности. Ответ дайте в градусах.
Равные хорды стягивают равные дуги. Покажем это:
Построим радиусы \(OA\), \(OB\), \(OC\), \(OD\)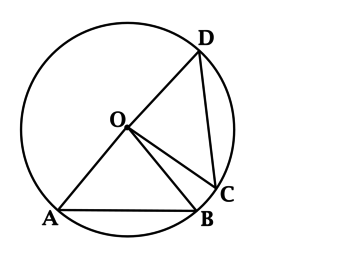
Треугольники \(AOB\) и \(COD\) равны по трём сторонам, тогда \(\angle AOB = \angle COD\) и, значит, дуга \(AB\) (которая меньше полуокружности) равна дуге \(CD\) (которая меньше полуокружности). Тогда разность градусных мер этих дуг равна \(0^{\circ}\).
Найдите угол между двумя секущими, проведенными к окружности из точки \(O\) вне окружности, если дуги, заключенные между этими секущими, равны \(103^\circ\) и \(47^\circ\). Ответ дайте в градусах.
Рассмотрим картинку: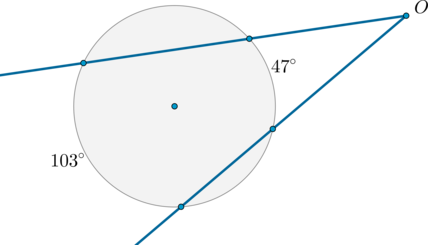
Т.к. угол, образованный двумя такими секущими, равен полуразности дуг, заключенных между ними, то
\[\angle O=\dfrac12\left(103^\circ-47^\circ\right)=28^\circ.\]
Точки \(A\), \(B\), \(C\) и \(D\) угла \(AOB\) лежат на окружности. Дуга \(AB\), заключённая внутри этого угла, равна \(65^{\circ}\), а дуга \(CD\), заключённая внутри этого угла, равна \(22^{\circ}\). Найдите величину угла \(AOB\). Ответ дайте в градусах.
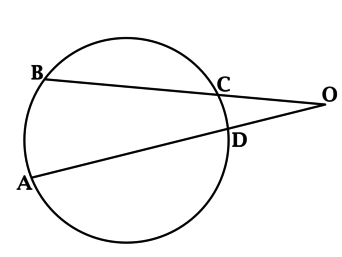
\(\angle AOB\) равен полуразности дуг \(AB\) и \(CD\), заключённых внутри него, тогда \[\angle BOD = 0,5(\smile AB - \smile CD) = 0,5(65^{\circ} - 22^{\circ}) = 21,5^{\circ}.\]
Из точки \(O\) вне окружности проведены две прямые, пересекающие окружность. Большая дуга, образованная этими прямыми, равна \(44^\circ\), а угол между прямыми равен \(15^\circ\). Найдите другую дугу, образованную этими прямыми. Ответ дайте в градусах.
Рассмотрим картинку: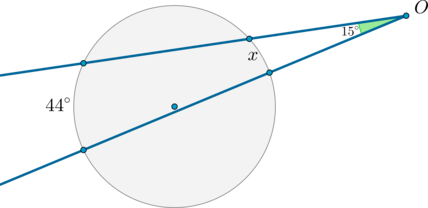
Т.к. угол, образованный двумя такими прямыми-секущими, равен полуразности дуг, заключенных между ними, то
\[\angle O=15^\circ=\dfrac12\left(44^\circ-x\right)\quad \Rightarrow \quad x=14^\circ\]
Прямая \(b\) касается окружности в точке \(B\) и образует с хордой \(AB\) угол, равный \(55^{\circ}\). Найдите градусную меру дуги \(AB\), которая меньше полуокружности. Ответ дайте в градусах.
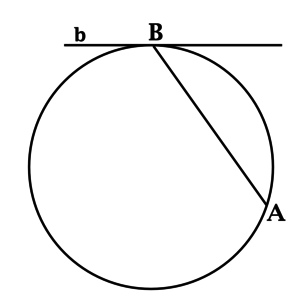
Угол между касательной и хордой равен половине градусной меры дуги окружности, заключённой внутри него, следовательно градусная мера искомой дуги равна \(2\cdot 55^{\circ} = 110^{\circ}\).
Планиметрические задачи на применение теоремы об углах в окружности встречаются в ЕГЭ из года в год. Как правило, данная тема подробно рассматривается в 8—9 классе. В связи с этим у выпускников часто возникает потребность в повторении основных теорем про углы в окружности. Поскольку подобные задачи часто включаются и в базовый, и в профильный уровень экзамена, знать алгоритм их выполнения должны абсолютно все учащиеся, независимо от уровня подготовки. Освежив в памяти базовую теорию и практические примеры, в которых применяется теорема о внешнем угле окружности, старшеклассники смогут рассчитывать на получение достаточно высоких баллов по итогам сдачи ЕГЭ.
Готовьтесь к прохождению аттестационного испытания вместе с образовательным порталом «Школково»!
Часто процесс поиска нужного источника, в котором представлена вся необходимая информация, отнимает достаточно большое количество времени. Учебник далеко не всегда есть под рукой. А найти нужные формулы нередко оказывается проблематично даже в Интернете.
Отточить навыки и улучшить собственные знания в таком непростом разделе геометрии, как планиметрия, а также по задачам по теме «Центральные и вписанные углы окружности», вам поможет наш образовательный портал. «Школково» предлагает учащимся и их преподавателям по-новому выстроить процесс подготовки к сдаче единого государственного экзамена.
Чтобы задачи ЕГЭ на применение теоремы о дугах окружности и углах давались легко, мы рекомендуем прежде всего повторить определения и основные правила. Сделать это вы можете, посетив раздел «Теоретическая справка». Здесь наши специалисты изложили материал, подготовленный специально для старшеклассников с различным уровнем подготовки. А для закрепления полученных знаний мы предлагаем выполнить соответствующие упражнения. Богатая подборка задач представлена в разделе «Каталог». Мы сгруппировали как простые, так и более сложные задания и для каждого из них прописали алгоритм решения и правильный ответ. База задач в соответствующем разделе постоянно дополняется и обновляется.
Выполнять упражнения на образовательном портале «Школково» могут все старшеклассники независимо от того, в каком регионе нашей страны они проживают. При необходимости любое задание может быть сохранено в разделе «Избранное». Это позволит выпускнику в дальнейшем быстро его найти и, к примеру, обсудить алгоритм решения со школьным преподавателем или репетитором.



