Окружность: важные теоремы, связанные с длинами отрезков
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Если радиус перпендикулярен хорде, то он делит ее пополам;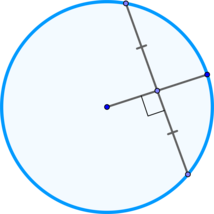
\(\blacktriangleright\) Если вписанный угол – прямой, то он опирается на диаметр;
\(\blacktriangleright\) Произведения отрезков хорд равны; \[\large{AO
\cdot OC=BO\cdot OD}\]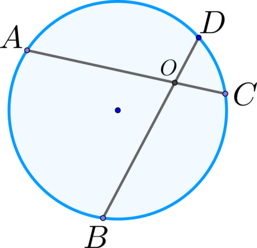
\(\blacktriangleright\) Квадрат касательной равен произведению секущей на ее внешнюю часть; \[\large{OA^2=OB\cdot OC}\]
\(\blacktriangleright\) Произведения двух секущих, проведенных из одной точки вне окружности, на их внешние части одинаковы;\[\large{
OA\cdot OC=OB\cdot OD}\]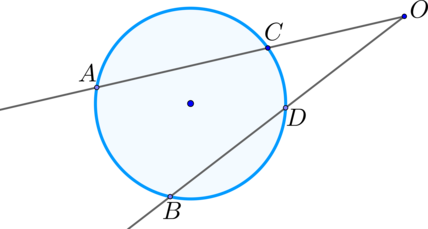
\(\blacktriangleright\) Отрезки касательных, проведенных из одной точки, равны;\[\large{OA=OB}\]
\(\blacktriangleright\) Если хорды отсекают от окружности равные дуги (меньшие полуокружности), то такие хорды равны.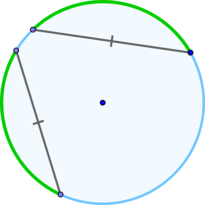
Хорды \(AB\) и \(CD\) пересекаются в точке \(P\), причём \(AP = 6\), \(PB = 4\), \(PC = 3\). Найдите \(PD\).
Произведение отрезков одной из пересекающихся хорд равно произведению отрезков другой. Покажем это:
Соединим \(AC\) и \(BD\)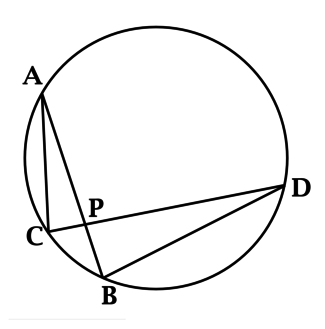
Рассмотрим треугольники \(APC\) и \(PBD\):
\(\angle APC = \angle BPD\), как вертикальные,
\(\angle ACD\) и \(\angle ABD\) – вписанные, опирающиеся на одну дугу, следовательно, \(\angle ACD = \angle ABD\).
Таким образом, треугольники \(APC\) и \(PBD\) – подобны по двум углам. Из их подобия следует, что \[\dfrac{CP}{PB} = \dfrac{AP}{PD}\] (в подобных треугольниках против равных углов лежат пропорциональные стороны), откуда можно получить \(CP \cdot PD = AP \cdot PB\).
В данной задаче имеем: \(3 \cdot PD = 6 \cdot 4\), откуда \(PD = 8\).
Из точки \(A\) вне окружности проведена касательная \(AB\) и секущая \(AD\), как показано на картинке.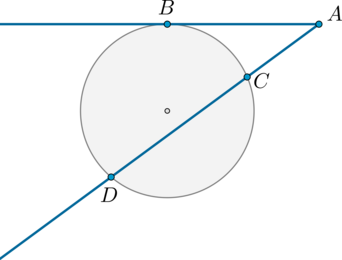
Найдите длину отрезка \(CD\), если \(AC=5\), а длина отрезка касательной равна \(10\).
Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то \[AB^2=AC\cdot AD=AC\cdot (AC+CD),\] откуда \[10^2=5\cdot (5+CD) \quad \Rightarrow \quad CD=15.\]
Из точки \(A\) вне окружности проведена касательная \(AB\) и секущая \(AD\), как показано на картинке.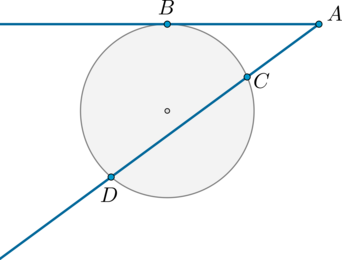
Найдите длину отрезка \(AC\), если \(CD=14\), а \(AB=6\sqrt2\).
Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то \[AB^2=AC\cdot AD=AC\cdot (AC+CD),\] откуда \[(6\sqrt2)^2=AC\cdot (AC+14) \quad \Rightarrow \quad AC^2+14AC-72=0 \quad \Rightarrow \quad AC=4 \text{ или } AC=-18\]
Т.к. длина отрезка – неотрицательное число, то \(AC=4\).
В треугольнике \(ABC\): \(\angle C = 90^{\circ}\), \(AB = 10\), \(CO\) – медиана. Найдите длину \(CO\).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине. Покажем это:
Опишем около треугольника \(ABC\) окружность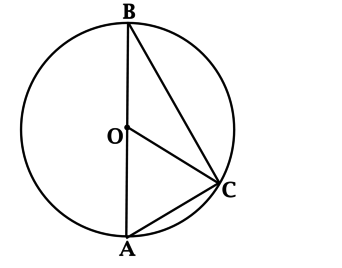
\(\angle ACB = 90^{\circ}\) – вписанный, тогда он равен половине градусной меры дуги, на которую опирается, следовательно, градусная мера дуги \(AB\) равна \(180^{\circ}\), а значит, \(AB\) – диаметр и \(O\) – центр описанной около \(ABC\) окружности, тогда \(AO = OC\) как радиусы. \[OC = AO = 0,5 \cdot AB = 5.\]
Дана окружность с центром в точке \(O\) и радиусом \(R\). Её хорды \(AB\) и \(CD\) пересекаются в точке \(K\). Известно, что \(AK = KB\), \(CK = AB\). Найдите \(KD : CD\).
Так как \(AB\) и \(CD\) – пересекающиеся в точке \(K\) хорды, то \[AK\cdot KB = CK\cdot KD\] 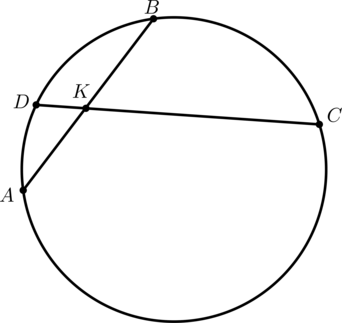
Тогда \(AK^2 = 2AK\cdot KD\), откуда \[KD = 0,5AK = 0,25 AB = 0,25 CK,\] следовательно, \(CK = 4KD\), тогда \(CD = CK + KD = 5KD\), откуда \(KD : CD = 0,2\).
Луч \(PA\) касается окружности в точке \(A\), а луч \(PC\) пересекает эту окружность в точках \(B\) и \(C\). При этом \(PA = 4\), \(PC = 8\). Найдите \(PB\).
Квадрат отрезка касательной равен произведению отрезков секущей: \(AP^2 = PB \cdot PC\). Покажем это:
Соединим \(AB\) и \(AC\)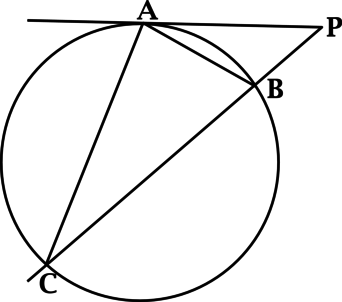
Рассмотрим треугольники \(APB\) и \(APC\):
\(\angle APC\) – общий,
Так как угол между касательной и хордой равен половине градусной меры дуги окружности, заключённой внутри него, то \(\angle PAB = 0,5\cdot \smile AB = \angle ACB\).
Таким образом, треугольники \(APC\) и \(APB\) – подобны по двум углам. Из их подобия следует, что \[\dfrac{AP}{PC} = \dfrac{PB}{AP}\] (в подобных треугольниках против равных углов лежат пропорциональные стороны), откуда можно получить \(AP^2 = PB \cdot PC\).
В данной задаче имеем: \(16 = PB \cdot 8\), откуда \(PB = 2\).
Точки \(B\), \(C\), \(D\) и \(E\) угла \(CAE\) лежат на окружности, причём точка \(B\) лежит на \(AC\), \(AB = 3\), \(AC = 6\), \(AD = 2\). Найдите \(DE\).
Произведение отрезков секущих равны: \(AB \cdot AC = AD \cdot AE\). Покажем это:
Построим \(AF\) – касательную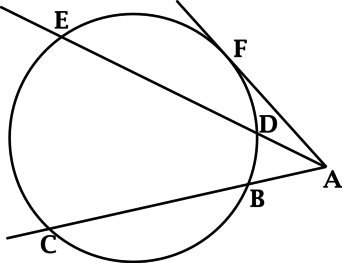
Так как квадрат отрезка касательной равен произведению отрезков секущей, то \(AB \cdot AC = AF^2 = AD \cdot AE\).
В данной задаче имеем: \(18 = 2 \cdot AE\), откуда \(AE = 9\), тогда \(DE = AE - AD = 9 - 2 = 7\).
Если старшеклассник готовится к сдаче ЕГЭ по математике базового уровня и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит повторить все теоремы, связанные с длинами отрезков.
Как показывает практика, подобные планиметрические задания включаются в аттестационное испытание каждый год. Это означает, что справляться с задачами ЕГЭ на применение теорем, связанных с длинами отрезков, должны все выпускники, независимо от уровня их подготовки.
Полезная информация
Для того чтобы решить задачи ЕГЭ с применением теорем, связанных с длинами отрезков, рекомендуется следовать определенного алгоритму. Сначала стоит выполнить чертеж. Затем нужно нанести на него все известные параметры исходя из условия задачи. После этого стоит вспомнить относящиеся к ним понятия и теоремы. Затем отразите на чертеже все соотношения между элементами, которые следуют из них логически. Сопоставив имеющиеся параметры, вы сможете найти правильный ответ.
Как подготовиться к экзамену?
Планиметрические задачи вызывают у вас сложность? Образовательный портал «Школково» поможет восполнить пробелы в знаниях. На нашем сайте учащиеся смогут найти и повторить материал, который вызывает затруднения. Наши специалисты собрали и изложили всю теоретическую информацию в максимально доступной и понятной форме.
Все упражнения на сайте, например, задачи на тему «Окружность в ЕГЭ», содержат подробный алгоритм решения и правильный ответ. Выполнять простые и более сложные задания школьники из Москвы и других городов могут в режиме онлайн. Любое задание в случае необходимости возможно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему для обсуждения с преподавателем или репетитором.



