Работа с внешними углами многоугольника с помощью тригонометрии
Готовиться с нами - ЛЕГКО!

Внешний угол многоугольника – угол, смежный с каким-нибудь внутренним углом многоугольника.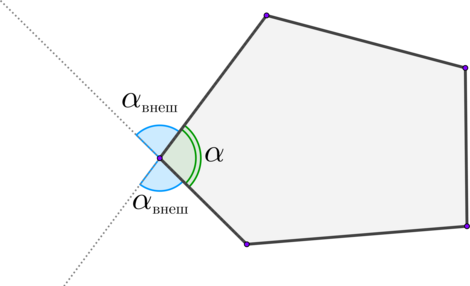
\[\large{\begin{aligned} &\sin \alpha_{\text{внеш}}=\sin \alpha \qquad \qquad \qquad \cos \alpha_{\text{внеш}}=-\cos \alpha\\ &\\ &\mathrm{tg}\, \alpha_{\text{внеш}}=-\, \mathrm{tg}\,\alpha \qquad \qquad \qquad \, \mathrm{ctg}\, \alpha_{\text{внеш}}= -\, \mathrm{ctg}\,\alpha \end{aligned}}\]
Замечание: Синус и острого, и тупого угла – положительное число. Косинус, тангенс и котангенс острого угла – положительное число, а тупого угла – отрицательное число.
(острый угол: \(0^\circ<\alpha<90^\circ\), тупой угол: \(90^\circ<\alpha<180^\circ\))
Дан выпуклый четырехугольник \(GEOM\), причем \(\angle G+\angle E+\angle O=330^\circ\). Найдите синус внешнего угла при вершине \(M\).
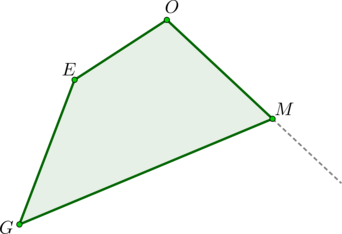
Т.к. сумма углов любого выпуклого четырехугольника равна \(360^\circ\), то \(\angle M=360^\circ - 330^\circ =30^\circ\). Следовательно, \(\sin \angle M=\sin 30^\circ =0,5\). Т.к. синусы смежных углов равны, то \(\sin M_{\text{внеш}}=0,5\).
Дан треугольник \(ABC\), причем \(\sin (\angle A+\angle B)=0,67\). Найдите синус угла \(ACB\).

Т.к. в треугольнике внешний угол при вершине \(C\) равен сумме углов \(A\) и \(B\), то и \(\sin \angle C_{\text{внеш}}=\sin (\angle A+\angle
B)=0,67\).
Т.к. синусы смежных углов равны, то \(\sin \angle C=\sin \angle
C_{\text{внеш}}=0,67\).
В треугольнике \(ABC\): \(\angle B < 90^{\circ}\), \(\sin {\angle ABC} = 0,8\). Найдите косинус внешнего угла при вершине \(B\).
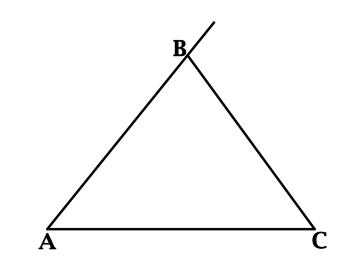
Синусы смежных углов равны: \(\sin{(180^{\circ} - \alpha)} = \sin{\alpha}\), тогда синус внешнего угла при вершине \(B\) равен \(0,8\).
Используя основное тригонометрическое тождество (\(\sin^2{\alpha} + \cos^2{\alpha} = 1\)), находим, что косинус внешнего угла при вершине \(B\) равен \(\pm 0,6\).
Так как \(\angle ABC < 90^{\circ}\), то внешний угол при вершине \(B\) – тупой, следовательно, его косинус отрицателен. Косинус внешнего угла при вершине \(B\) равен \(-0,6\).
В треугольнике \(ABC\) известно, что \(\cos (\angle B+\angle C)=0,33\). Найдите косинус угла \(A\).

Т.к. в треугольнике внешний угол при вершине \(A\) равен сумме углов \(B\) и \(C\), то \(\cos \angle A_{\text{внеш}}=\cos(\angle B+\angle
C)=0,33\).
Т.к. косинусы смежных углов отличаются только знаком, то \(\cos
\angle A=-\cos \angle A_{\text{внеш}}=-0,33\).
Дан выпуклый пятиугольник, причем сумма четырех его внутренних углов равна \(420^\circ\). Найдите квадрат косинуса внешнего угла при вершине оставшегося пятого угла.
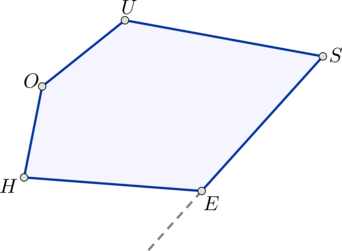
Т.к. сумма внутренних углов выпуклого \(n\)-угольника вычисляется по формуле \(180^\circ \cdot (n-2)\), то сумма внутренних углов нашего пятиугольника равна \(540^\circ\). Следовательно, если \(\angle
H+\angle O+\angle U+\angle S=420^\circ \quad \Rightarrow \quad
\angle E=540^\circ -420^\circ =120^\circ\).
Следовательно, \(\angle E_{\text{внеш}}=180^\circ -\angle
E=60^\circ\). Следовательно, \(\cos\angle E_{\text{внеш}}=\cos
^260^\circ =\dfrac14=0,25\).
В четырёхугольнике \(ABCD\) с тупыми углами \(C\) и \(D\) продолжение стороны \(AD\) за точку \(D\) и продолжение стороны \(BC\) за точку \(C\) пересеклись в точке \(E\) под прямым углом. При этом \(\sin{\angle DCE} = 0,6\). Найдите \(\sin{\angle ADC}\).
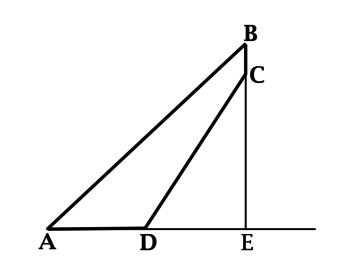
Из основного тригонометрического тождества с учётом того, что \(\angle DCE\) – острый, получаем: \(\cos{\angle DCE} = 0,8\).
Из определений синуса и косинуса острого угла в прямоугольном треугольнике получаем, что \(\sin{\angle EDC} = \cos{\angle DCE} = 0,8\).
Так как синусы смежных углов равны, то \(\sin{\angle ADC} = \sin{\angle EDC} = 0,8\).
В невыпуклом четырёхугольнике \(ABCD\) (\(\angle C > 180^\circ\)) сторону \(AD\) продолжили за точки \(A\) и \(D\), получив по одному внешнему углу при вершинах \(A\) и \(D\). \(\angle BAD = 2\cdot \angle CDA\). Найдите косинус внешнего угла при вершине \(A\), если косинус внешнего угла при вершине \(D\) получился \(-0,9\).
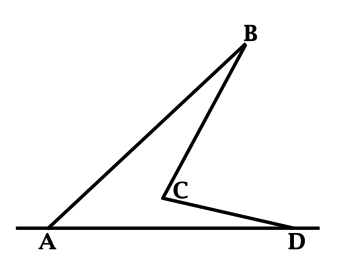
Косинусы смежных углов противоположны: \(\cos{(180^{\circ} - \alpha)} = -\cos{\alpha}\).
Косинус внешнего угла при вершине \(D\) равен \((-1)\cdot \cos{\angle CDA}\), откуда \(\cos{\angle CDA} = 0,9\).
\(\angle BAD = 2\cdot \angle CDA\), тогда \(\cos{\angle BAD} = 2\cos^2{\angle CDA} - 1 = 0,62\).
Так как косинус внешнего угла равен минус косинусу угла, смежного с ним, то косинус внешнего угла при вершине \(A\) равен \(-0,62\).
Задания, в которых школьникам необходимо найти внешние углы многоугольника, в ЕГЭ по математике традиционно встречаются из года в год. Правильно решать подобные задачи должны уметь выпускники, сдающие как базовый, так и профильный уровень аттестационного испытания. Школьники, которые освоили задания из раздела «Работа с внешними углами многоугольника», смогут справиться с ЕГЭ и рассчитывать на получение достойных баллов по итогам его прохождения.
Как подготовиться к экзамену?
Перед решением задач на нахождение внешних углов многоугольника в ЕГЭ стоит освежить в памяти определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике. Кроме того, для некоторых заданий могут потребоваться формулы основных тригонометрических тождеств.
Восполнить пробелы в знаниях, например, по теме «Вычисление синуса угла треугольника» и лучше усвоить информацию вам поможет образовательный проект «Школково». Для того чтобы выпускники могли успешно справляться с задачами на нахождение внешних углов треугольника в ЕГЭ, мы предоставляем возможность повторить определения и основные правила. Весь необходимый базовый материал вы найдете в разделе «Теоретическая справка». Наши специалисты подобрали соответствующую информацию.
Для закрепления теоретического материала мы предлагаем выполнить упражнения по теме «Работа с внешними углами многоугольника». Подборка простых и сложных заданий представлена в блоке «Каталог». Наши специалисты регулярно обновляют и дополняют упражнения.
Попрактиковаться в решении задач на нахождение внешних углов многоугольника, подобных тем, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.



