Использование различных формул площадей многоугольников
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Треугольник: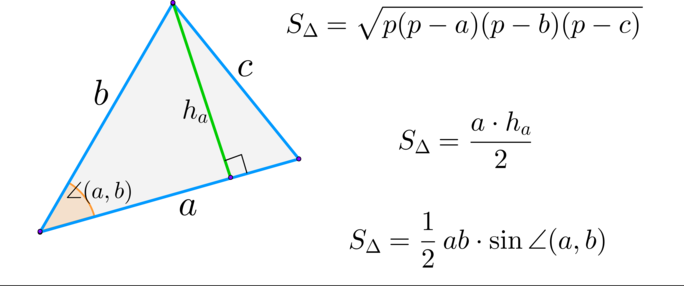
\(\blacktriangleright\) Произвольный выпуклый четырехугольник: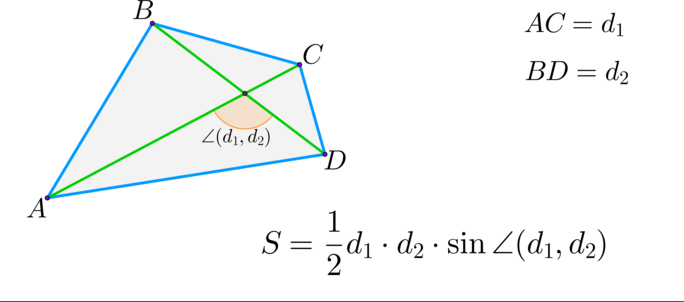
\(\blacktriangleright\) Параллелограмм: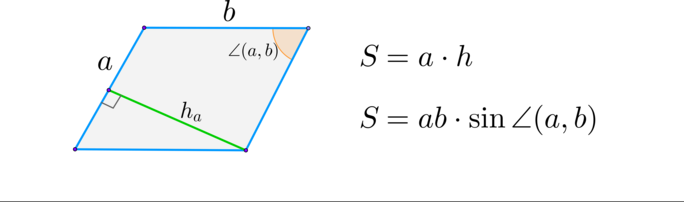
\(\blacktriangleright\) Ромб: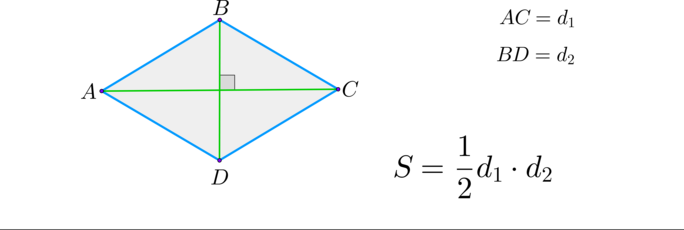
\(\blacktriangleright\) Прямоугольник:
\(\blacktriangleright\) Квадрат: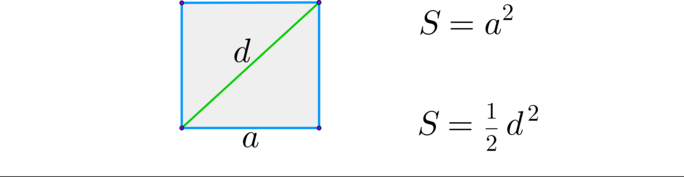
\(\blacktriangleright\) Трапеция:
В треугольнике \(ABC\): \(AD\) – высота, \(\cos{\angle DAC} = 0,7\), \(AC = 6\), \(BC = 9\). Найдите площадь треугольника \(ABC\).
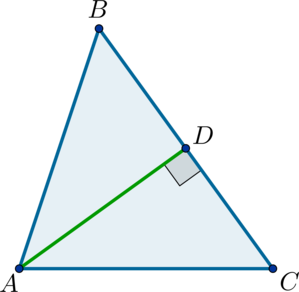
Так как \(AD\) перпендикулярна \(DC\), то \(\sin{\angle C} = \cos{\angle DAC} = 0,7\).
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,
тогда площадь треугольника \(ABC\) равна \(0,5\cdot 6 \cdot 9 \cdot 0,7
= 18,9\).
Периметр треугольника \(ABC\) равен \(250\), одна из его сторон равна \(120\), ещё одна сторона равна \(17\). Найдите его площадь.

Третья сторона треугольника равна \(250 - 120 - 17 = 113\).
По формуле Герона \(S_{\triangle ABC} = \sqrt{p(p - AB)(p - BC)(p -
AC)}\), где \(p\) – полупериметр треугольника \(ABC\).
Для данного треугольника
\(S_{\triangle ABC} = \sqrt{125\cdot (125 - 120)\cdot (125 - 17)\cdot (125 - 113)} = \sqrt{125\cdot 5 \cdot 12 \cdot 108} =\)
\(= 25\sqrt{12\cdot 108} = 100\sqrt{3\cdot 27} = 900.\)
Найдите высоту треугольника, проведенную к стороне длиной \(8\), если высота, проведенная к стороне длиной \(6\), равна \(4\).
Т.к. площадь треугольника равна полупроизведению высоты и стороны, к которой эта высота проведена, то с одной стороны площадь равна \[S=\dfrac12\cdot 6\cdot 4,\]
а с другой \[S=\dfrac12\cdot 8\cdot h,\]
где \(h\) – высота, которую нужно найти. Таким образом, получаем следующее равенство:
\[\dfrac12\cdot 6\cdot 4=\dfrac12\cdot 8\cdot h \quad \Leftrightarrow \quad h=3.\]
В треугольнике \(ABC\): \(AC = 4\), \(AB = 6\), \(\cos{\angle BAC} = \dfrac{\sqrt{15}}{4}\). Найдите площадь треугольника \(ABC\).

Из основного тригонометрического тождества:
\(\sin^2\angle BAC = 1 - \dfrac{15}{16}\), тогда \(\sin\angle BAC = \pm
0,25\). Так как \(\angle BAC \in (0^{\circ}; 180^{\circ})\), то \(\sin\angle BAC = 0,25\).
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,
тогда площадь треугольника \(ABC\) равна \(0,5\cdot 4 \cdot 6 \cdot
0,25 = 3\).
В прямоугольном треугольнике гипотенуза равна \(\sqrt[4]3\), а один из углов равен \(30^\circ\). Найдите площадь этого треугольника.
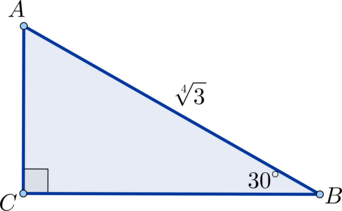
Т.к. катет, лежащий против угла в \(30^\circ\), равен половине гипотенузы, то \(AC=0,5\cdot AB=0,5\cdot \sqrt[4]3\).
Т.к. \(\angle A=90^\circ -\angle B=60^\circ\), то площадь равна \[S=\dfrac12\cdot AC\cdot AB\cdot \sin 60^\circ=\dfrac12\cdot 0,5\cdot \sqrt[4]3\cdot \sqrt[4]3\cdot \dfrac{\sqrt3}2=\dfrac38=0,375.\]
В ромбе \(ABCD\): \(O\) – точка пересечения диагоналей, \(BD = 8\), \(\mathrm{tg}\, \angle BDC = 3\). Найдите площадь ромба \(ABCD\).
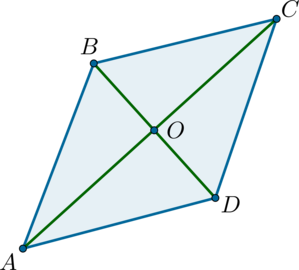
В ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, тогда \(OD = 4\), \(\dfrac{CO}{OD} = \mathrm{tg}\, \angle BDC = 3\), откуда \(CO = 12\), следовательно, \(AC = 24\).
Площадь ромба равна половине произведения его диагоналей, тогда \[S_{ABCD} = 0,5\cdot 8\cdot 24 = 96.\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Найдите боковую сторону этого треугольника, если его площадь равна \(100\).

Пусть \(a\) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[\dfrac12\cdot a^2\cdot \sin30^\circ=S=100\quad\Rightarrow\quad
a^2=400\quad\Rightarrow\quad a=20\]
Подготовка выпускников к сдаче аттестационного испытания по математике, как правило, начинается с повторения базовых определений и формул, в том числе и тех, которые позволяют произвести вычисление площадей плоских фигур в ЕГЭ. Данный раздел геометрии изучается в средней школе. Неудивительно, что с необходимостью повторения основных формул для правильного нахождения площади любого многоугольника сталкиваются многие выпускники. Умея выполнять расчеты с их применением, учащиеся смогут рассчитывать на получение конкурентных баллов по итогам сдачи аттестационного испытания.
Готовьтесь вместе с образовательным порталом «Школково»
Занимаясь перед сдачей экзамена, многие учащиеся сталкиваются с проблемой поиска определений и формул, которые позволяют выполнить вычисление площади правильного многоугольника в ЕГЭ. Школьный учебник далеко не всегда оказывается под рукой в нужный момент.
Вместе с образовательным порталом «Школково» подготовка к экзамену будет легкой и эффективной. Здесь представлен весь необходимый материал, подобранный и изложенный нашими специалистами в максимально понятной форме. Какая именно формула для нахождения площади многоугольника потребуется при работе с треугольником, четырехугольником, параллелограммом, ромбом, прямоугольником, квадратом, трапецией? Всю эту информацию вы найдете в разделе «Теоретическая справка». Ознакомившись с ней, выпускники смогут восполнить пробелы в знаниях.
Чтобы научиться быстро находить правильный ответ, необходимо также попрактиковаться в решении задач на нахождение площади фигур. Большая подборка упражнений представлена в разделе «Каталог». Для каждой задачи на нахождение площади фигур, например, вычисление площади параллелограмма, наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень упражнений на сайте постоянно дополняется и обновляется.
Любое задание, например, на подобие площадей подобных треугольников, выпускники могут сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти интересующее упражнение, например, с целью обсуждения хода его решения с преподавателем.



