Задачи, решаемые методом площадей (страница 2)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.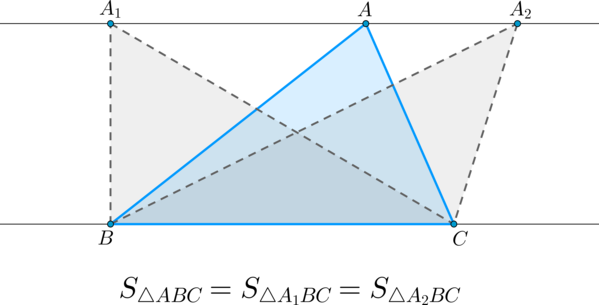
\(\blacktriangleright\) Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.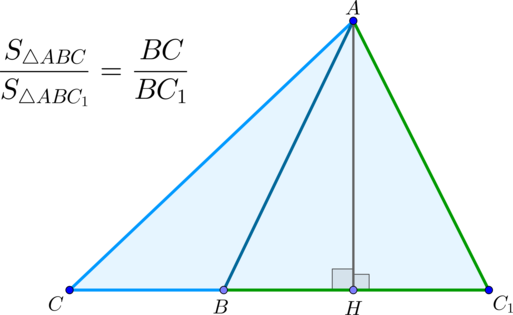
\(\blacktriangleright\) Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.
\(\blacktriangleright\) Следствие: медиана треугольника делит его на два треугольника, равных по площади.
\(\blacktriangleright\) Следствие: все три медианы треугольника делят его на шесть треугольников, равных по площади.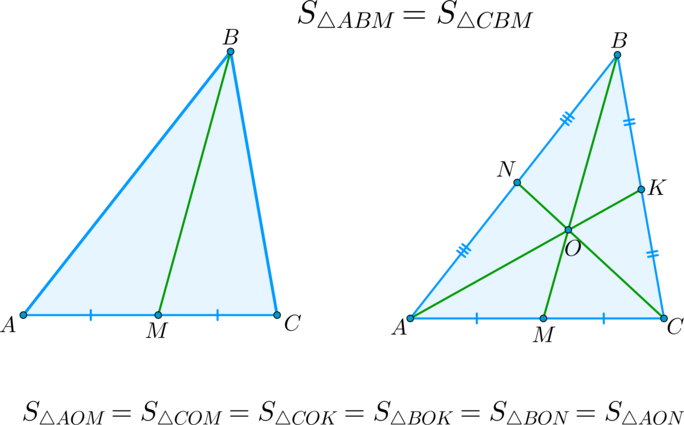
\(\blacktriangleright\) Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.
\(\blacktriangleright\) Следствие: биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.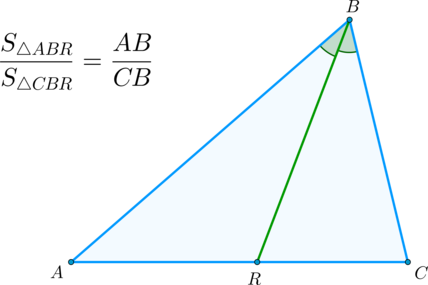
\(\blacktriangleright\) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.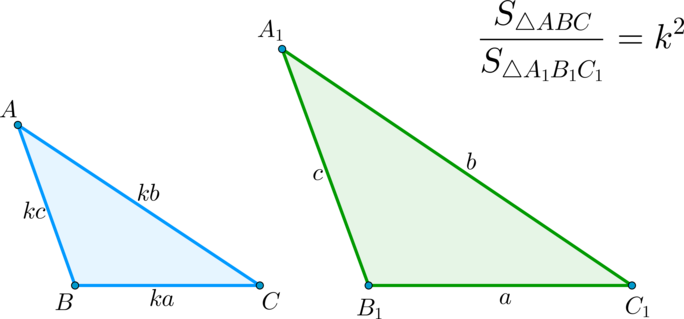
\(\blacktriangleright\) Следствие: все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.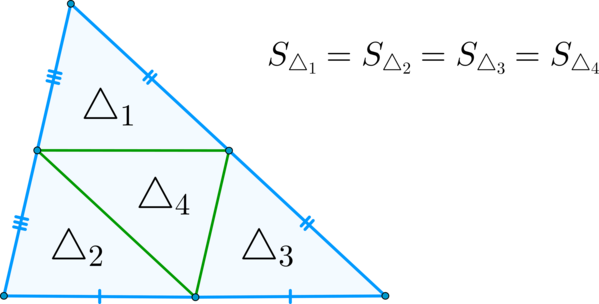
На стороне \(MN\) треугольника \(MNP\) отметили точки \(Q\), \(R\) и \(S\) так, что \(\angle MPQ = \angle QPR = \angle RPS = \angle SPN\).
а) Докажите, что если \(S_{\triangle NPR} = S_{\triangle RPM}\), то \(S_{\triangle PRS}\neq S_{\triangle NPS}\).
б) Найдите \(\dfrac{PS}{QP}\), если \(MP = a\), \(NP = b\), \(RP = c\).
а) Так как у треугольников \(NPR\) и \(RPM\) общая высота к основаниям \(NR\) и \(RM\) соответственно, то их площади относятся как их основания, то есть из \(S_{\triangle NPR} = S_{\triangle RPM}\) следует равенство \(NR = RM\).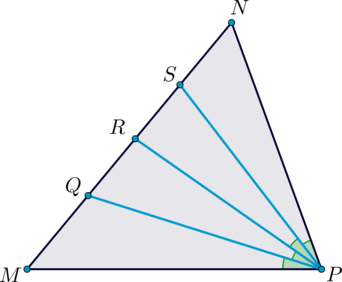
Тогда \(PR\) – медиана в треугольнике \(MNP\), которая является биссектрисой, откуда \(MP = NP\) и \(PR\) – высота.
Аналогично из равенства \(S_{\triangle PRS}\) и \(S_{\triangle NPS}\) следовало бы, что \(RP = NP\), но \(RP\perp MN\), а \(NP\) не совпадает с \(RP\), следовательно, \(NP > RP\) и \(S_{\triangle PRS}\neq S_{\triangle NPS}\).
б)
Первый способ.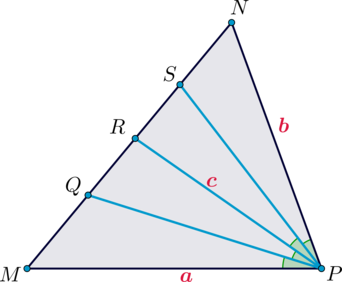
Обозначим \(\angle SPN = \alpha\), тогда \[S_{\triangle PNR} = 0,5\cdot bc\cdot\sin 2\alpha.\]
С другой стороны, \[S_{\triangle PNR} = S_{\triangle PNS} + S_{\triangle PSR} = 0,5\cdot b\cdot SP\cdot\sin\alpha + 0,5\cdot c\cdot SP\cdot\sin\alpha,\] тогда
\(0,5\cdot bc\cdot\sin 2\alpha=0,5\cdot b\cdot SP\cdot\sin\alpha + 0,5\cdot c\cdot SP\cdot\sin\alpha \quad \Leftrightarrow \quad 0,5\cdot 2\cos\alpha\sin\alpha\cdot bc = 0,5\sin\alpha\cdot SP(b+c)\quad \Leftrightarrow\)
\(\Leftrightarrow\quad 2\cos\alpha\cdot bc=SP(b+c) \quad
\Leftrightarrow \quad SP = \dfrac{2bc\cdot\cos\alpha}{b + c}.\)
так как \(a + c \ne 0\).
На самом деле здесь мы не ограничивая общности (т.е. к произвольному треугольнику можно применить те же рассуждения) выразили биссектрису треугольника через половину угла, из которого она выходит, и через стороны, заключающие этот угол.
Тогда аналогично \(PQ = \dfrac{2ac\cdot\cos\alpha}{a + c}\), откуда \[\dfrac{PS}{QP} = \dfrac{2bc\cdot\cos\alpha}{b + c}:\dfrac{2ac\cdot\cos\alpha}{a + c} = \dfrac{b(a + c)}{a(b + c)}.\]
Второй способ.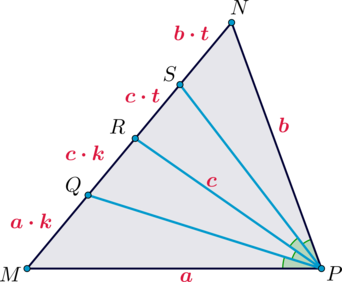
По свойству биссектрисы \(PS\) треугольника \(NPR\): \[\dfrac{PN}{PR}=\dfrac{NS}{RS}=\dfrac bc\] Следовательно, можно обозначить \(NS=b\cdot t\), \(RS=c\cdot t\), где \(t\) – некоторый коэффициент.
Аналогично для \(\triangle MPR\): \[\dfrac{MP}{RP}=\dfrac{MQ}{RQ}=\dfrac{a}{c}\] Следовательно, \(MQ=a\cdot k, RQ=c\cdot k\).
Теперь по этому же свойству для \(\triangle SPQ\) и биссектрисы \(PR\) имеем: \[\dfrac{PS}{PQ}=\dfrac{c\cdot t}{c\cdot k}=\dfrac tk\] Следовательно, необходимо найти отношение \(t:k\).
По этому же свойству для \(\triangle NPM\) и биссектрисы \(PR\): \[\dfrac{NP}{MP}=\dfrac{NR}{MR} \quad \Leftrightarrow \quad \dfrac ba=\dfrac{(b+c)\cdot t}{(a+c)\cdot k} \quad \Rightarrow \quad \dfrac tk=\dfrac{b(a+c)}{a(b+c)}=\dfrac{PS}{PQ}.\]
б) \(\dfrac{b(a + c)}{a(b + c)}\)
\(ABCD\) – параллелограмм, точки \(M\) и \(N\) лежат на сторонах \(AD\) и \(CD\) соответственно. \(AN\) пересекается с \(BM\) в точке \(P\), \(AN\) пересекается с \(CM\) в точке \(Q\), \(BN\) пересекается с \(CM\) в точке \(R\).
а) Докажите, что площади четырёхугольников \(AQCD\) и \(MBNQ\) равны.
б) Найдите \(\dfrac{PM}{RN}\), если \(\angle PRM = \angle RMN\) и около \(PRNM\) можно описать окружность.
а) Рассмотрим треугольник \(ABN\): его площадь равна \(0,5\cdot AB\cdot h_1\), где \(h_1\) – длина высоты, опущенной из точки \(D\) на \(AB\), следовательно, \(S_{ABN} = 0,5\cdot S_{ABCD}\).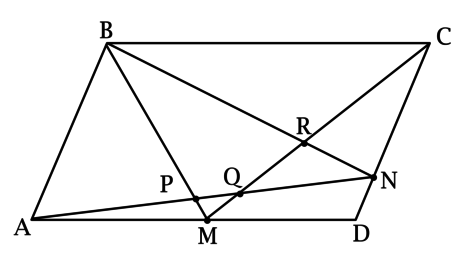
Рассмотрим треугольник \(BMC\): его площадь равна \(0,5\cdot BC\cdot h_2\), где \(h_2\) – длина высоты, опущенной из точки \(D\) на \(BC\), следовательно, \(S_{BMC} = 0,5\cdot S_{ABCD}\), тогда \[S_{ABM} + S_{MCD} = 0,5\cdot S_{ABCD}.\]
Таким образом, \(S_{ABN} = S_{ABM} + S_{MCD}\), откуда
\[(S_{ABP} + S_{PBN}) = (S_{ABP} + S_{APM}) + S_{MCD}\qquad\Leftrightarrow\qquad S_{PBN} = S_{APM} + S_{MCD}.\] тогда \[S_{PBN} + S_{PQM} = S_{APM} + S_{MCD} + S_{PQM},\] но \(S_{PBN} + S_{PQM} = S_{MBNQ}\), а \(S_{APM} + S_{MCD} + S_{PQM} = S_{AQCD}\).
В итоге \(S_{MBNQ} = S_{AQCD}\), что и требовалось доказать.
б)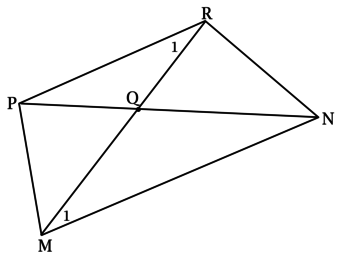
Так как \(\angle PRM = \angle RMN\), то внутренние накрест лежащие углы при прямых \(PR\), \(MN\) и секущей \(MR\) равны, следовательно, \(PR\parallel MN\), следовательно, \(PRNM\) либо параллелограмм, либо трапеция, а \(\angle MPR + \angle PMN = 180^\circ\), как сумма односторонних углов при параллельных прямых и секущей.
Так как около \(PRNM\) можно описать окружность, то \(\angle PMN + \angle PRN = 180^\circ\), откуда \(\angle PRN = \angle MPR\), то есть \(PRNM\) либо прямоугольник, либо равнобедренная трапеция. В любом случае \(PM = RN\), следовательно, \[\dfrac{PM}{RN} = 1.\]
б) \(1\).
Точки \(M, N, P\) лежат на сторонах \(AB, BC, CA\) треугольника \(ABC\), причем \(AM:AB=BN:BC=CP:CA=1:3\). При пересечении отрезков \(AN, BP, CM\) образуется треугольник \(A_1B_1C_1\), площадь которого равна \(1\). Найдите площадь треугольника \(ABC\).
1) Найдем часть, которую составляет \(S_{MAA_1}\) от \(S_{ABC}\). Для этого найдем, в каком отношении отрезок \(AN\) делится отрезком \(CM\). Проведем \(NN_1\parallel CM\). Тогда по теореме Фалеса \(N_1\) поделит отрезок \(BM\) в том же отношении, что \(N\) отрезок \(BC\).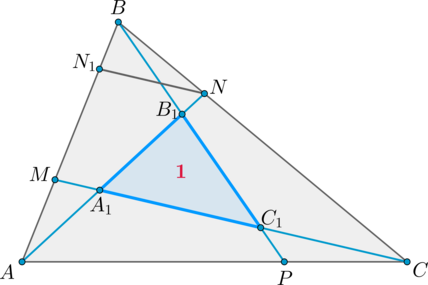
Следовательно, \(BN_1=\frac13BM=\frac13\cdot \frac23AB=\frac29AB\).
Также по условию \(AM=\frac13AB\). Тогда \[\dfrac{AA_1}{AN}=\dfrac{AM}{AN_1}=\dfrac{\frac13AB}{AB-\frac29AB}=\dfrac37\]
Следовательно, т.к. треугольники \(MAA_1\) и \(BAN\) имеют равный угол \(A\), то их площади относятся как произведения сторон, образующих этот угол:
\[\dfrac{S_{\triangle MAA_1}}{S_{\triangle BAN}}=\dfrac{AM\cdot AA_1}{AB\cdot AN}= \dfrac{\frac13AB\cdot \frac37AN}{AB\cdot AN}=\dfrac17\]
Таким образом, \(S_{\triangle MAA_1}=\frac17S_{\triangle BAN}\). Но в свою очередь \(\triangle BAN\) и \(\triangle ABC\) имеют одинаковую высоту, проведенную из вершины \(A\), значит, их площади относятся как основания, то есть \[\dfrac{S_{\triangle BAN}}{S_{\triangle ABC}}=\dfrac{BN}{BC}=\dfrac13\]
Таким образом, получаем \(S_{\triangle MAA_1}=\frac1{21}S_{\triangle ABC}\).
2) Аналогичным образом получаем, что \(S_{\triangle NBB_1}=\frac1{21}S_{\triangle ABC}\), \(S_{\triangle PCC_1}=\frac1{21}S_{\triangle ABC}\).
Итак,
\(1=S_{\triangle ABC}-S_{\triangle ABB_1}-S_{\triangle BCC_1}-S_{\triangle CAA_1}=\)
\(=S_{\triangle ABC}-\left(S_{\triangle BAN}-S_{\triangle NBB_1}\right)-\left(S_{\triangle CBP}-S_{\triangle PCC_1}\right)-\left(S_{\triangle CAM}-S_{\triangle MAA_1}\right)=\)
\(=S_{\triangle ABC}-3\cdot \left(\frac13S_{\triangle ABC}-\frac1{21}S_{\triangle ABC}\right)=\dfrac17S_{\triangle ABC}\)
Следовательно, \(S_{\triangle ABC}=7\).
На сторонах \(AC\) и \(BC\) треугольника \(ABC\) отмечены точки \(M\) и \(N\) соответственно так, что \(AM:MC=4:5\), \(BN:BC=0,25\). Отрезки \(BM\) и \(AN\) пересекаются в точке \(P\). Найдите площадь треугольника \(APM\), если площадь треугольника \(ABC\) равна \(63\).
1) Из условия задачи следует, что \(BN=\frac14BC\).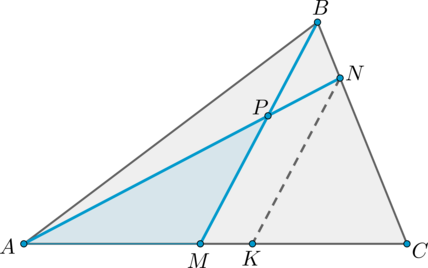
Обозначим \(S_{\triangle ABC}=S\). Тогда т.к. \(\triangle ABC\) и \(\triangle ABN\) имеют одинаковую высоту, опущенную из вершины \(A\), то \[\dfrac{S}{S_{\triangle ABN}}=\dfrac{BC}{BN}=4 \quad \Rightarrow\quad S_{\triangle ABN}=\dfrac14S\]
Аналогично рассуждая, получим
\[\dfrac{S}{S_{\triangle ABM}}=\dfrac{AC}{AM}=\dfrac94 \quad \Rightarrow \quad S_{\triangle ABM}=\dfrac49S\]
2) Найдем отношение \(AP:PN\), чтобы определить, какую часть составляет \(S_{\triangle ABP}\) от \(S_{\triangle ABN}\).
Проведем прямую \(NK\parallel BM\). Тогда по теореме Фалеса \[\dfrac{BN}{BC}=\dfrac{MK}{MC} \quad \Rightarrow \quad \dfrac14=\dfrac{MK}{MC} \quad \Rightarrow \quad MK=\dfrac14MC\]
Т.к. по условию \(AM:MC=4:5\), то можно принять \(AM=4x\), \(MC=5x\). Тогда \(MK=\frac54x\).
Опять же по теореме Фалеса \[\dfrac{AP}{PN}=\dfrac{AM}{MK} \quad \Rightarrow \quad \dfrac{AP}{PN}=\dfrac{4x}{\frac54x}=\dfrac{16}5 \quad \Rightarrow \quad AP=\dfrac{16}5PN\]
Значит, т.к. \(\triangle ABP\) и \(\triangle ABN\) имеют одинаковую высоту, опущенную из вершины \(B\), получаем
\[\dfrac{S_{\triangle ABN}}{S_{\triangle ABP}}=\dfrac{AN}{AP}=\dfrac{AP+PN}{AP}= \dfrac{21}{16}\]
Следовательно, \(S_{\triangle ABP}=\frac{16}{21}S_{\triangle ABN}=\frac4{21}S\).
Следовательно, \[S_{\triangle APM}=S_{\triangle ABM}-S_{\triangle ABP}=\dfrac49S-\dfrac4{21}S=\dfrac{16}{63}S \quad \Rightarrow \quad S_{\triangle APM}=16.\]


