Механическое равновесие
Готовиться с нами - ЛЕГКО!

Система, изображенная на рисунке, находится в равновесии. Стержень \(AC\) невесом и нить нерастяжима и невесома. К точкам \(C\) и \(B\) соответственно подвешены грузы \(m_1=0,1\) кг и \(m_2=0,2\) кг. Найти длину стержня АС, если \(AB=25\) см, углы \(\alpha=45^\circ\), \(\beta=15^\circ\), а масса перекинутого блока \(M=0,2\) кг. Ответ дайте в см и округлите до десятых.

“Основная волна 2020 Вариант 4”
Запишим правило моментов относительно точки А. В точке \(B\) действует только сила натяжения нити равная силе тяжести \(m_1g\), в точке \(C\) действует вниз сила натяжения нити равная силе тяжести \(m_2g\) и сила натяжения нити, действующая вверх, равная \(Mg\) \[m_1g \sin \alpha \cdot AB+ m_2g \sin \alpha \cdot AC = Mg\sin (180-\alpha-\beta)\] Откуда \(AC\) \[AC=\dfrac{m_1g \sin \alpha \cdot AB}{Mg\sin (\alpha+\beta)-m_2g \sin \alpha}=\dfrac{0,1 \text{ кг}\cdot 10\text{ Н/кг}\cdot \sin 45^\circ\cdot 25\text{ см}}{0,2\text{ кг}\cdot 10\text{ Н/кг}\cdot \sin 60^\circ-0,2\text{ кг}\cdot 10\text{ Н/кг}\cdot \sin 45^\circ}\approx 55,6\text{ см}\]
Гладкий цилиндр лежит между двумя плоскостями, одна из которых вертикальна, а линия их пересечения горизонтальна (см. рисунок). Сила давления цилиндра на вертикальную стенку в \(n=\sqrt{3}\) раза превышает силу тяжести, действующую на цилиндр. Найдите угол \(\alpha\) между плоскостями. Сделайте рисунок, на котором укажите силы, действующие на цилиндр.
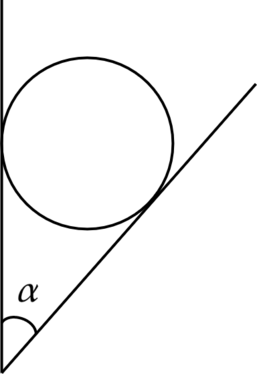
“Досрочная волна 2020 вариант 1”
Сделаем рисунок 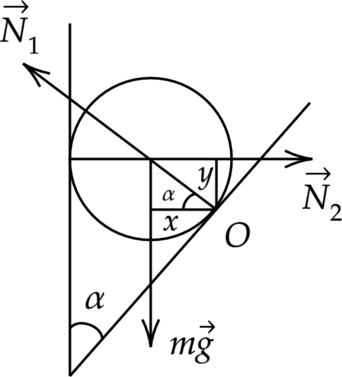
По третьему закону Ньютона, на вертикальную стенку действует цилиндр с силой \(\sqrt{3}mg\), значит, стенка действует с такой же силой на цилиндр Запишем второй закон Ньютона, с учетом покоя тела \[\vec{N_1}+\vec{N_2}+\vec{mg}=0\] Найдем тангенс угла \(\alpha\) \[tg \alpha =\dfrac{mg}{N_2}= \dfrac{mg}{mg\sqrt{3}}=\dfrac{1}{\sqrt{3}}\] Значит, угол равен \(30^\circ\)
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см\(^2\). В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой \(T\). Если нить перерезать, то шар всплывёт, а уровень воды изменится на \(h\) = 5 см. Найдите силу натяжения нити \(T\).
“Демоверсия 2018”
Пусть \(\rho\) – плотность жидкости, \(H\) – первоначальный уровень воды, тогда после перерезания нити уровень уменьшится на \(h\). Значит гидростатическое давление до перерезания нити \[P_1=\rho g H\] но так как есть еще сила натяжения нити, которая удерживает шар в воде, но не действует на дно, то сила давления на дно равна \[F_1=\rho \cdot g \cdot H \cdot S -T\] Во втором случае нить обрывается и шар всплывает и уровень уменьшается на \(h\), тогда сила давления на дно будет равна \[F_2=\rho \cdot g \cdot (H-h)\cdot S\] Поскольку масса щара и воды остается неизменным, то и сила давления на дно при равновесных состояниях остается неизменной, а значит мы можем приравнять \(F_1\) и \(F_2\) \[\rho \cdot g \cdot H \cdot S -T=\rho \cdot g\cdot H \cdot S -\rho \cdot g\cdot h \cdot S\] Выразим силу натяжения нити \[T=\rho \cdot g\cdot h \cdot S=1000 \text{ кг/м$^3$}\cdot 10\text{ Н/кг} \cdot 0,05\text{ м}\cdot 0,01\text{ м$^2$}=5\text{ Н}\]
Невесомый стержень АВ с двумя малыми грузиками массами \(m_1 = 200\) г и \(m_2 = 100\) г, расположенными в точках \(C\) и \(B\) соответственно, шарнирно закреплён в точке \(A\). Груз массой \(M = 100\) г подвешен к невесомому блоку за невесомую и нерастяжимую нить, другой конец которой соединён с нижним концом стержня, как показано на рисунке. Вся система находится в равновесии, если стержень отклонён от вертикали на угол \(\alpha=30^\circ\), а нить составляет угол с вертикалью, равный \(\beta =30^\circ\). Расстояние \(АС = b =\) 25 см. Определите длину \(l\) стержня \(АВ\). Сделайте рисунок с указанием сил, действующих на груз \(M\) и стержень.

“Демоверсия 2021”
Сделаем рисунок с указанием всех сил 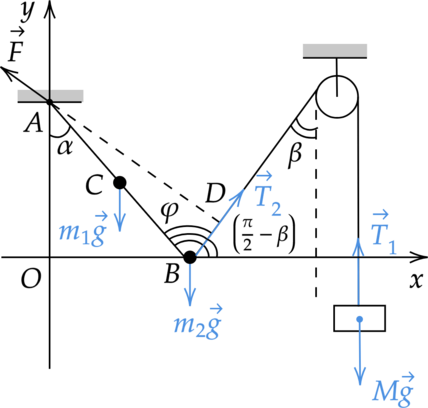
Запишем правило моментов относительно точки А. В точке \(B\) действует только сила натяжения нити равная силе тяжести \(m_1g\), в точке \(C\) действует вниз сила натяжения нити равная силе тяжести \(m_2g\) и сила натяжения нити, действующая вверх, равная \(Mg\) \[m_1g \sin \alpha \cdot b+ m_2g \sin \alpha \cdot l = Mg\sin (180-\alpha-\beta)\cdot l\] Откуда \(l\) \[l=\dfrac{m_1g \sin \alpha \cdot b}{Mg\sin (\alpha+\beta)-m_2g \sin \alpha}=\dfrac{0,2 \text{ кг}\cdot \sin 30^\circ\cdot 25\text{ см}}{0,1\text{ кг}\cdot \sin 60^\circ-0,1\text{ кг}\cdot \sin 30^\circ\cdot 25\text{ см}}\approx 68,3\text{ см}\]
В сосуд с привязанным нитью ко дну деревянным шариком наливают воду так, что шарик частично погружается под воду, а нить натягивается и действует на шарик с силой \(T = 7\) H. Насколько изменится уровень воды в сосуде после перерезания нити? Площадь дна сосуда \(S=100\) см\(^2\).
“Досрочная волна 2019 вариант 2”
Поскольку масса воды и шарика неизменна, то сила давления на дно сосуда одинакова в двух случаях: \[\rho g h_1S -T =\rho g h_2S \Rightarrow \rho g S \Delta h =T \Rightarrow \Delta h=\dfrac{T}{\rho g S}=\dfrac{7\text{ Н}}{1000\text{ кг/м$^3$}\cdot 10\text{ Н/кг}\cdot 10^{-2}\text{ м$^2$} }=0,07\text{ м}\]
На земле лежит бревно объемом \(V=0,3\) м\(^3\) и средней плотностью \(\rho=450 \) кг/м\(^3\). Чтобы поднять один край бревна надо приложить силу \(F_1=350\) Н. Найдите силу, которую надо приложить к другому краю, чтобы поднять его? Ответ дайте в Ньютонах.
Пусть центр тяжести находится на расстоянии \(x\) от края, к которому была приложена сила \(F_1\), а длина бревна равна \(l\). Также найдем массу бревна \(m=\rho V=450\text{ кг/м$^3$}\cdot 0,3\text{ м$^3$}=135\text{ кг}\).
Запишем уравнение моментов относительно центра тяжести (точка \(x\)) \[\begin{cases}
F_1l-mg(l-x)=0\\
F_2l-mgx=0\\
\end{cases}\] Сложим два уравнения \[l(F_1+F_1)-mgl+mgx-mgx=0 \Rightarrow l(F_1+F_2)=mgl\] Поделим на \(l\) и выразим \(F_2\) \[F_2=mg-F_1=135\text{ кг}\cdot 10\text{ Н/кг}-350\text{ Н}=1000\text{ Н}\]
В сосуд с водой вставлена труба с поперечным сечением \(S=10\) см\(^2\). В трубу налили \(m=100\) г масло плотностью 800 кг/м\(^3\). Найдите разность высот между жидкостью и водой. Ответ дайте в см.
Так как масло “легче” воды, то она будет сверху в трубе, а воды будет общей жидкостью для двух сообщающихся сосудов.
Приравняем давление внутри трубки и вне ее. \[\rho_\text{ м}g h_\text{ м}+ p_o=\rho_\text{ в}g h_\text{ в}+p_o\] где \(\rho_\text{ м}\) – плотность масла, \(\rho_\text{ в}\) – плотность воды, \(h_\text{ м}\) – высота столба масла, \(h_\text{ в}\) – высота столба воды, \(p_o\) – атмосферное давление.
Высоту столба жидкостей выразим через массу масла. \[h_\text{ м}=\dfrac{m}{\rho_\text{ м}\cdot S} \hspace{10 mm} h_\text{ в}=\dfrac{m}{\rho_\text{ в}\cdot S}\] Разность высот \[\Delta h= h_\text{ м}-h_\text{ в}=\dfrac{m}{S}\left(\dfrac{1}{\rho_\text{ м}}-\dfrac{1}{\rho_\text{ в}}\right)=\dfrac{0,1\text{ кг}}{0,001\text{ м$^2$}}\left(\dfrac{1}{800\text{ кг/м$^3$}}-\dfrac{1}{1000\text{ кг/м$^3$}}\right)=0,025\text{ м}=2,5\text{ см}\]



