Механическое равновесие (страница 2)
Готовиться с нами - ЛЕГКО!

К стенке стакана с водой привязан алюминиевый шар массой \(m=3\) кг. Нить образует со стенкой сосуда угол \(\alpha=30^\circ\). Найдите силу натяжения нити. Ответ дайте в Ньютонах. 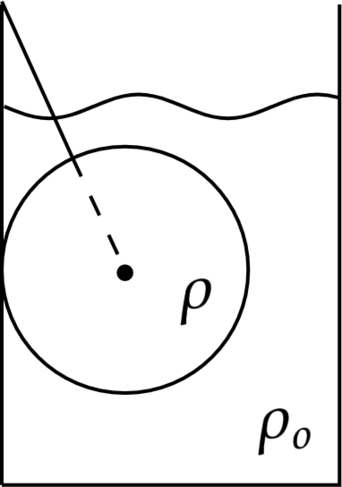
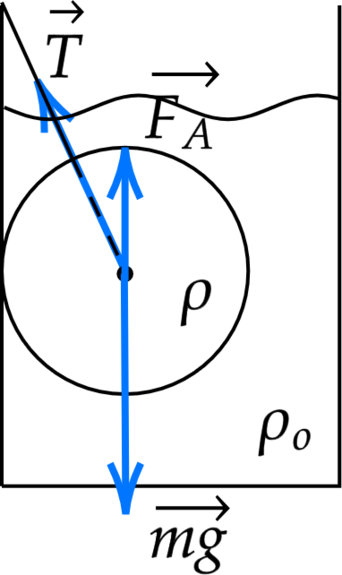 Запишем второй закон Ньютона на ось \(y\) \[F_\text{ А}-mg +T\cos \alpha =0 \quad (1)\] С учетом того, что сила Архимеда равна \[F_\text{ А} = \rho_0 g V=\rho_0 g \dfrac{m}{\rho} \quad (2)\] \(\rho_0\) – плотность жидкости, \(V\) – объем погруженной части тела, \(\rho\) – плотность алюминия.
Запишем второй закон Ньютона на ось \(y\) \[F_\text{ А}-mg +T\cos \alpha =0 \quad (1)\] С учетом того, что сила Архимеда равна \[F_\text{ А} = \rho_0 g V=\rho_0 g \dfrac{m}{\rho} \quad (2)\] \(\rho_0\) – плотность жидкости, \(V\) – объем погруженной части тела, \(\rho\) – плотность алюминия.
Выразим из (1) силу натяжения нити \(T\), с учетом (2) \[T=\dfrac{mg-\dfrac{\rho_0 g m}{\rho}}{\cos \alpha }=\dfrac{mg(\rho -\rho_0)}{\rho\cos \alpha }=\dfrac{30\text{ Н}(2700 \text{ кг/м$^3$}-1000\text{ кг/м$^3$})}{2700 \text{ кг/м$^3$}\cdot \dfrac{\sqrt{3}}{2}}=22\text{ Н}\]
Ко дну сосуда с водой площадью \(S=100\) см\(^2\) привязан деревянный шар, при этом нить натягивается и действует на шар с силой \(T\). Если перерезать нить, то шар всплывет, а уровень жидкости изменится на \(h=20\) см. Найдите силу натяжения нити. Ответ дайте в Н.
Пусть \(\rho\) – плотность жидкости, \(H\) – первоначальный уровень воды, тогда после перерезания нити уровень уменьшится на \(h\). Значит гидростатическое давление до перерезания нити \[P_1=\rho g H\] но так как есть еще сила натяжения нити, которая удерживает шар в воде, но не действует на дно, то сила давления на дно равна \[F_1=\rho \cdot g \cdot H \cdot S -T\] Во втором случае нить обрывается и шар всплывает и уровень уменьшается на \(h\), тогда сила давления на дно будет равна \[F_2=\rho \cdot g \cdot (H-h)\cdot S\] Поскольку масса щара и воды остается неизменным, то и сила давления на дно при равновесных состояниях остается неизменной, а значит мы можем приравнять \(F_1\) и \(F_2\) \[\rho \cdot g \cdot H \cdot S -T=\rho \cdot g\cdot H \cdot S -\rho \cdot g\cdot h \cdot S\] Выразим силу натяжения нити \[T=\rho \cdot g\cdot h \cdot S=1000 \text{ кг/м$^3$}\cdot 10\text{ Н/кг} \cdot 0,2\text{ м}\cdot 0,01\text{ м$^2$}=20\text{ Н}\]
Стержень согнули под прямым углом с соотношением полученных сторон 2:3 и подвесили нить, привязанную к точке сгиба. Найдите массу груза, который надо прикрепить к концу короткой стороны, чтобы концы сторон находились на одном уровне, если масса стержня 600 г. Ответ дайте в граммах.
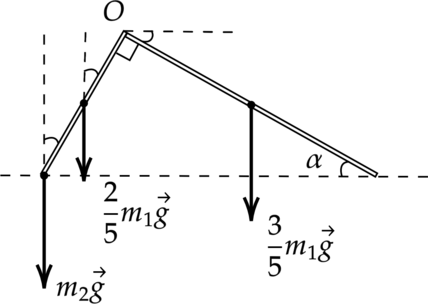 Запишем правило моментов относительно оси подвеса. \[\dfrac{3}{5}m_1g \dfrac{3l}{10}\cos \alpha -\dfrac{2}{5}m_1g\dfrac{l}{5}\sin \alpha - m_2 \dfrac{2l}{5}\cos \alpha =0\] где \(l\) – длина стержня, \(m_1\) – его масса. (Здесь берется \(\dfrac{3l}{10}\) в первом случае, так как центр тяжести однородного стержня находится в середине, а у нас эта сторона равна \(\dfrac{3l}{5}\), а половина \(\dfrac{3l}{10}\), точно также и для второго слагаемого) Выразим отсюда массу грузика \[m_2=\dfrac{m_1}{20}(9ctg \alpha -4)\] так как отношение сторон 2:3, то \(ctg \alpha =1,5\) А значит \[m_2=\dfrac{9,5m_1}{20}=285\text{ г}\]
Запишем правило моментов относительно оси подвеса. \[\dfrac{3}{5}m_1g \dfrac{3l}{10}\cos \alpha -\dfrac{2}{5}m_1g\dfrac{l}{5}\sin \alpha - m_2 \dfrac{2l}{5}\cos \alpha =0\] где \(l\) – длина стержня, \(m_1\) – его масса. (Здесь берется \(\dfrac{3l}{10}\) в первом случае, так как центр тяжести однородного стержня находится в середине, а у нас эта сторона равна \(\dfrac{3l}{5}\), а половина \(\dfrac{3l}{10}\), точно также и для второго слагаемого) Выразим отсюда массу грузика \[m_2=\dfrac{m_1}{20}(9ctg \alpha -4)\] так как отношение сторон 2:3, то \(ctg \alpha =1,5\) А значит \[m_2=\dfrac{9,5m_1}{20}=285\text{ г}\]
К вертикальной стенке прислонена однородная доска, образующая с горизонтальным полом угол \(\alpha=45^\circ\) Коэффициент трения доски об пол равен \(\mu=0,4\) Каков должен быть коэффициент трения доски о стену, чтобы доска оставалась в равновесии?
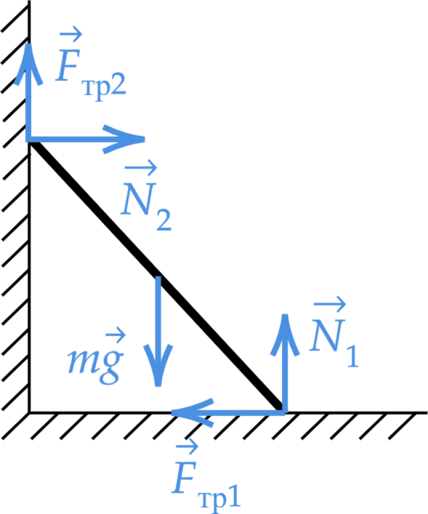 Запишем второй закон Ньютона и правило моментов относительно центра доски, с учетом того, что доска покоится \[\begin{cases}
mg-N_1-F_\text{ тр2}=0\\
N_2-F_\text{ тр1}=0 \quad (1)\\
(F_\text{ тр1}+ N_2 )\dfrac{l}{2}\sin \alpha + F_\text{ тр2}\dfrac{l}{2}\cos \alpha-N_1 \dfrac{l}{2}\cos \alpha =0 \quad (2)\\
\end{cases}\] Так как \(F_\text{ тр1}=\mu N_1\), а \(F_\text{ тр2}=\mu_2 N_2\) и с учетом (1) уравнение (2) можно переписать в виде \[2\mu N_1 \sin \alpha + \mu_2 \mu N_1 \cos \alpha =N_1 \cos \alpha\] Отсюда \(\mu_2\) \[\mu_2 =\dfrac{N_1 \cos \alpha - 2\mu N_1 \sin \alpha }{\mu N_1 \cos \alpha }=\dfrac{1}{\mu} -2 tg \alpha =\dfrac{1}{0,4}-2\cdot 1=0,5\]
Запишем второй закон Ньютона и правило моментов относительно центра доски, с учетом того, что доска покоится \[\begin{cases}
mg-N_1-F_\text{ тр2}=0\\
N_2-F_\text{ тр1}=0 \quad (1)\\
(F_\text{ тр1}+ N_2 )\dfrac{l}{2}\sin \alpha + F_\text{ тр2}\dfrac{l}{2}\cos \alpha-N_1 \dfrac{l}{2}\cos \alpha =0 \quad (2)\\
\end{cases}\] Так как \(F_\text{ тр1}=\mu N_1\), а \(F_\text{ тр2}=\mu_2 N_2\) и с учетом (1) уравнение (2) можно переписать в виде \[2\mu N_1 \sin \alpha + \mu_2 \mu N_1 \cos \alpha =N_1 \cos \alpha\] Отсюда \(\mu_2\) \[\mu_2 =\dfrac{N_1 \cos \alpha - 2\mu N_1 \sin \alpha }{\mu N_1 \cos \alpha }=\dfrac{1}{\mu} -2 tg \alpha =\dfrac{1}{0,4}-2\cdot 1=0,5\]
Два небольших шара массами \(m_1 = 0,2\) кг и \(m_2 = 0,3\) кг закреплены на концах невесомого стержня \(AB\), расположенного горизонтально на опорах \(C \)и \(D\) (см. рисунок). Расстояние между опорами \(l = 0,6\) м, а расстояние \(AC\) равно 0,2 м. Чему равна длина стержня \(L\), если сила давления стержня на опору \(D\) в 2 раза больше, чем на опору \(C\)? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень — шары».
Источник: Демонстрационная версия ЕГЭ – 2020 по физике. 
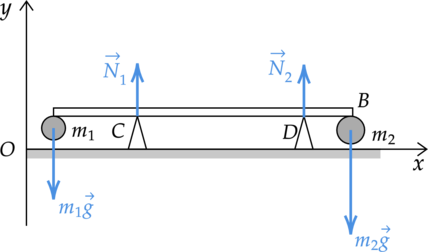 На твердое тело, образованное двумя шарами и стержнем действует силы тяжести первого и второго шаров \(m_1 g\)и \(m_2g\), а также силы реакции опоры \(N_1\) и \(N_2\). По условию \(2N_1=N_2\) Запишем второй закон Ньютона и правило моментов относительно точки А. \[\begin{cases}
N_1 +N_2 -m_1g -m_2 g=0\\
N_1 x +N_2 (l+x)-m_2 g L=0\\
\end{cases}\] где \(x\) – AC и плечо силы \(N_1\). Так как \(N_2=2N_1\), то систему уравнений можно переписать в виде \[\begin{cases}
3N_1 =g(m_1 +m_2)\\
N_1 x +2N_1 (l+x)=m_2 g L\\
\end{cases}\] Поделим второе уравнение на первое \[x+\dfrac{2l}{3}=L\dfrac{m_2}{m_1+m_2}\] Отсюда длина стержня \[L=\dfrac{m_2+m_1}{m_2}\left(x+\dfrac{2l}{3}\right)=\dfrac{0,3\text{ кг}+0,2\text{ кг}}{0,3\text{ кг}}\left(0,2\text{ м}+ \dfrac{2\cdot 0,6 \text{ м}}{3}\right)=1\text{ м}\]
На твердое тело, образованное двумя шарами и стержнем действует силы тяжести первого и второго шаров \(m_1 g\)и \(m_2g\), а также силы реакции опоры \(N_1\) и \(N_2\). По условию \(2N_1=N_2\) Запишем второй закон Ньютона и правило моментов относительно точки А. \[\begin{cases}
N_1 +N_2 -m_1g -m_2 g=0\\
N_1 x +N_2 (l+x)-m_2 g L=0\\
\end{cases}\] где \(x\) – AC и плечо силы \(N_1\). Так как \(N_2=2N_1\), то систему уравнений можно переписать в виде \[\begin{cases}
3N_1 =g(m_1 +m_2)\\
N_1 x +2N_1 (l+x)=m_2 g L\\
\end{cases}\] Поделим второе уравнение на первое \[x+\dfrac{2l}{3}=L\dfrac{m_2}{m_1+m_2}\] Отсюда длина стержня \[L=\dfrac{m_2+m_1}{m_2}\left(x+\dfrac{2l}{3}\right)=\dfrac{0,3\text{ кг}+0,2\text{ кг}}{0,3\text{ кг}}\left(0,2\text{ м}+ \dfrac{2\cdot 0,6 \text{ м}}{3}\right)=1\text{ м}\]
Вертикальная труба с поршнем, плотно прилегающим к ее внутренним стенкам, опущена нижним концом в воду. Вначале поршень находился в самом нижнем положении, на уровне воды, а затем его медленно поднимают на высоту 20 м. Пренебрегая трением, найдите совершенную при этом работу (в кДж). Площадь поршня 100 см\(^2\). Атмосферное давление 100 кПа.
Процесс поднятия поршня происходит в 2 этапа. Первый этап: давление под поршнем будет положительным и равное \[p_0-\rho g h\] где \(\rho\) – плотность воды, \(h\) – высота подъезда поршня.
Вода будет заполнять весь объем под поршнем, а приложенная к поршню сила будет компенсировать давление внутри, она будет равна \[F=\rho g h S\] Она будет линейно возрастать. Это будет до момента, пока вода не поднимется на высоту, равную \[h_0=\dfrac{p_0}{\rho g}=\dfrac{100\text{ кПа}}{1000\text{ кг/м$^3$} \cdot 10 Н/кг}=10\text{ м}\] При подъеме поршня на высоту \(h_0\) давление станет равным нулю. После этого вода перестает подниматься, а сила, приложенная к поршню, остается равной \[F'=\rho g h_0 S=p_0S\] Работа по поднятию равна сумме работ: работе по поднятию до высоты \(h_0\) \(A_0=\dfrac{0+F_1}{2}h_0=\dfrac{p_o S h_0}{2}\) (так как она линейно возрастает, то берем как среднее арифметическое от начального, до конечного) и работе по поднятию от высоты \(h_0\) и конечной высоты \(A_1=F_1(h_1-h_0)=p_o Sh_1-p_o Sh_0\). Значит, полная работа равна \[A=\dfrac{p_o S h_0}{2}+ p_0 S h_1 -p_0 Sh_0=p_0 S \left(h_1 -\dfrac{h_0}{2})=100\text{ кПа}\cdot 10^{-2}\text{ м$^2$}(20\text{ м}-5\text{ м}\right)=15\text{ кДж}\]
На границе раздела двух жидкостей плотностями \(\rho_1=1500\) и \(\rho_2=1000\) плавает щарик. Какая должна быть плотность шарика \(\rho\), чтобы над границей раздела жидкостей находилось 25% объема шарика. Ответ дайте в кг/м\(^3\) 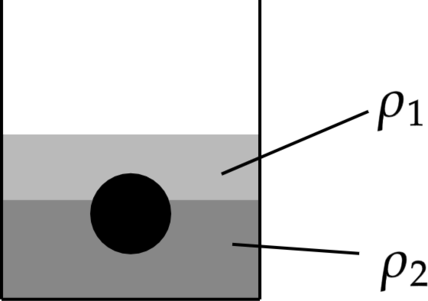
Так как шарик неподвижен, то из второго закона Ньютона сила Архимеда должна уравновешивать силу тяжести. \[\rho_1 g V_1 +\rho_2 g V_2 =\rho g (v_1 +V_2)\quad (1)\] где \(V_1\) и \(V_2\) – объемы шарика, находящиеся над и под границей раздела жидкостей. Так как по условию над границей раздела двух жидкостей должно находится 25 % объема, то \[\dfrac{V_1}{V_1+V_2}=\dfrac{1}{4} \Rightarrow \dfrac{V_2}{V_1+V_2}=1-\dfrac{1}{4}=\dfrac{3}{4}\quad (2)\] Разделим (1) на \((V_1+V_2) g\) и получим \[\rho_1 \dfrac{V_1}{V_1+V_2}+\rho_2 \dfrac{V_2}{V_1+V_2}=\rho \quad (3)\] С учетом (2) уравнение (3) можно переписать в виде \[\rho =\dfrac{\rho_1}{4}+\dfrac{3\rho_2}{4}=\dfrac{1500\text{ кг/м$^3$}}{4}+\dfrac{3 \cdot 1000\text{ кг/м$^3$}}{4}=1125\text{ кг/м$^3$}\]



